Stanford Pratical Machine Learning-Bagging

这一章主要介绍Bagging和相关的知识，本质就是一种训练多个模型，然后去做决策和平均的策略和算法。主要目的是通过多个模型的决策结果来减少方差。不稳定模型 -> 稳定模型。

Bagging - Bootstrap AGGregatING

这些模型的训练是独立的，可并行的昂！！！

• Learn n base learners in parallel, combine to reduce model variance
• Each base learner is trained on a bootstrap sample
  • Given a dataset of m examples, create a sample by randomly sampling m examples with replacement
  • Around $1-1/e\approx 63$ unique examples will be sampled use the out-of-bag examples for validation
• Combine learners by averaging the outputs (regression) or majority voting (classification)
• Random forest: bagging with decision trees
  • usually select random subset of features for each bootstrap sample

Bagging Code (scikit-learn)

• Code

class Bagging:
	def __init__(self, base_learner, n_learners):
		self.learners = [clone(base_learner) for _ in range(n_learners)]

	def fit(self, X, y):
		for learner in self.learners:
			examples = np.random.choice(
				np.arange(len(X)), int(len(X)), replace=True)
			learner.fit(X.iloc[examples, :], y.iloc[examples])
      
	def predict(self, X):
		preds = [learner.predict(X) for learner in self.learners]
		return np.array(preds).mean(axis=0) 
PYTHON

Random Forest

• A case of bagging, use decision tree as the base learner
• Ofter randomly select a subset of features for each learner

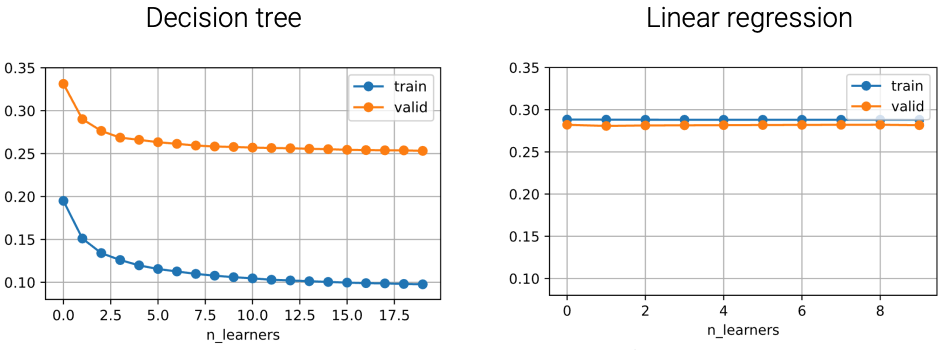
Apply bagging with unstable Learners

方差比较大的模型，被我们称为unstable模型。

• Bagging reduces model variance, especially for unstable learners
• Given ground truth $$ and a set of base learners $$, for regression, bagging prediction: $$
• Given $$, we have

$$

$$ is with bagging, $$ is single learner.

Unstable Learners

• Decision tree is unstable, linear regression is stable

image-20230826095859527

References

1. slides