Stanford Pratical Machine Learning-决策树

这一章主要介绍决策树，Decision Trees用的很广泛啦！！！

Decision Trees

• Explainable
• Handle both numerical and categorical features without preprocessing

• Pros
  • explainable
  • can handle both numerical and categorical features
• Cons
  • very non-robust(ensemble to help)
  • complex trees cause overfitting(prune trees)
  • not easy to parellelized in computing

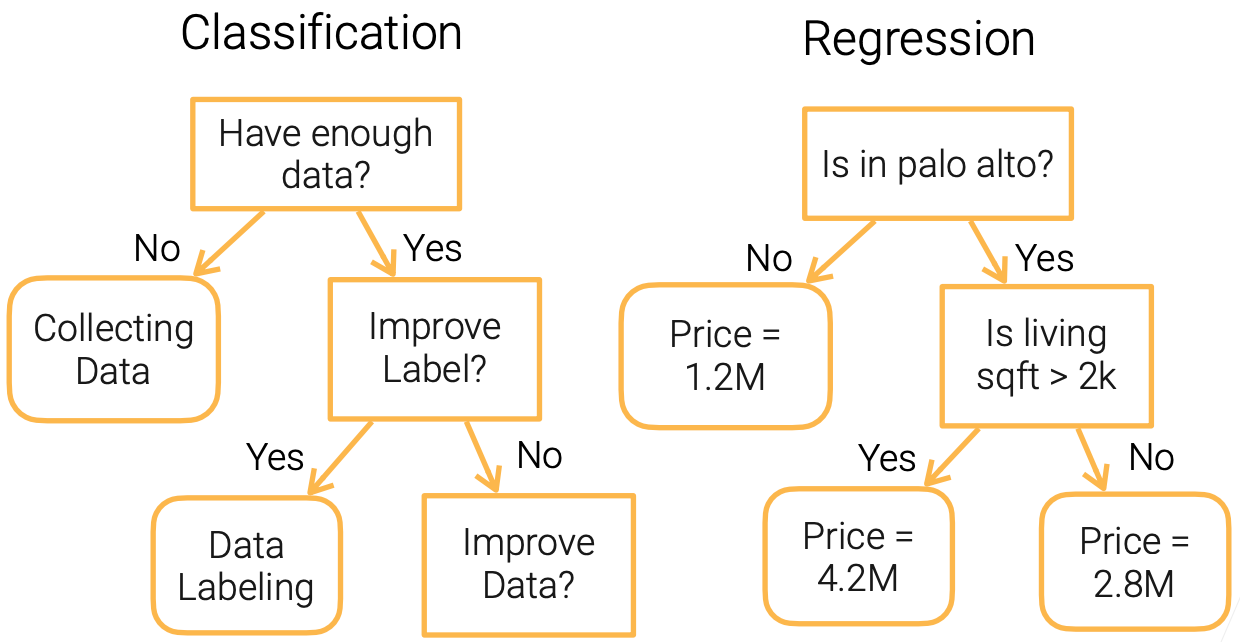
Building Decision Trees

• Use a top-down approach, staring from the root node with the set of all features
• At each parent node, pick a feature to split the examples
  • Feature selection criteria
    • Maximize variance reduction for continuous target
    • Maximize Information gain (1 - entropy) for categorical target
    • Maximize $Gini\ impurity\ = 1 - \sum_{i=1}^{n} p_{i}^{2}$ for categorical target
  • All examples are used for feature selection at each node

Limitations of decision Trees

• Over-complex trees can overfit the data
  • Limit the number of levels of splitting
  • Prune branches
• Sensitive to data
  • Changing a few examples can cause picking different features that lead to a different tree
  • Random forest
• Not easy to be parallelized in computing

Random Forest

• Train multiple decision trees to improve robustness
  • Trees are trained independently in parallel
  • Majority voting for classification, average for regression
• Where is the randomness from?
  • Bagging: randomly sample training examples with replacement
    • E.g. [1,2,3,4,5] [1,2,2,3,4]
  • Randomly select a subset of features

Gradient Boosting Decision Trees

对于之前预测不准的结果，再来一棵树进行补充处理！

• Train multiple trees sequentially
• At step t = 1…, denote by $F_t(x)$ the sum of past trained trees
  • Train a new tree $f_t$ on residuals: ${(x_i, y_i - F_t(x_i)}_{i = 1, \dots}$
  • $F_{t+1}(x) = F_t(x) + f_t(x)$
• Тhе rеѕіduаl еquаlѕ tо $-\part{L}/\part{F}$ іf uѕіng mеаn ѕquаrе error as the loss, so it’s called gradient boosting.

Summary

• Decision tree: an explainable model for classification/regression
• Ensemble trees to reduce bias and variance
  • Random forest: trees trained in parallel with randomness
  • Gradient boosting trees: train in sequential on residuals
• Trees are widely used in industry
  • Simple, easy-to-tune, often gives satisfied results

References

1. slides