D2L-10-Modern Recurrent Neural Networks

本文最后更新于：1 年前

循环神经网络在实践中一个常见问题是数值不稳定性。 尽管我们已经应用了梯度裁剪等技巧来缓解这个问题， 但是仍需要通过设计更复杂的序列模型来进一步处理它。 具体来说，我们将引入两个广泛使用的网络， 即门控循环单元（gated recurrent units，GRU）和 长短期记忆网络（long short-term memory，LSTM）。 然后，我们将基于一个单向隐藏层来扩展循环神经网络架构。 我们将描述具有多个隐藏层的深层架构， 并讨论基于前向和后向循环计算的双向设计。 现代循环网络经常采用这种扩展。 在解释这些循环神经网络的变体时， 我们将继续考虑 8节中的语言建模问题。

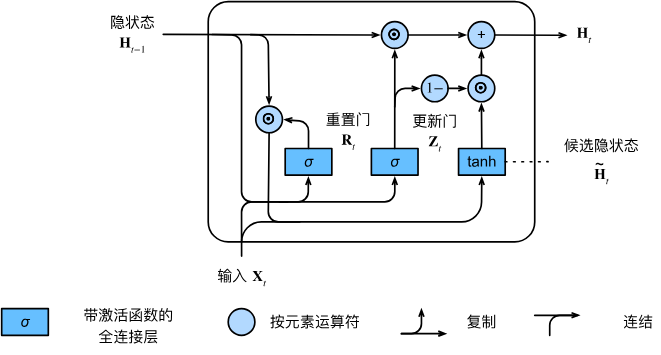
门控循环单元（GRU）

门控隐状态

重置门和更新门

  • 重置门（reset gate）和更新门（update gate）。 我们把它们设计成(0,1)区间中的向量， 这样我们就可以进行凸组合。 重置门允许我们控制“可能还想记住”的过去状态的数量； 更新门将允许我们控制新状态中有多少个是旧状态的副本。输入是由当前时间步的输入和前一时间步的隐状态给出。 两个门的输出是由使用sigmoid激活函数的两个全连接层给出。

../_images/gru-1.svg
$$
\begin{split}\begin{aligned}
\mathbf{R}t = \sigma(\mathbf{X}t \mathbf{W}{xr} + \mathbf{H}{t-1} \mathbf{W}_{hr} + \mathbf{b}r),\
\mathbf{Z}t = \sigma(\mathbf{X}t \mathbf{W}{xz} + \mathbf{H}{t-1} \mathbf{W}{hz} + \mathbf{b}_z),
\end{aligned}\end{split}
$$

候选隐状态

  • 我们将重置门$\mathbf{R}_t$与 (8.4.5) 中的常规隐状态更新机制集成， 得到在时间步t的候选隐状态（candidate hidden state）$\tilde{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$

$$
\tilde{\mathbf{H}}t = \tanh(\mathbf{X}t \mathbf{W}{xh} + \left(\mathbf{R}t \odot \mathbf{H}{t-1}\right) \mathbf{W}{hh} + \mathbf{b}_h),
$$

其中$\mathbf{W}{xh} \in \mathbb{R}^{d \times h}$和$\mathbf{W}{hh} \in \mathbb{R}^{h \times h}$是权重参数， $\mathbf{b}_h \in \mathbb{R}^{1 \times h}$是偏置项， 符号$\odot$是Hadamard积（按元素乘积）运算符。 在这里，我们使用tanh非线性激活函数来确保候选隐状态中的值保持在区间(−1,1)中。$\mathbf{R}t$和$\mathbf{H}{t-1}$的元素相乘可以减少以往状态的影响。 每当重置门$\mathbf{R}_t$中的项接近1时， 我们恢复一个如 (8.4.5)中的普通的循环神经网络。 对于重置门$\mathbf{R}_t$中所有接近0的项， 候选隐状态是以$\mathbf{X}_t$作为输入的多层感知机的结果。 因此，任何预先存在的隐状态都会被重置为默认值。

../_images/gru-2.svg

隐状态

  • 上述的计算结果只是候选隐状态，我们仍然需要结合更新门$\mathbf{Z}_t$的效果。 这一步确定新的隐状态$\mathbf{H}t \in \mathbb{R}^{n \times h}$在多大程度上来自旧的状态$\mathbf{H}{t-1}$和新的候选状态$\tilde{\mathbf{H}}_t$。 更新门$\mathbf{Z}t$仅需要在$\mathbf{H}{t-1}$和$\tilde{\mathbf{H}}_t$之间进行按元素的凸组合就可以实现这个目标。 这就得出了门控循环单元的最终更新公式：

$$
\mathbf{H}_t = \mathbf{Z}t \odot \mathbf{H}{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t.
$$

每当更新门$\mathbf{Z}_t$接近1时，模型就倾向只保留旧状态。 此时，来自$\mathbf{X}_t$的信息基本上被忽略， 从而有效地跳过了依赖链条中的时间步t。 相反，当$\mathbf{Z}_t$接近0时， 新的隐状态$\mathbf{H}_t$就会接近候选隐状态$\tilde{\mathbf{H}}_t$。 这些设计可以帮助我们处理循环神经网络中的梯度消失问题， 并更好地捕获时间步距离很长的序列的依赖关系。 例如，如果整个子序列的所有时间步的更新门都接近于1， 则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。

image-20230814205122506

从零开始实现

  • Dependencies
1
2
3
4
5
6
import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

初始化模型参数

  • 下一步是初始化模型参数。 我们从标准差为0.01的高斯分布中提取权重， 并将偏置项设为0，超参数num_hiddens定义隐藏单元的数量， 实例化与更新门、重置门、候选隐状态和输出层相关的所有权重和偏置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xz, W_hz, b_z = three()  # 更新门参数
    W_xr, W_hr, b_r = three()  # 重置门参数
    W_xh, W_hh, b_h = three()  # 候选隐状态参数
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

定义模型

  • 现在我们将定义隐状态的初始化函数init_gru_state。 与 8.5节中定义的init_rnn_state函数一样， 此函数返回一个形状为（批量大小，隐藏单元个数）的张量，张量的值全部为零。
1
2
def init_gru_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )
  • 现在我们准备定义门控循环单元模型， 模型的架构与基本的循环神经网络单元是相同的， 只是权重更新公式更为复杂。
1
2
3
4
5
6
7
8
9
10
11
12
def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

训练与预测

  • 训练和预测的工作方式与 8.5节完全相同。 训练结束后，我们分别打印输出训练集的困惑度， 以及前缀“time traveler”和“traveler”的预测序列上的困惑度。
1
2
3
4
5
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
                            init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

简洁实现

  • 高级API包含了前文介绍的所有配置细节， 所以我们可以直接实例化门控循环单元模型。 这段代码的运行速度要快得多， 因为它使用的是编译好的运算符而不是Python来处理之前阐述的许多细节。
1
2
3
4
5
num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

长短期记忆网络（LSTM）

隐变量模型存在着长期信息保存和短期输入缺失的问题。 解决这一问题的最早方法之一是长短期存储器（long short-term memory，LSTM）

门控记忆元

输入门、忘记门和输出门

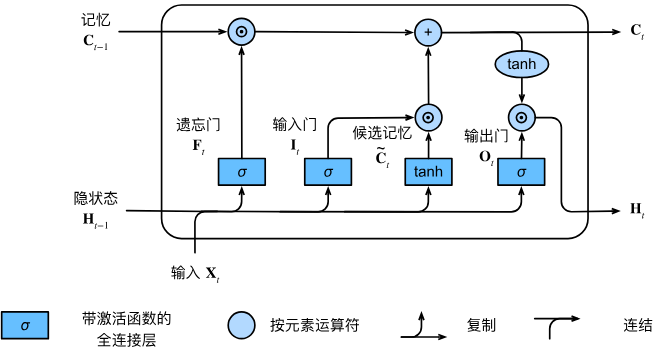
  • 长短期记忆网络的设计灵感来自于计算机的逻辑门。 长短期记忆网络引入了记忆元（memory cell），或简称为单元（cell）。 有些文献认为记忆元是隐状态的一种特殊类型， 它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。 为了控制记忆元，我们需要许多门。 其中一个门用来从单元中输出条目，我们将其称为输出门（output gate）。 另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate）。 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate）来管理， 这种设计的动机与门控循环单元相同， 能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。 让我们看看这在实践中是如何运作的。
  • 由三个具有sigmoid激活函数的全连接层处理， 以计算输入门、遗忘门和输出门的值。 因此，这三个门的值都在(0,1)的范围内。

../_images/lstm-0.svg

  • 细化一下长短期记忆网络的数学表达。 假设有h个隐藏单元，批量大小为n，输入数为d。 因此，输入为$\mathbf{X}t \in \mathbb{R}^{n \times d}$， 前一时间步的隐状态为$\mathbf{H}{t-1} \in \mathbb{R}^{n \times h}$。 相应地，时间步t的门被定义如下： 输入门是$\mathbf{I}_t \in \mathbb{R}^{n \times h}$， 遗忘门是$\mathbf{F}_t \in \mathbb{R}^{n \times h}$， 输出门是$\mathbf{O}_t \in \mathbb{R}^{n \times h}$。 它们的计算方法如下：

$$
\begin{split}\begin{aligned}
\mathbf{I}t &= \sigma(\mathbf{X}t \mathbf{W}{xi} + \mathbf{H}{t-1} \mathbf{W}_{hi} + \mathbf{b}i),\
\mathbf{F}t &= \sigma(\mathbf{X}t \mathbf{W}{xf} + \mathbf{H}{t-1} \mathbf{W}{hf} + \mathbf{b}f),\
\mathbf{O}t &= \sigma(\mathbf{X}t \mathbf{W}{xo} + \mathbf{H}{t-1} \mathbf{W}{ho} + \mathbf{b}_o),
\end{aligned}\end{split}
$$

其中$\mathbf{W}{xi}, \mathbf{W}{xf}, \mathbf{W}{xo} \in \mathbb{R}^{d \times h}$和$\mathbf{W}{hi}, \mathbf{W}{hf}, \mathbf{W}{ho} \in \mathbb{R}^{h \times h}$是权重参数， $\mathbf{b}_i, \mathbf{b}_f, \mathbf{b}_o \in \mathbb{R}^{1 \times h}$是偏置参数。

候选记忆元

  • 由于还没有指定各种门的操作，所以先介绍候选记忆元（candidate memory cell） $\tilde{\mathbf{C}}_t \in \mathbb{R}^{n \times h}$。 它的计算与上面描述的三个门的计算类似， 但是使用tanh函数作为激活函数，函数的值范围为(−1,1)。 下面导出在时间步t处的方程：

$$
\tilde{\mathbf{C}}t = \text{tanh}(\mathbf{X}t \mathbf{W}{xc} + \mathbf{H}{t-1} \mathbf{W}_{hc} + \mathbf{b}_c),
$$

其中$\mathbf{W}{xc} \in \mathbb{R}^{d \times h}$和$\mathbf{W}{hc} \in \mathbb{R}^{h \times h}$是权重参数，$\mathbf{b}_c \in \mathbb{R}^{1 \times h}$是偏置参数。

../_images/lstm-1.svg

记忆单元

  • 在门控循环单元中，有一种机制来控制输入和遗忘（或跳过）。 类似地，在长短期记忆网络中，也有两个门用于这样的目的： 输入门$\mathbf{I}_t$控制采用多少来自$\tilde{\mathbf{C}}_t$的新数据， 而遗忘门$\mathbf{F}t$控制保留多少过去的记忆元$\mathbf{C}{t-1} \in \mathbb{R}^{n \times h}$的内容。 使用按元素乘法，得出：

$$
\mathbf{C}_t = \mathbf{F}t \odot \mathbf{C}{t-1} + \mathbf{I}_t \odot \tilde{\mathbf{C}}_t.
$$

如果遗忘门始终为1且输入门始终为0， 则过去的记忆元$\mathbf{C}_{t-1}$将随时间被保存并传递到当前时间步。 引入这种设计是为了缓解梯度消失问题， 并更好地捕获序列中的长距离依赖关系。

../_images/lstm-2.svg

GRU是Z和1-Z，这里是F和I两个，就是说明两个都可以同时保留 or 去除

隐状态

  • 我们需要定义如何计算隐状态$\mathbf{H}_t \in \mathbb{R}^{n \times h}$，这就是输出门发挥作用的地方。 在长短期记忆网络中，它仅仅是记忆元的tanh的门控版本。 这就确保了$\mathbf{H}_t$的值始终在区间(−1,1)内：

$$
\mathbf{H}_t = \mathbf{O}_t \odot \tanh(\mathbf{C}_t).
$$

只要输出门接近1，我们就能够有效地将所有记忆信息传递给预测部分， 而对于输出门接近0，我们只保留记忆元内的所有信息，而不需要更新隐状态。

image-20230814214056174

从零开始实现

  • Dependencies:
1
2
3
4
5
6
import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

初始化模型参数

  • 我们需要定义和初始化模型参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def get_lstm_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xi, W_hi, b_i = three()  # 输入门参数
    W_xf, W_hf, b_f = three()  # 遗忘门参数
    W_xo, W_ho, b_o = three()  # 输出门参数
    W_xc, W_hc, b_c = three()  # 候选记忆元参数
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
              b_c, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

定义模型

  • 长短期记忆网络的隐状态需要返回一个额外的记忆元， 单元的值为0，形状为（批量大小，隐藏单元数）。 因此，我们得到以下的状态初始化。
1
2
3
def init_lstm_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device),
            torch.zeros((batch_size, num_hiddens), device=device))
  • 实际模型的定义与我们前面讨论的一样： 提供三个门和一个额外的记忆元。 请注意，只有隐状态才会传递到输出层， 而记忆元$\mathbf{C}_t$不直接参与输出计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
        F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
        O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
        C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * torch.tanh(C)
        Y = (H @ W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H, C)

训练和预测

1
2
3
4
5
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
                            init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

简洁实现

  • 使用高级API，我们可以直接实例化LSTM模型。
1
2
3
4
5
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

长短期记忆网络是典型的具有重要状态控制的隐变量自回归模型。 多年来已经提出了其许多变体，例如，多层、残差连接、不同类型的正则化。 然而，由于序列的长距离依赖性，训练长短期记忆网络 和其他序列模型（例如门控循环单元）的成本是相当高的。 在后面的内容中，我们将讲述更高级的替代模型，如Transformer。

深度循环神经网络

  • 循环神经网络更深！更多的非线性get！

../_images/deep-rnn.svg

原来是一个隐藏层，现在是多个隐藏层嘛。

函数依赖关系

  • 第一层以x作为输入，后面的隐藏层都以其前一隐藏层的内容作为输入。假设在时间步t有一个小批量的输入数据$\mathbf{X}_t \in \mathbb{R}^{n \times d}$（样本数：n，每个样本中的输入数：d）。 同时，将$l^\mathrm{th}$隐藏层$l=1,\ldots,L$的隐状态设为$\mathbf{H}_t^{(l)} \in \mathbb{R}^{n \times h}$（隐藏单元数：h）， 输出层变量设为$\mathbf{O}_t \in \mathbb{R}^{n \times q}$（输出数$q$）。 设置$\mathbf{H}_t^{(0)} = \mathbf{X}_t$， 第$l$个隐藏层的隐状态使用激活函数$\phi_l$，则：

$$
\mathbf{H}t^{(l)} = \phi_l(\mathbf{H}t^{(l-1)} \mathbf{W}{xh}^{(l)} + \mathbf{H}{t-1}^{(l)} \mathbf{W}_{hh}^{(l)} + \mathbf{b}_h^{(l)}),
$$

权重$\mathbf{W}{xh}^{(l)} \in \mathbb{R}^{h \times h}$，$\mathbf{W}{hh}^{(l)} \in \mathbb{R}^{h \times h}$和偏置$\mathbf{b}_h^{(l)} \in \mathbb{R}^{1 \times h}$都是第$l$个隐藏层的模型参数。

  • 最后，输出层的计算仅基于第$l$个隐藏层最终的隐状态：

$$
\mathbf{O}_t = \mathbf{H}t^{(L)} \mathbf{W}{hq} + \mathbf{b}_q,
$$

  • 总结：通过更多的隐藏层来获得更多的非线性性。

简洁实现

  • Dependencies
1
2
3
4
5
6
import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
  • 因为我们有不同的词元，所以输入和输出都选择相同数量，即vocab_size。 隐藏单元的数量仍然是256。 唯一的区别是，我们现在通过num_layers的值来设定隐藏层数。
1
2
3
4
5
6
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)

d2l.RNNModel里面加了一个输出层昂！因为nn.LSTM里面只有隐藏层，不带输出层，所以我们要手动带上一个输出层昂！！！

训练与预测

1
2
num_epochs, lr = 500, 2
d2l.train_ch8(model, train_iter, vocab, lr*1.0, num_epochs, device)

双向循环神经网络

  • 完形填空应用场景
    • 取决于过去和未来的上下文，可以填很不一样的词
    • 目前RNN只看过去
    • 在填空的时候，RNN应该看看未来

隐马尔可夫模型中的动态规划

../_images/hmm.svg

任何$h_t \to h_{t+1}$转移 都是由一些状态转移概率$P(h_{t+1} \mid h_{t})$给出。 这个概率图模型就是一个隐马尔可夫模型（hidden Markov model，HMM）

  • 对于有T个观测值的序列， 我们在观测状态和隐状态上具有以下联合概率分布：

$$
P(x_1, \ldots, x_T, h_1, \ldots, h_T) = \prod_{t=1}^T P(h_t \mid h_{t-1}) P(x_t \mid h_t), \text{ where } P(h_1 \mid h_0) = P(h_1).
$$

这里还有好多推导，累了，毁灭吧！看看原文吧orz，双向RNN D2L Website

双向模型

定义

../_images/birnn.svg

  • 组成部分：

    • 一个前向的RNN隐藏层
    • 一个反向的RNN隐藏层
    • 合并两个隐状态得到输出

  • 前向和反向隐状态的更新如下：

$$
\begin{split}\begin{aligned}
\overrightarrow{\mathbf{H}}t &= \phi(\mathbf{X}t \mathbf{W}{xh}^{(f)} + \overrightarrow{\mathbf{H}}{t-1} \mathbf{W}_{hh}^{(f)} + \mathbf{b}h^{(f)}),\
\overleftarrow{\mathbf{H}}t &= \phi(\mathbf{X}t \mathbf{W}{xh}^{(b)} + \overleftarrow{\mathbf{H}}{t+1} \mathbf{W}{hh}^{(b)} + \mathbf{b}_h^{(b)}), \
\mathbf{H}_t &= [\overrightarrow{\mathbf{H}}_t, \overleftarrow{\mathbf{H}}_t],\
\mathbf{O}_t &= \mathbf{H}t \mathbf{W}{hq} + \mathbf{b}_q
\end{aligned}\end{split}
$$

  • 将前向隐状态$\overrightarrow{\mathbf{H}}_t$和反向隐状态$\overleftarrow{\mathbf{H}}_t$连接起来， 获得需要送入输出层的隐状态$\mathbf{H}_t \in \mathbb{R}^{n \times 2h}$，在具有多个隐藏层的深度双向循环神经网络中， 该信息作为输入传递到下一个双向层。
  • 权重矩阵$\mathbf{W}_{hq} \in \mathbb{R}^{2h \times q}$和偏置$\mathbf{b}_q \in \mathbb{R}^{1 \times q}$是输出层的模型参数。 事实上，这两个方向可以拥有不同数量的隐藏单元。

模型的计算代价及其应用

  • 双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。 也就是说，我们使用来自过去和未来的观测信息来预测当前的观测。 但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的。 因为在预测下一个词元时，我们终究无法知道下一个词元的下文是什么， 所以将不会得到很好的精度。 具体地说，在训练期间，我们能够利用过去和未来的数据来估计现在空缺的词； 而在测试期间，我们只有过去的数据，因此精度将会很差。 下面的实验将说明这一点。
  • 另一个严重问题是，双向循环神经网络的计算速度非常慢。 其主要原因是网络的前向传播需要在双向层中进行前向和后向递归， 并且网络的反向传播还依赖于前向传播的结果。 因此，梯度求解将有一个非常长的链。
  • 双向层的使用在实践中非常少，并且仅仅应用于部分场合。 例如，填充缺失的单词、词元注释（例如，用于命名实体识别） 以及作为序列处理流水线中的一个步骤对序列进行编码（例如，用于机器翻译）。 在 14.8节和 15.2节中， 我们将介绍如何使用双向循环神经网络编码文本序列。

非常不适合做推理哈，主要用于做特征提取昂！

双向循环神经网络的错误应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import torch
from torch import nn
from d2l import torch as d2l

# 加载数据
batch_size, num_steps, device = 32, 35, d2l.try_gpu()
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 通过设置“bidirective=True”来定义双向LSTM模型
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers, bidirectional=True)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
# 训练模型
num_epochs, lr = 500, 1
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

import torch
from torch import nn
from d2l import torch as d2l

# 加载数据
batch_size, num_steps, device = 32, 35, d2l.try_gpu()
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 通过设置“bidirective=True”来定义双向LSTM模型
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers, bidirectional=True)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
# 训练模型
num_epochs, lr = 500, 1
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

# result，非常烂，不要用来做推理！！！
perplexity 1.1, 135912.3 tokens/sec on cuda:0
time travellerererererererererererererererererererererererererer
travellerererererererererererererererererererererererererer

Summary

  • 双向循环神经网络通过反向更新的隐藏层来利用方向时间信息
  • 通常用来对序列抽取特征、填空，而不是预测未来

机器翻译与数据集

  • 机器翻译正是将输入序列转换成输出序列的 序列转换模型（sequence transduction）的核心问题。 序列转换模型在各类现代人工智能应用中发挥着至关重要的作用。机器翻译（machine translation）指的是 将序列从一种语言自动翻译成另一种语言
  • Dependencies
1
2
3
import os
import torch
from d2l import torch as d2l

下载和预处理数据集

  • 由Tatoeba项目的双语句子对 组成的“英－法”数据集，数据集中的每一行都是制表符分隔的文本序列对， 序列对由英文文本序列和翻译后的法语文本序列组成。 请注意，每个文本序列可以是一个句子， 也可以是包含多个句子的一个段落。 在这个将英语翻译成法语的机器翻译问题中， 英语是源语言（source language）， 法语是目标语言（target language）。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#@save
d2l.DATA_HUB['fra-eng'] = (d2l.DATA_URL + 'fra-eng.zip',
                           '94646ad1522d915e7b0f9296181140edcf86a4f5')

#@save
def read_data_nmt():
    """载入“英语－法语”数据集"""
    data_dir = d2l.download_extract('fra-eng')
    with open(os.path.join(data_dir, 'fra.txt'), 'r',
             encoding='utf-8') as f:
        return f.read()

raw_text = read_data_nmt()
print(raw_text[:75])
  • 原始文本数据需要经过几个预处理步骤。 例如，我们用空格代替不间断空格（non-breaking space）， 使用小写字母替换大写字母，并在单词和标点符号之间插入空格。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#@save
def preprocess_nmt(text):
    """预处理“英语－法语”数据集"""
    def no_space(char, prev_char):
        return char in set(',.!?') and prev_char != ' '

    # 使用空格替换不间断空格
    # 使用小写字母替换大写字母
    text = text.replace('\u202f', ' ').replace('\xa0', ' ').lower()
    # 在单词和标点符号之间插入空格
    out = [' ' + char if i > 0 and no_space(char, text[i - 1]) else char
           for i, char in enumerate(text)]
    return ''.join(out)

text = preprocess_nmt(raw_text)
print(text[:80])

词元化

  • 与 8.3节中的字符级词元化不同， 在机器翻译中，我们更喜欢单词级词元化 （最先进的模型可能使用更高级的词元化技术）。 下面的tokenize_nmt函数对前num_examples个文本序列对进行词元， 其中每个词元要么是一个词，要么是一个标点符号。 此函数返回两个词元列表：source和target： source[i]是源语言（这里是英语）第i个文本序列的词元列表， target[i]是目标语言（这里是法语）第i个文本序列的词元列表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#@save
def tokenize_nmt(text, num_examples=None):
    """词元化“英语－法语”数据数据集"""
    source, target = [], []
    for i, line in enumerate(text.split('\n')):
        if num_examples and i > num_examples:
            break
        parts = line.split('\t')
        if len(parts) == 2:
            source.append(parts[0].split(' '))
            target.append(parts[1].split(' '))
    return source, target

source, target = tokenize_nmt(text)
source[:6], target[:6]
  • 绘制每个文本序列所包含的词元数量的直方图。 在这个简单的“英－法”数据集中，大多数文本序列的词元数量少于20个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#@save
def show_list_len_pair_hist(legend, xlabel, ylabel, xlist, ylist):
    """绘制列表长度对的直方图"""
    d2l.set_figsize()
    _, _, patches = d2l.plt.hist(
        [[len(l) for l in xlist], [len(l) for l in ylist]])
    d2l.plt.xlabel(xlabel)
    d2l.plt.ylabel(ylabel)
    for patch in patches[1].patches:
        patch.set_hatch('/')
    d2l.plt.legend(legend)

show_list_len_pair_hist(['source', 'target'], '# tokens per sequence',
                        'count', source, target);

词表

  • 我们可以分别为源语言和目标语言构建两个词表。 使用单词级词元化时，词表大小将明显大于使用字符级词元化时的词表大小。 为了缓解这一问题，这里我们将出现次数少于2次的低频率词元 视为相同的未知（“”）词元。 除此之外，我们还指定了额外的特定词元， 例如在小批量时用于将序列填充到相同长度的填充词元（“”）， 以及序列的开始词元（“”）和结束词元（“”）。 这些特殊词元在自然语言处理任务中比较常用。
1
2
3
src_vocab = d2l.Vocab(source, min_freq=2,
                      reserved_tokens=['<pad>', '<bos>', '<eos>'])
len(src_vocab)

加载数据集

  • 语言模型中的序列样本都有一个固定的长度， 这个固定长度是由 8.3节中的 num_steps（时间步数或词元数量）参数指定的。
  • 为了提高计算效率，我们仍然可以通过截断（truncation）和 填充（padding）方式实现一次只处理一个小批量的文本序列。 假设同一个小批量中的每个序列都应该具有相同的长度num_steps， 那么如果文本序列的词元数目少于num_steps时， 我们将继续在其末尾添加特定的“”词元， 直到其长度达到num_steps； 反之，我们将截断文本序列时，只取其前num_steps 个词元， 并且丢弃剩余的词元。这样，每个文本序列将具有相同的长度， 以便以相同形状的小批量进行加载。
1
2
3
4
5
6
7
8
#@save
def truncate_pad(line, num_steps, padding_token):
    """截断或填充文本序列"""
    if len(line) > num_steps:
        return line[:num_steps]  # 截断
    return line + [padding_token] * (num_steps - len(line))  # 填充

truncate_pad(src_vocab[source[0]], 10, src_vocab['<pad>'])
  • 可以将文本序列 转换成小批量数据集用于训练。 我们将特定的“”词元添加到所有序列的末尾， 用于表示序列的结束。 当模型通过一个词元接一个词元地生成序列进行预测时， 生成的“”词元说明完成了序列输出工作。 此外，我们还记录了每个文本序列的长度， 统计长度时排除了填充词元， 在稍后将要介绍的一些模型会需要这个长度信息。
1
2
3
4
5
6
7
8
9
#@save
def build_array_nmt(lines, vocab, num_steps):
    """将机器翻译的文本序列转换成小批量"""
    lines = [vocab[l] for l in lines]
    lines = [l + [vocab['<eos>']] for l in lines]
    array = torch.tensor([truncate_pad(
        l, num_steps, vocab['<pad>']) for l in lines])
    valid_len = (array != vocab['<pad>']).type(torch.int32).sum(1)
    return array, valid_len

训练模型

  • 我们定义load_data_nmt函数来返回数据迭代器， 以及源语言和目标语言的两种词表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#@save
def load_data_nmt(batch_size, num_steps, num_examples=600):
    """返回翻译数据集的迭代器和词表"""
    text = preprocess_nmt(read_data_nmt())
    source, target = tokenize_nmt(text, num_examples)
    src_vocab = d2l.Vocab(source, min_freq=2,
                          reserved_tokens=['<pad>', '<bos>', '<eos>'])
    tgt_vocab = d2l.Vocab(target, min_freq=2,
                          reserved_tokens=['<pad>', '<bos>', '<eos>'])
    src_array, src_valid_len = build_array_nmt(source, src_vocab, num_steps)
    tgt_array, tgt_valid_len = build_array_nmt(target, tgt_vocab, num_steps)
    data_arrays = (src_array, src_valid_len, tgt_array, tgt_valid_len)
    data_iter = d2l.load_array(data_arrays, batch_size)
    return data_iter, src_vocab, tgt_vocab
  • reading example
1
2
3
4
5
6
7
train_iter, src_vocab, tgt_vocab = load_data_nmt(batch_size=2, num_steps=8)
for X, X_valid_len, Y, Y_valid_len in train_iter:
    print('X:', X.type(torch.int32))
    print('X的有效长度:', X_valid_len)
    print('Y:', Y.type(torch.int32))
    print('Y的有效长度:', Y_valid_len)
    break

编码器-解码器架构

  • 机器翻译是序列转换模型的一个核心问题， 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出， 我们可以设计一个包含两个主要组件的架构： 第一个组件是一个编码器（encoder）： 它接受一个长度可变的序列作为输入， 并将其转换为具有固定形状的编码状态。 第二个组件是解码器（decoder）： 它将固定形状的编码状态映射到长度可变的序列。 这被称为编码器-解码器（encoder-decoder）架构，

../_images/encoder-decoder.svg

  • 编码器：输入编码成中间状态
  • 解码器：将中间状态解码成输出

CNN本质上也是一个编码-解码器呀，从图片中把图像特征“编码”，然后把中间特征“解码”成类别。

编码器

  • 编码器接口中，我们只指定长度可变的序列作为编码器的输入X。 任何继承这个Encoder基类的模型将完成代码实现。
1
2
3
4
5
6
7
8
9
10
11
from torch import nn


#@save
class Encoder(nn.Module):
    """编码器-解码器架构的基本编码器接口"""
    def __init__(self, **kwargs):
        super(Encoder, self).__init__(**kwargs)

    def forward(self, X, *args):
        raise NotImplementedError

解码器

  • 我们新增一个init_state函数， 用于将编码器的输出（enc_outputs）转换为编码后的状态。 注意，此步骤可能需要额外的输入，例如：输入序列的有效长度， 这在 9.5.4节中进行了解释。 为了逐个地生成长度可变的词元序列， 解码器在每个时间步都会将输入 （例如：在前一时间步生成的词元）和编码后的状态映射成当前时间步的输出词元。
1
2
3
4
5
6
7
8
9
10
11
#@save
class Decoder(nn.Module):
    """编码器-解码器架构的基本解码器接口"""
    def __init__(self, **kwargs):
        super(Decoder, self).__init__(**kwargs)

    def init_state(self, enc_outputs, *args):
        raise NotImplementedError

    def forward(self, X, state):
        raise NotImplementedError

合并编码器和解码器

  • “编码器-解码器”架构包含了一个编码器和一个解码器， 并且还拥有可选的额外的参数。 在前向传播中，编码器的输出用于生成编码状态， 这个状态又被解码器作为其输入的一部分。
1
2
3
4
5
6
7
8
9
10
11
12
#@save
class EncoderDecoder(nn.Module):
    """编码器-解码器架构的基类"""
    def __init__(self, encoder, decoder, **kwargs):
        super(EncoderDecoder, self).__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, enc_X, dec_X, *args):
        enc_outputs = self.encoder(enc_X, *args)
        dec_state = self.decoder.init_state(enc_outputs, *args)
        return self.decoder(dec_X, dec_state)

序列到序列学习（seq2seq）

网络结构

  • 循环神经网络编码器使用长度可变的序列作为输入， 将其转换为固定形状的隐状态。 换言之，输入序列的信息被编码到循环神经网络编码器的隐状态中。 为了连续生成输出序列的词元， 独立的循环神经网络解码器是基于输入序列的编码信息 和输出序列已经看见的或者生成的词元来预测下一个词元。

../_images/seq2seq.svg

  • 编码器是一个RNN,读取输入句子。可以是双向。
  • 解码器使用另外一个RNN来输出。

../_images/seq2seq-details.svg

  • 编码器是没有输出的RNN。
  • 编码器最后时间步的隐状态，用作解码器的初识隐状态。
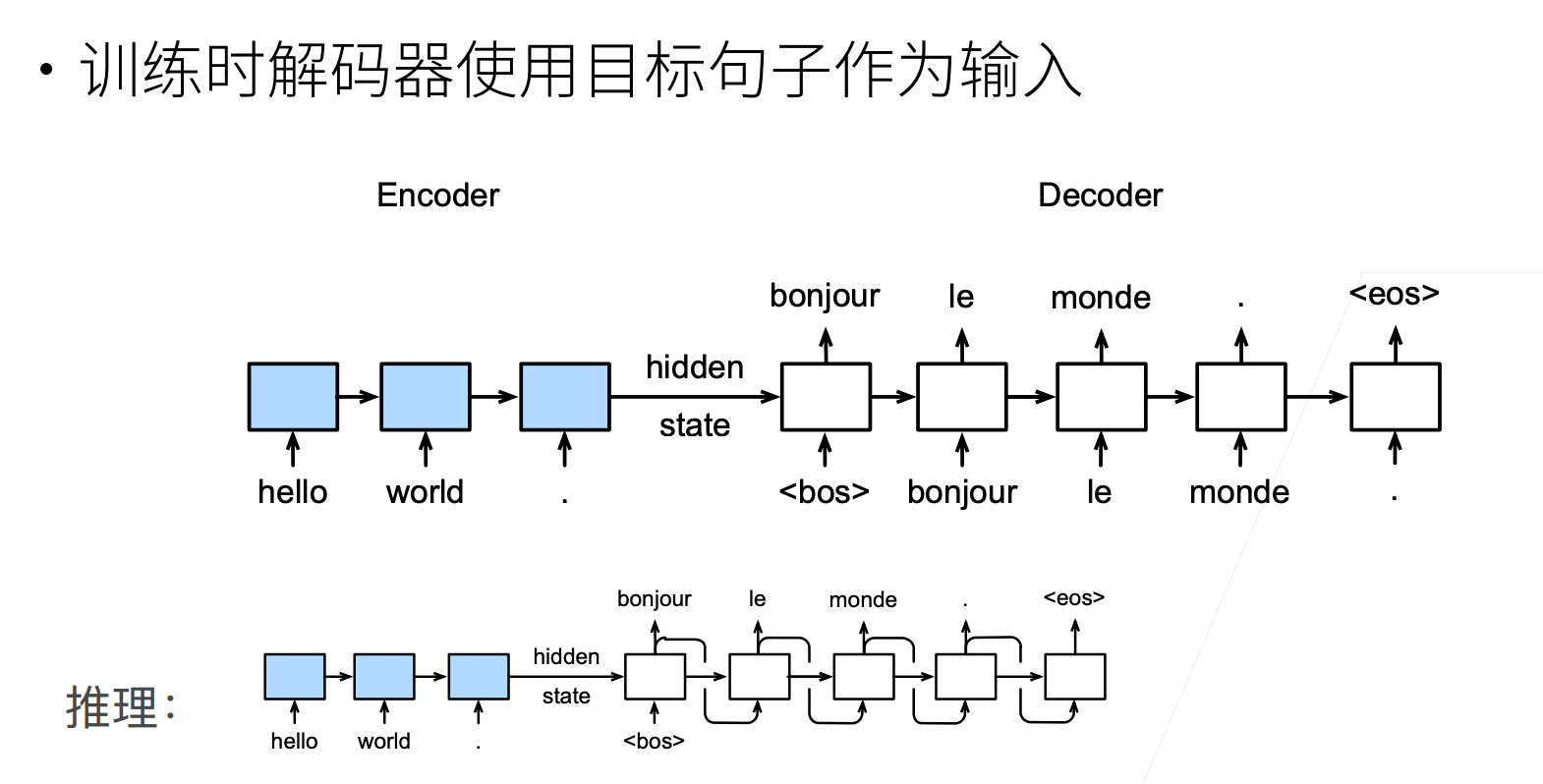
  • 训练和推理有所不同：训练和推理的时候，Encoder输入都是一样的。Decoder训练和推理的时候不一样。训练的时候，用的就是真正的目标句子作为输入。推理的时候，用上一时刻的预测结果，作为下一时刻的输入。

image-20230815170437213

预测序列的评估

  • 我们可以通过与真实的标签序列进行比较来评估预测序列。 虽然 (Papineni et al., 2002) 提出的BLEU（bilingual evaluation understudy） 最先是用于评估机器翻译的结果， 但现在它已经被广泛用于测量许多应用的输出序列的质量。 原则上说，对于预测序列中的任意n元语法（n-grams）， BLEU的评估都是这个n元语法是否出现在标签序列中。
    • $p_n$是预测中所有n-gram的精度，标签序列A B C D E F和预测序列A B B C D，有：$p_1$=4/5, $p_2$= 3/4, $p_3$= 1/3, $p_4$=0
    • 我们将BLEU定义为：

$$
\exp\left(\min\left(0, 1 - \frac{\mathrm{len}{\text{label}}}{\mathrm{len}{\text{pred}}}\right)\right) \prod_{n=1}^k p_n^{1/2^n},
$$

惩罚过短的预测，长匹配有高权重

代码实现

编码器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#@save
class Seq2SeqEncoder(d2l.Encoder):
    """用于序列到序列学习的循环神经网络编码器"""
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqEncoder, self).__init__(**kwargs)
        # 嵌入层
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size, num_hiddens, num_layers,
                          dropout=dropout)

    def forward(self, X, *args):
        # 输出'X'的形状：(batch_size,num_steps,embed_size)
        X = self.embedding(X)
        # 在循环神经网络模型中，第一个轴对应于时间步
        X = X.permute(1, 0, 2)
        # 如果未提及状态，则默认为0
        output, state = self.rnn(X)
        # output的形状:(num_steps,batch_size,num_hiddens)
        # state的形状:(num_layers,batch_size,num_hiddens)
        return output, state

注意GRU这种nn.GRU是没有输出层的，没有和之前一样用一个Dense作为输出层的原因是，编码器不需要输出。

  • usage
1
2
3
4
5
6
encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16,
                         num_layers=2)
encoder.eval()
X = torch.zeros((4, 7), dtype=torch.long)
output, state = encoder(X)
output.shape, state.shape

解码器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Seq2SeqDecoder(d2l.Decoder):
    """用于序列到序列学习的循环神经网络解码器"""
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqDecoder, self).__init__(**kwargs)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,
                          dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, *args):
        return enc_outputs[1]

    def forward(self, X, state):
        # 输出'X'的形状：(batch_size,num_steps,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        # 广播context，使其具有与X相同的num_steps
        context = state[-1].repeat(X.shape[0], 1, 1)
        X_and_context = torch.cat((X, context), 2)
        output, state = self.rnn(X_and_context, state)
        output = self.dense(output).permute(1, 0, 2)
        # output的形状:(batch_size,num_steps,vocab_size)
        # state的形状:(num_layers,batch_size,num_hiddens)
        return output, state

Decoder有输出层哈！！！

init_state中的enc_outputs就是上面编码器的输出，enc_outputs[1]就是state

  • usage
1
2
3
4
5
6
decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8, num_hiddens=16,
                         num_layers=2)
decoder.eval()
state = decoder.init_state(encoder(X))
output, state = decoder(X, state)
output.shape, state.shape

损失函数

  • 在每个时间步，解码器预测了输出词元的概率分布。 类似于语言模型，可以使用softmax来获得分布， 并通过计算交叉熵损失函数来进行优化。 回想一下 9.5节中， 特定的填充词元被添加到序列的末尾， 因此不同长度的序列可以以相同形状的小批量加载。 但是，我们应该将填充词元的预测排除在损失函数的计算之外。
  • 我们可以使用下面的sequence_mask函数 通过零值化屏蔽不相关的项， 以便后面任何不相关预测的计算都是与零的乘积，结果都等于零。 例如，如果两个序列的有效长度（不包括填充词元）分别为1和2， 则第一个序列的第一项和第二个序列的前两项之后的剩余项将被清除为零。
1
2
3
4
5
6
7
8
9
10
11
#@save
def sequence_mask(X, valid_len, value=0):
    """在序列中屏蔽不相关的项"""
    maxlen = X.size(1)
    mask = torch.arange((maxlen), dtype=torch.float32,
                        device=X.device)[None, :] < valid_len[:, None]
    X[~mask] = value
    return X

X = torch.tensor([[1, 2, 3], [4, 5, 6]])
sequence_mask(X, torch.tensor([1, 2]))

把valid_len以外的清成0，把填充的东西标出来。

填充的东西不算数，不参与softmax的计算昂！！！

  • 我们还可以使用此函数屏蔽最后几个轴上的所有项。如果愿意，也可以使用指定的非零值来替换这些项。
1
2
X = torch.ones(2, 3, 4)
sequence_mask(X, torch.tensor([1, 2]), value=-1)
  • 我们可以通过扩展softmax交叉熵损失函数来遮蔽不相关的预测。 最初，所有预测词元的掩码都设置为1。 一旦给定了有效长度，与填充词元对应的掩码将被设置为0。 最后，将所有词元的损失乘以掩码，以过滤掉损失中填充词元产生的不相关预测。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#@save
class MaskedSoftmaxCELoss(nn.CrossEntropyLoss):
    """带遮蔽的softmax交叉熵损失函数"""
    # pred的形状：(batch_size,num_steps,vocab_size)
    # label的形状：(batch_size,num_steps)
    # valid_len的形状：(batch_size,)
    def forward(self, pred, label, valid_len):
        weights = torch.ones_like(label)
        weights = sequence_mask(weights, valid_len)
        self.reduction='none'
        unweighted_loss = super(MaskedSoftmaxCELoss, self).forward(
            pred.permute(0, 2, 1), label)
        weighted_loss = (unweighted_loss * weights).mean(dim=1)
        return weighted_loss

对每个句子的loss求一下平均，对每个样本返回一个loss

训练

  • 在下面的循环训练过程中，如 图9.7.1所示， 特定的序列开始词元（“”）和 原始的输出序列（不包括序列结束词元“”） 拼接在一起作为解码器的输入。 这被称为强制教学（teacher forcing）， 因为原始的输出序列（词元的标签）被送入解码器。 或者，将来自上一个时间步的预测得到的词元作为解码器的当前输入。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#@save
def train_seq2seq(net, data_iter, lr, num_epochs, tgt_vocab, device):
    """训练序列到序列模型"""
    def xavier_init_weights(m):
        if type(m) == nn.Linear:
            nn.init.xavier_uniform_(m.weight)
        if type(m) == nn.GRU:
            for param in m._flat_weights_names:
                if "weight" in param:
                    nn.init.xavier_uniform_(m._parameters[param])

    net.apply(xavier_init_weights)
    net.to(device)
    optimizer = torch.optim.Adam(net.parameters(), lr=lr)
    loss = MaskedSoftmaxCELoss()
    net.train()
    animator = d2l.Animator(xlabel='epoch', ylabel='loss',
                     xlim=[10, num_epochs])
    for epoch in range(num_epochs):
        timer = d2l.Timer()
        metric = d2l.Accumulator(2)  # 训练损失总和，词元数量
        for batch in data_iter:
            optimizer.zero_grad()
            X, X_valid_len, Y, Y_valid_len = [x.to(device) for x in batch]
            bos = torch.tensor([tgt_vocab['<bos>']] * Y.shape[0],
                          device=device).reshape(-1, 1)
            dec_input = torch.cat([bos, Y[:, :-1]], 1)  # 强制教学
            Y_hat, _ = net(X, dec_input, X_valid_len)
            l = loss(Y_hat, Y, Y_valid_len)
            l.sum().backward()      # 损失函数的标量进行“反向传播”
            d2l.grad_clipping(net, 1)
            num_tokens = Y_valid_len.sum()
            optimizer.step()
            with torch.no_grad():
                metric.add(l.sum(), num_tokens)
        if (epoch + 1) % 10 == 0:
            animator.add(epoch + 1, (metric[0] / metric[1],))
    print(f'loss {metric[0] / metric[1]:.3f}, {metric[1] / timer.stop():.1f} '
        f'tokens/sec on {str(device)}')
  • 现在，在机器翻译数据集上，我们可以 创建和训练一个循环神经网络“编码器－解码器”模型用于序列到序列的学习。
1
2
3
4
5
6
7
8
9
10
11
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 300, d2l.try_gpu()

train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = Seq2SeqEncoder(len(src_vocab), embed_size, num_hiddens, num_layers,
                        dropout)
decoder = Seq2SeqDecoder(len(tgt_vocab), embed_size, num_hiddens, num_layers,
                        dropout)
net = d2l.EncoderDecoder(encoder, decoder)
train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)

预测

  • 为了采用一个接着一个词元的方式预测输出序列， 每个解码器当前时间步的输入都将来自于前一时间步的预测词元。 与训练类似，序列开始词元（“”） 在初始时间步被输入到解码器中。 当输出序列的预测遇到序列结束词元（“”）时，预测就结束了。

../_images/seq2seq-predict.svg

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#@save
def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps,
                    device, save_attention_weights=False):
    """序列到序列模型的预测"""
    # 在预测时将net设置为评估模式
    net.eval()
    src_tokens = src_vocab[src_sentence.lower().split(' ')] + [
        src_vocab['<eos>']]
    enc_valid_len = torch.tensor([len(src_tokens)], device=device)
    src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
    # 添加批量轴
    enc_X = torch.unsqueeze(
        torch.tensor(src_tokens, dtype=torch.long, device=device), dim=0)
    enc_outputs = net.encoder(enc_X, enc_valid_len)
    dec_state = net.decoder.init_state(enc_outputs, enc_valid_len)
    # 添加批量轴
    dec_X = torch.unsqueeze(torch.tensor(
        [tgt_vocab['<bos>']], dtype=torch.long, device=device), dim=0)
    output_seq, attention_weight_seq = [], []
    for _ in range(num_steps):
        Y, dec_state = net.decoder(dec_X, dec_state)
        # 我们使用具有预测最高可能性的词元，作为解码器在下一时间步的输入
        dec_X = Y.argmax(dim=2)
        pred = dec_X.squeeze(dim=0).type(torch.int32).item()
        # 保存注意力权重（稍后讨论）
        if save_attention_weights:
            attention_weight_seq.append(net.decoder.attention_weights)
        # 一旦序列结束词元被预测，输出序列的生成就完成了
        if pred == tgt_vocab['<eos>']:
            break
        output_seq.append(pred)
    return ' '.join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq

预测序列的评估

  • bleu的实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def bleu(pred_seq, label_seq, k):  #@save
    """计算BLEU"""
    pred_tokens, label_tokens = pred_seq.split(' '), label_seq.split(' ')
    len_pred, len_label = len(pred_tokens), len(label_tokens)
    score = math.exp(min(0, 1 - len_label / len_pred))
    for n in range(1, k + 1):
        num_matches, label_subs = 0, collections.defaultdict(int)
        for i in range(len_label - n + 1):
            label_subs[' '.join(label_tokens[i: i + n])] += 1
        for i in range(len_pred - n + 1):
            if label_subs[' '.join(pred_tokens[i: i + n])] > 0:
                num_matches += 1
                label_subs[' '.join(pred_tokens[i: i + n])] -= 1
        score *= math.pow(num_matches / (len_pred - n + 1), math.pow(0.5, n))
    return score
  • 利用训练好的循环神经网络“编码器－解码器”模型， 将几个英语句子翻译成法语，并计算BLEU的最终结果。
1
2
3
4
5
6
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
    translation, attention_weight_seq = predict_seq2seq(
        net, eng, src_vocab, tgt_vocab, num_steps, device)
    print(f'{eng} => {translation}, bleu {bleu(translation, fra, k=2):.3f}')

束搜索（Beam Search）

  • 本节将首先介绍贪心搜索（greedy search）策略， 并探讨其存在的问题，然后对比其他替代策略： 穷举搜索（exhaustive search）和束搜索（beam search）。
  • 贪心搜索、束搜索、穷举搜索，分别是找1个输出，多个输出、所有输出。

贪心搜索

  • seq2seq就是贪心搜索，我们都将基于贪心搜索从$\mathcal{Y}$中找到具有最高条件概率的词元，即：

$$
y_{t’} = \operatorname*{argmax}{y \in \mathcal{Y}} P(y \mid y_1, \ldots, y{t’-1}, \mathbf{c})
$$

一旦输出序列包含了“”或者达到其最大长度$T’$，则输出完成。

../_images/s2s-prob1.svg

在每个时间步，贪心搜索选择具有最高条件概率的词元。$0.5\times0.4\times0.4\times0.6 = 0.048$

../_images/s2s-prob2.svg

在时间步2，选择具有第二高条件概率的词元“C”（而非最高条件概率的词元）。$0.5\times0.3 \times0.6\times0.6=0.054$

  • 可以看到，贪心不是最优的！！！贪心很可能不是最优的！

穷举搜索

  • 如果目标是获得最优序列， 我们可以考虑使用穷举搜索（exhaustive search）： 穷举地列举所有可能的输出序列及其条件概率， 然后计算输出条件概率最高的一个。
  • 虽然我们可以使用穷举搜索来获得最优序列， 但其计算量$\mathcal{O}(\left|\mathcal{Y}\right|^{T’})$可能高的惊人。 例如，当$|\mathcal{Y}|=10000$和$T’=10$时， 我们需要评估$10000^{10} = 10^{40}$序列， 这是一个极大的数，现有的计算机几乎不可能计算它。 然而，贪心搜索的计算量$\mathcal{O}(\left|\mathcal{Y}\right|T’)$通它要显著地小于穷举搜索。 例如，当$|\mathcal{Y}|=10000$和$T’=10$时， 我们只需要评估$10000\times10=10^5$个序列。

束搜索

  • 如果精度最重要，则显然是穷举搜索。 如果计算成本最重要，则显然是贪心搜索。 而束搜索的实际应用则介于这两个极端之间。
  • 束搜索（beam search）是贪心搜索的一个改进版本。 它有一个超参数，名为束宽（beam size）k。 在时间步1，我们选择具有最高条件概率的k个词元。 这k个词元将分别是k个候选输出序列的第一个词元。 在随后的每个时间步，基于上一时间步的k个候选输出序列， 我们将继续从$k\left|\mathcal{Y}\right|$个可能的选择中 挑出具有最高条件概率的k个候选输出序列。

../_images/beam-search.svg

  • 我们会得到六个候选输出序列：A, C, AB, CE, ABD, CED。最后，基于这六个序列（例如，丢弃包括“”和之后的部分）， 我们获得最终候选输出序列集合。 然后我们选择其中条件概率乘积最高的序列作为输出序列

$$
\frac{1}{L^\alpha} \log P(y_1, \ldots, y_{L}\mid \mathbf{c}) = \frac{1}{L^\alpha} \sum_{t’=1}^L \log P(y_{t’} \mid y_1, \ldots, y_{t’-1}, \mathbf{c}),
$$

其中$L$是最终候选序列的长度， $\alpha$通常设置为0.75。 因为一个较长的序列在 (9.8.4) 的求和中会有更多的对数项， 因此分母中的$L^\alpha$用于惩罚长序列。

  • 束搜索的计算量为$\mathcal{O}(k\left|\mathcal{Y}\right|T’)$， 这个结果介于贪心搜索和穷举搜索之间。 实际上，贪心搜索可以看作一种束宽为1的特殊类型的束搜索。 通过灵活地选择束宽，束搜索可以在正确率和计算代价之间进行权衡。
  • Beam Search就是在每次搜索的时候，保留k个最好的候选，然后最后进行挑选。k = 1就是贪心，k = n就是穷举。

References

  1. GRU Q&A
  2. LSTM Q&A
  3. 深度RNN Q&A
  4. 双向循环RNN Q&A
  5. Seq2Seq Q&A
AI
#研0自学
D2L-10-Modern Recurrent Neural Networks
https://alexanderliu-creator.github.io/2023/08/14/d2l-10-modern-recurrent-neural-networks/
作者
Alexander Liu
发布于
2023年8月14日
许可协议