Recommendation System
本文最后更新于:2 个月前
学点新东西,拖了很久的Recommended System,启动!
Shuseng Wang的公开课
Basic Recommendation System Knowledge
Conversion process, indicators and experiment process
用户在小红书中,推荐算法帮助用户进行的转化流程
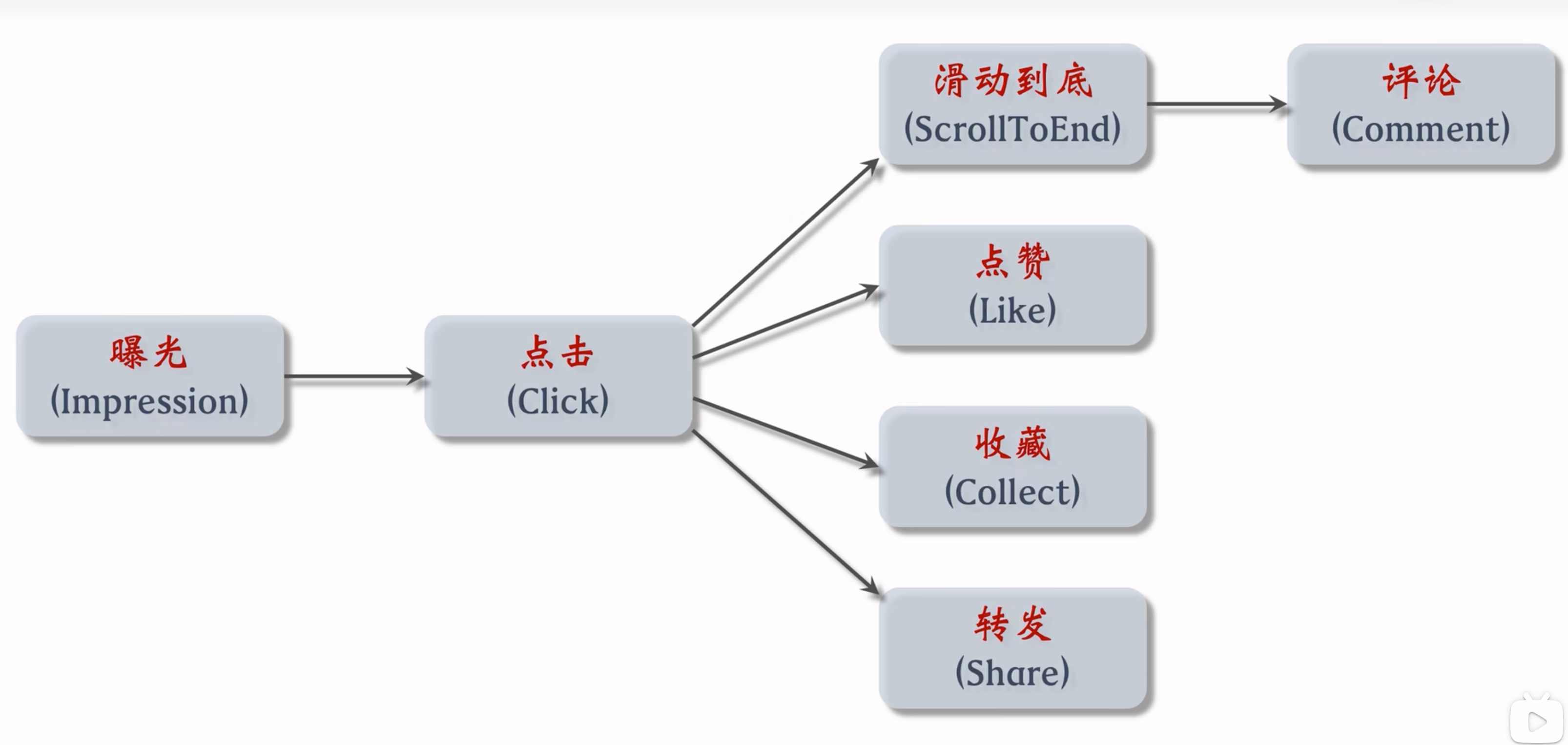
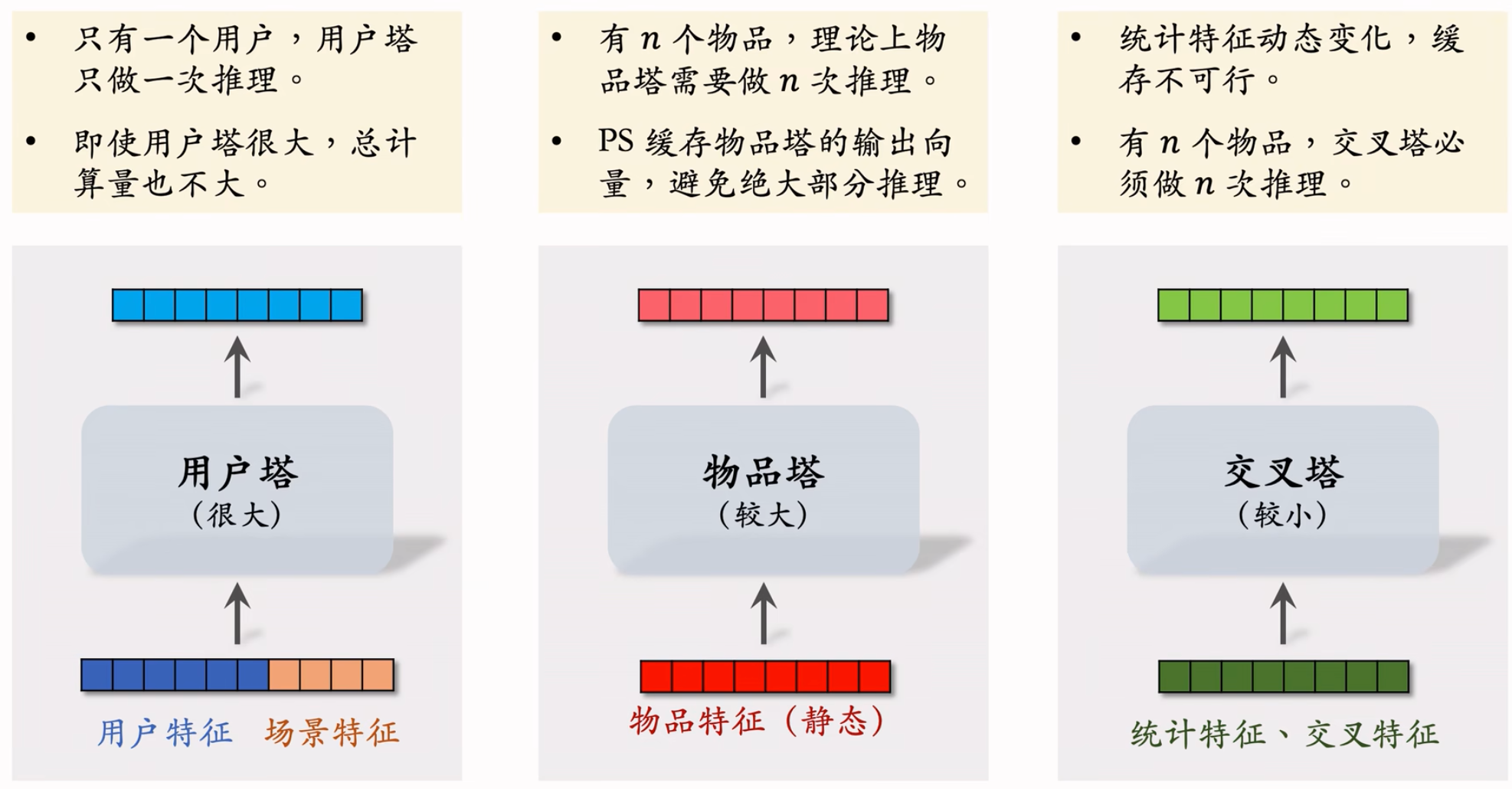
- 不同系统不一样,淘宝/Youtube前两步都是Impression等,但是抖音就不一样。
重要指标:
短期消费指标
- 点击率 = 点击次数/曝光次数
- 点赞率 = 点赞次数/点击次数
- 收藏率 = 收藏次数/点击次数
- 转发率 = 转发次数/点击次数
- 阅读完成率 = 滑动到底次数/点击次数×f(笔记长度)
长期消费指标
- 多样性等 -> 用户粘性
最重要的指标—北极星指标
- 用户规模:日活用户数(DAU)、月活用户数(MAU)。
- 消费:人均使用推荐的时长、人均阅读笔记的数量。
- 发布:发布渗透率、人均发布量。
北极星指标比其他指标更重要!当发生冲突时,以北极星指标为准。北极星指标 都是线上指标,只能上线了才能获得。
实验流程:
- 离线实验:收集历史数据,在历史数据上做训练、测试。算法没有部署到产品中,没有跟用户交互。
- 小流量AB测试:把算法部署到实际产品中,用户实际跟算法做交互。
- 全流量上线:小流量AB后,效果好,逐渐放量推全。
Recommendation system workflow
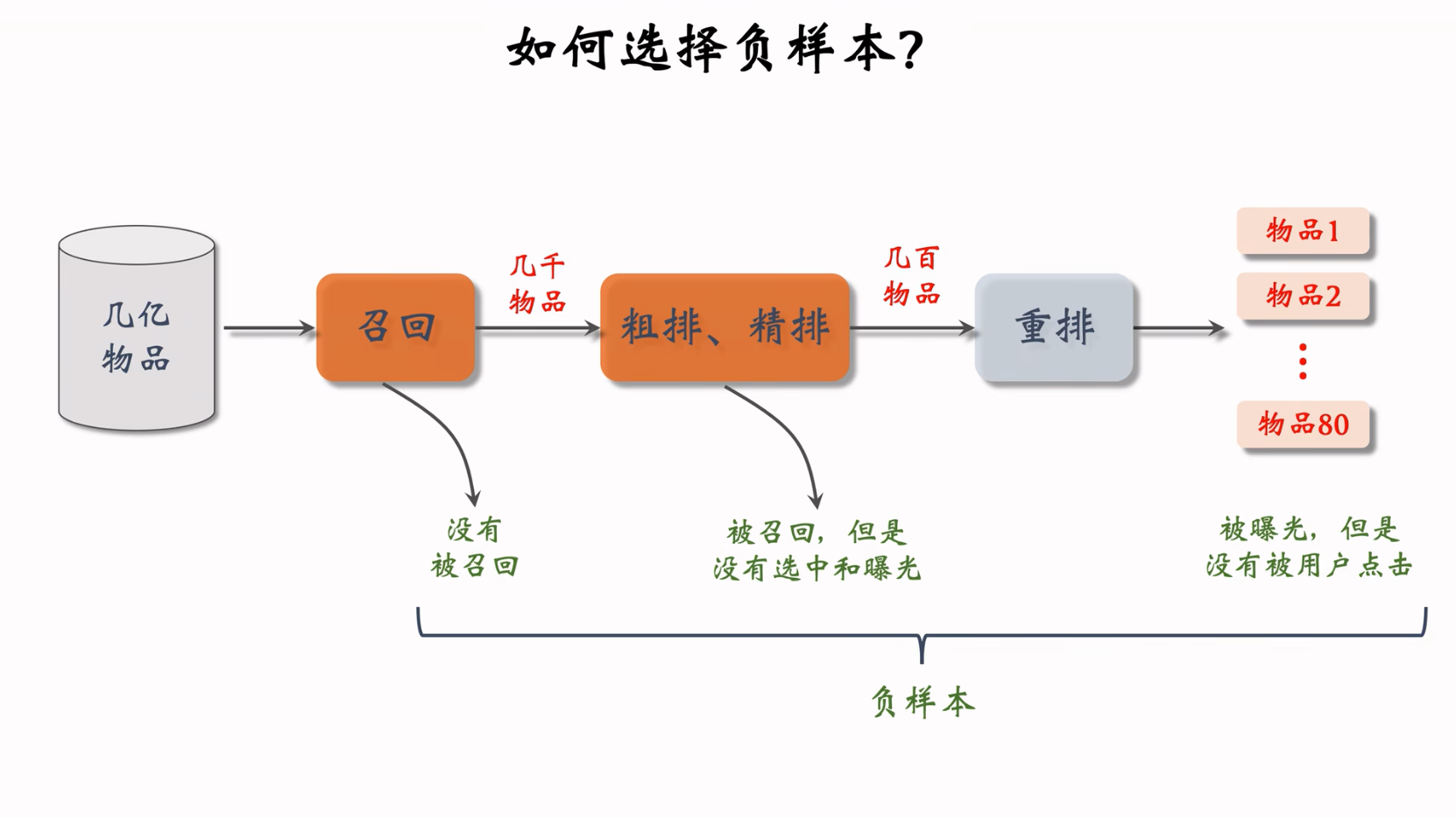
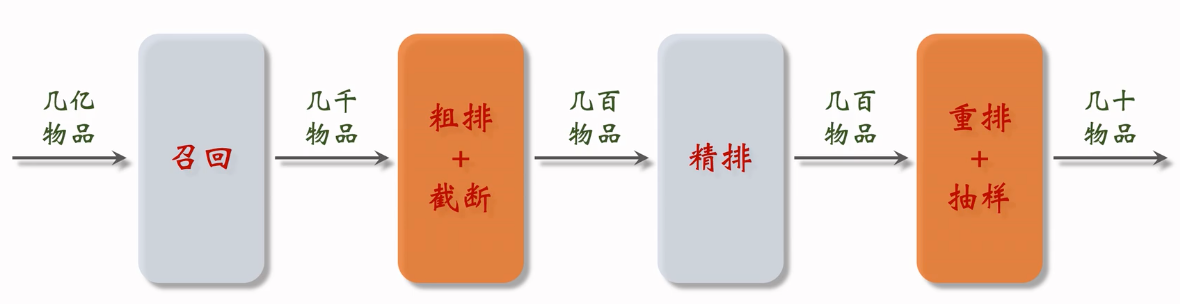
链路概览:
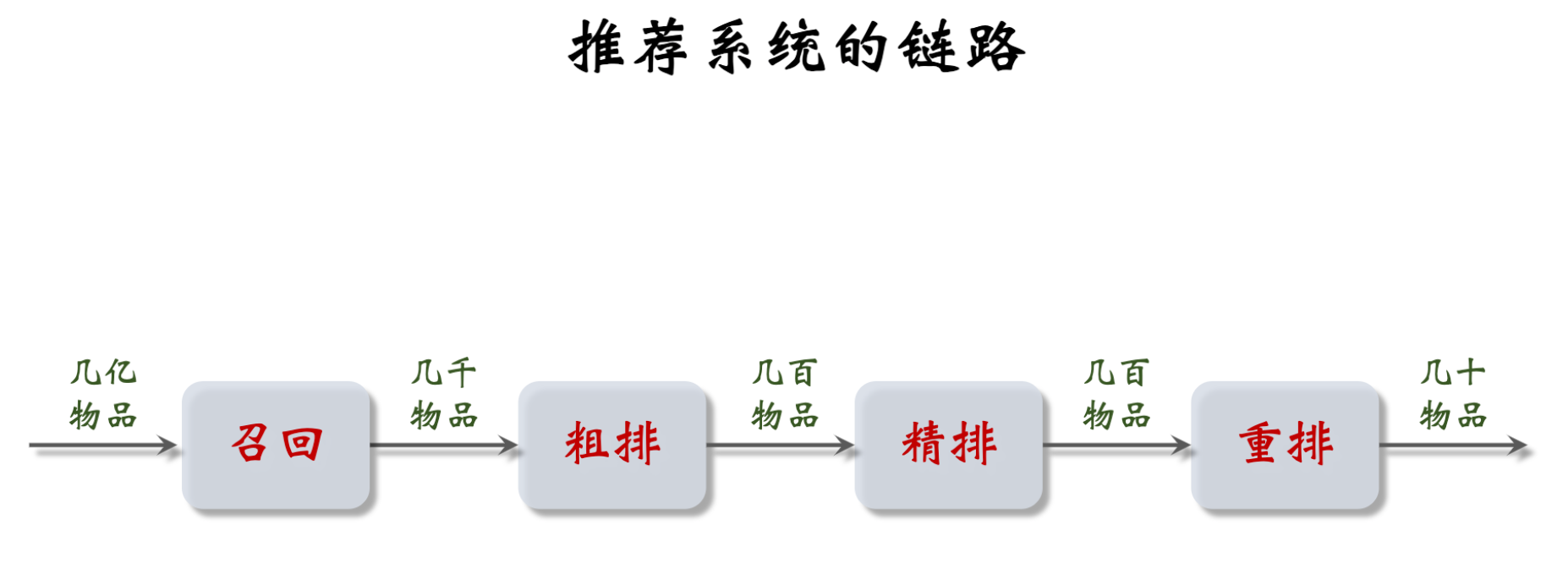
- 召回:从数据库中,通过多条召回通道进行召回,每条召回通道取回几十到几百篇笔记,总共召回几千篇笔记。
- 粗排:用规模比较小的机器学习模型给几千篇笔记逐一打分,按照分数和排序做截断,保留分数最高的几百篇笔记。
- 精排:用大规模的深度神经网络给几百篇笔记逐一打分,分数反映出用户对笔记的兴趣。可以截断,也可以不截断(小红书就是不做截断)。带着精排的分数,进入重排。
- 重排:根据精排分数和多样性分数做随机抽样,得到几十篇内容。然后把相似内容打散,插入广告和运营内容。
召回:
召回通道:协同过滤、双塔模型、关注的作者、等等
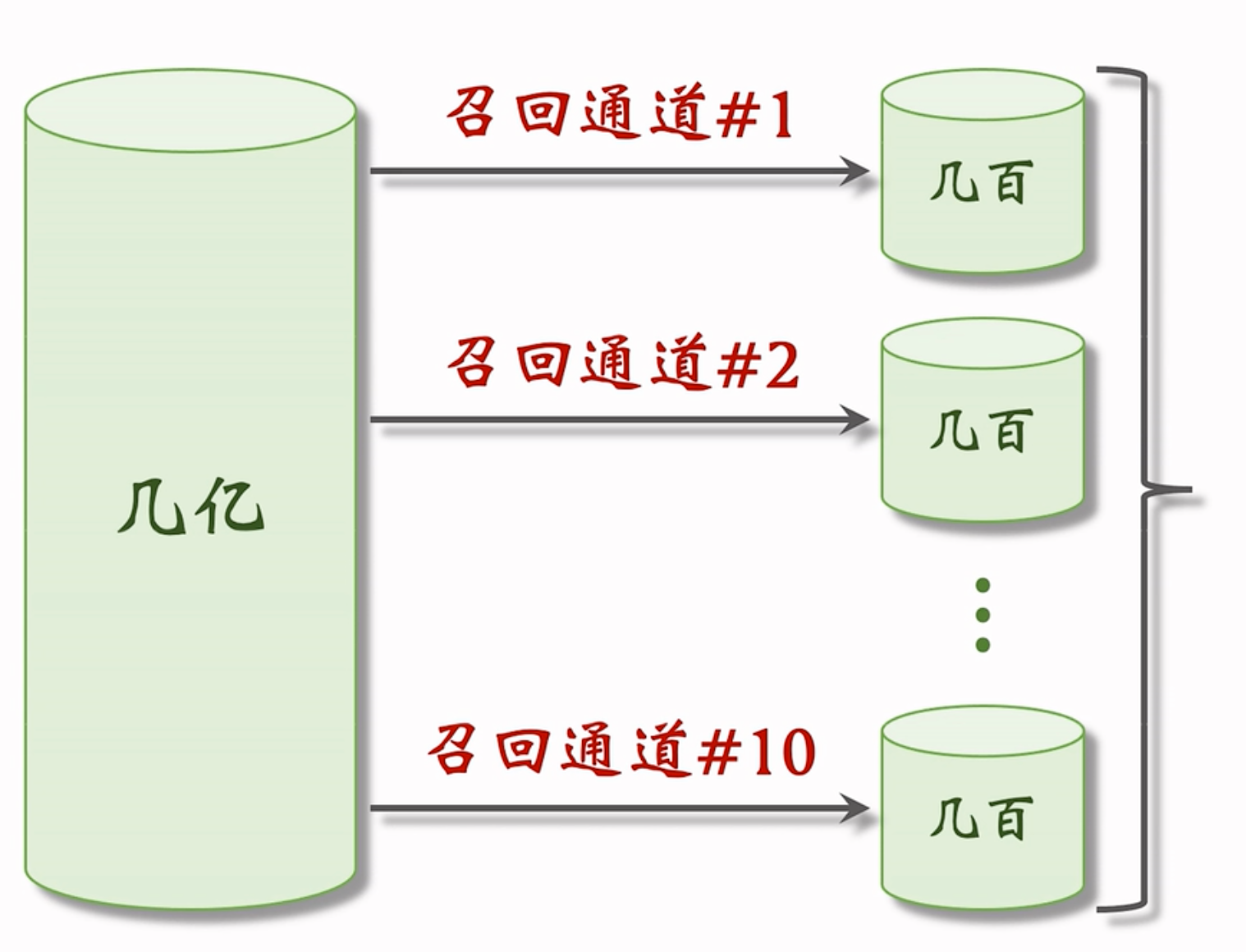
小红书有几十个召回通道,每个通道返回几十上百篇笔记。将所有召回通道的内容融合后,会去重,并过滤(例如去掉用户不喜欢的作者的笔记,不喜欢的话题)
粗排/精排:
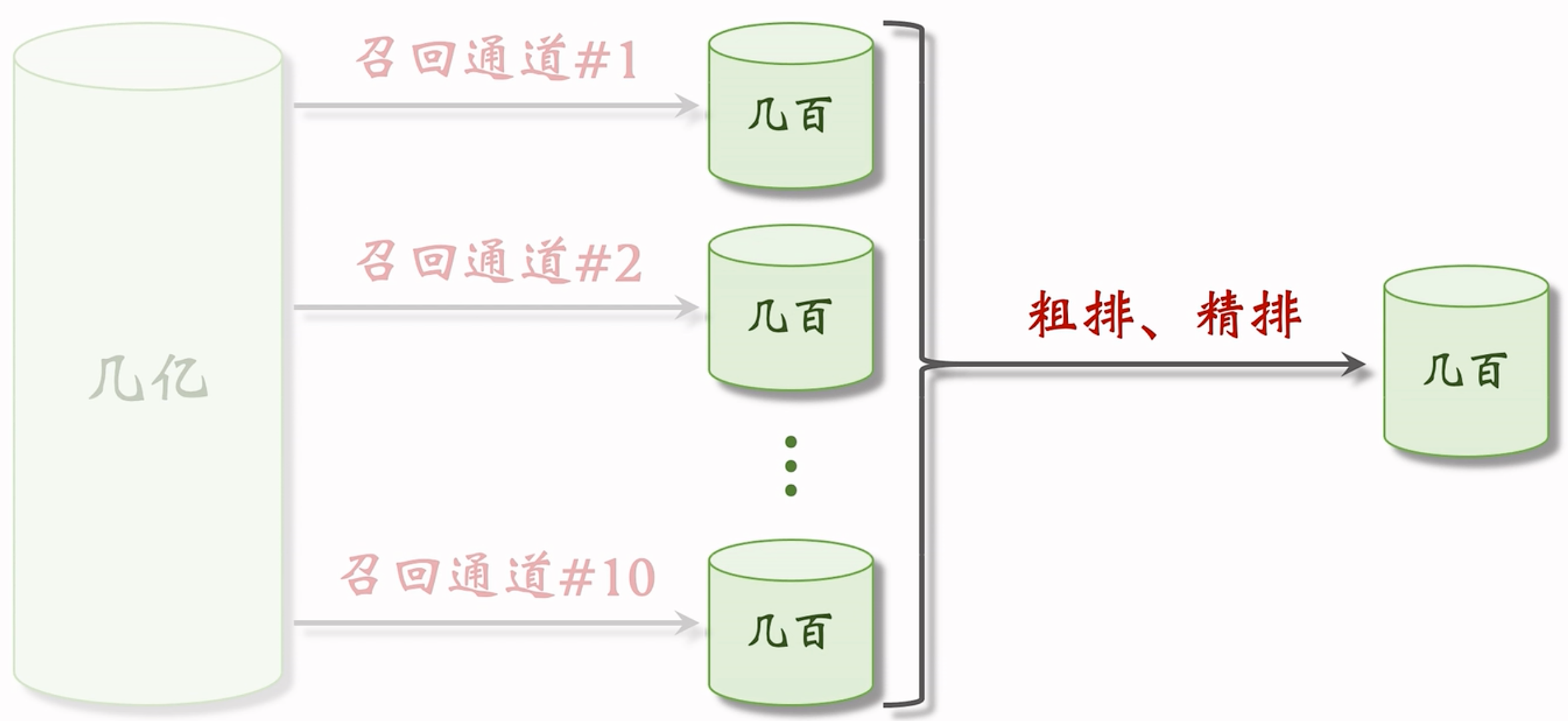
[几千] → 粗排 → [几百] → 精排 → [几百]
粗排模型小,速度快;精排用的模型大,计算量大,打分更可靠。
用粗排做筛选,再用精排 — 平衡计算量和准确性。
每篇笔记都有一个分数,表示用户对于笔记的兴趣有多高。(可以用于排序)
排序本质上就是输入一批特征,得到一批结果,融合得到一个最终的打分:
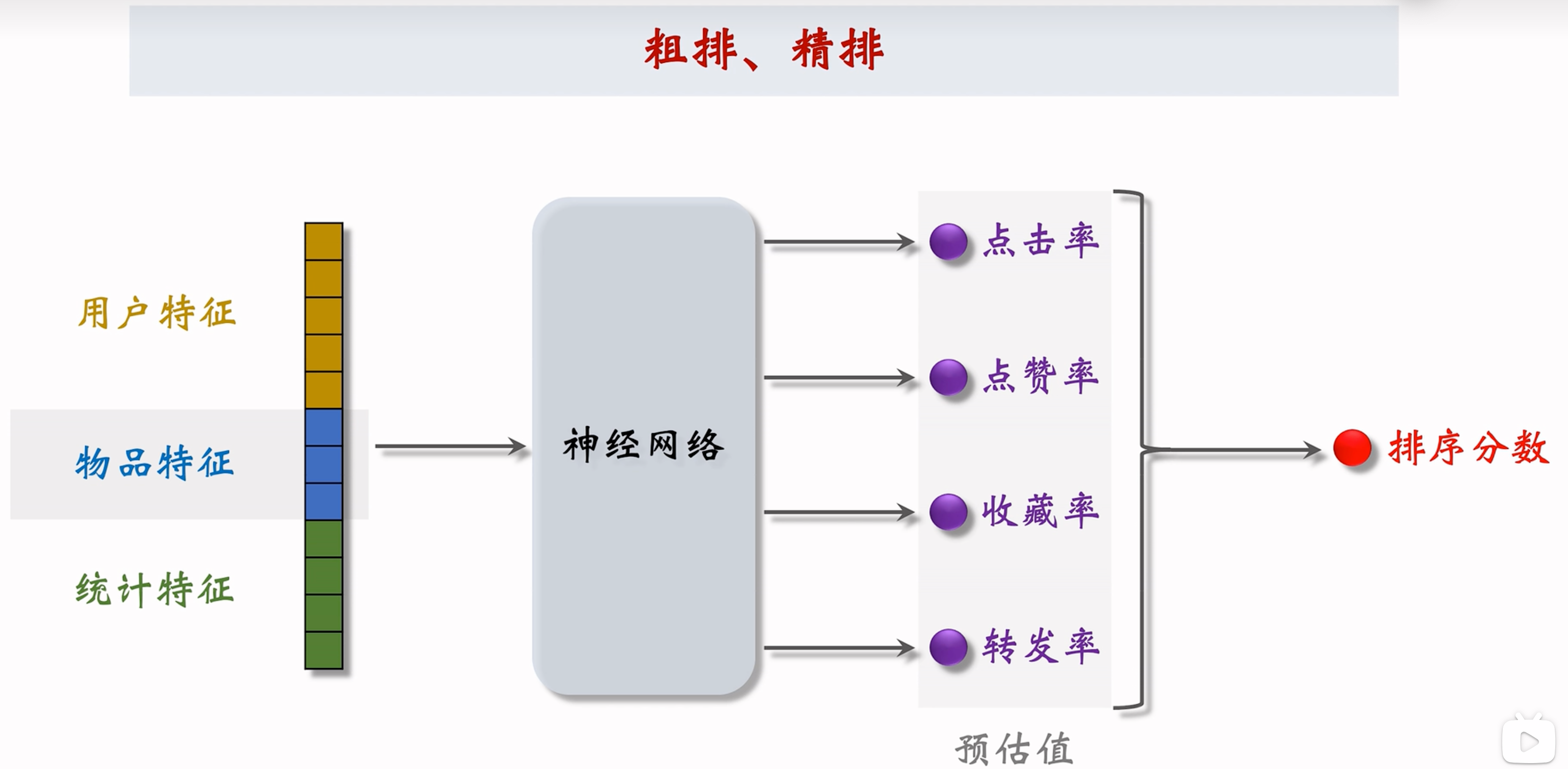
这一步骤的结果其实已经可以较好展示给用户了,但是此时结果还是不足,还有一些调整。
重排(主要是考虑多样性):做多样性抽样(比如 MMR、DPP),从几百篇中选出几十篇,抽样依据:精排分数、多样性。
用规则打散相似笔记,不能把内容过于相似的笔记,排在相邻的位置上。减少一个页面中的同质化内容:插入广告、运营推广内容,根据生态要求调整排序(例如:不能同时出很多美女图片)
总结
- 召回:用多条通道,取回几千篇笔记
- 粗排:用小规模神经网络,给几千篇笔记打分,选出分数最高的几百篇
- 精排:用大规模神经网络,给几百篇笔记打分
- 重排:做多样性抽样、规则打散、插入广告和运营笔记
召回和粗排是个大漏斗,这俩过滤掉的页面是最多的,从所有数据 -> 几千 -> 几百,这直接是对数量级的降维打击。
A/B Test
A/B 测试举例
- 召回团队实现了一种 GNN 召回通道,离线实验结果正向。(离线不等于上线哈)
- 线上的小流量 A/B 测试,不影响大多数用户的体验,考察新的召回通道对线上指标的影响。
- 模型中有一些参数,比如 GNN 的深度取值,需要用 A/B 测试选取最优参数。(可以同时开多组实验,查看不同参数的效果)
随机分桶(把用户分成小份儿,方便A/B test)
用户数量足够大的情况下,各个桶中用户的表现数据都是一样的哈(在所有的桶的环境都一样的条件下。)。
Case:
分b=10个桶,每个桶中有10%的用户。
首先用哈希函数把用户D映射成某个区间内的整数,然后把这些整数均匀随机分成b个桶。
改变部分桶的策略,进行实验对照:

计算每个桶的业务指标,比如DAU、人均使用推荐的时长、点击率、等等。
如果某个实验组指标显著优于对照组,则说明对应的策略有效,值得推全。
分层实验
- 流量不够用怎么办?
- 信息流产品的公司有很多部门和团队,大家都需要做A/B测试。推荐系统(召回、粗排、精排、重排),用户界面,广告等。根本就不够用呀。如果把用户随机分成10组,1组做对照,9组做实验,那么只能同时做9组实验。
- 分层实验
- 分层实验:召回、粗排、精排、重排、用户界面、广告..(例如GNN召回通道属于召回层)
- 同层互斥:GNN实验占了召回层的4个桶,其他召回实验只能用剩余的6个桶
- 不同层正交:每一层独立随机对用户做分桶。每一层都可以独立用100%的用户做实验
- 正交是啥?假设上层10%的用户在测试,下层也有10%的用户在测试。由于每一层都是独立随机打散的,意味着受到上层10%影响的用户,在下层也会被随机均匀打散到10个桶中,意味着1/10 * 1/10,只有1%的用户,会同时收到上层+下层的影响,通常来说用户界面实验和召回实验的效果不容易相互增强或者相互抵消,所以这种多层影响是allow的!
- 为什么不能所有都正交,同层也正交呢?
- 如果所有实验都正交,则可以同时做无数组实验。
- 同类的策略(例如精排模型的两种结构)天然互斥,对于一个用户,只能用其中一种。
- 同类的策略(例如添加两条召回通道)效果会相互增强(1+1>2)或相互抵消(1+1<2)。互斥可以避免同类策略相互干扰。
- 不同类型的策略(例如添加召回通道、优化粗排模型),通常不会相互干扰(1+1=2),可以作为正交的两层。
Holdout机制(查收推荐部门,整体性能提升的时候用的,不能简单叠加各层收益昂)
每个实验(召回、粗排、精排、重排)独立汇报对业务指标的提升。但是公司考察一个部门(比如推荐系统)在一段时间内对业务指标总体的提升。因此需要Holdout机制来考察。
取 10% 的用户作为holdout桶,推荐系统使用剩余 90% 的用户做实验,两者互斥。10% holdout 桶 vs 90% 实验桶的diff(需要归一化)为整个部门的业务指标收益。
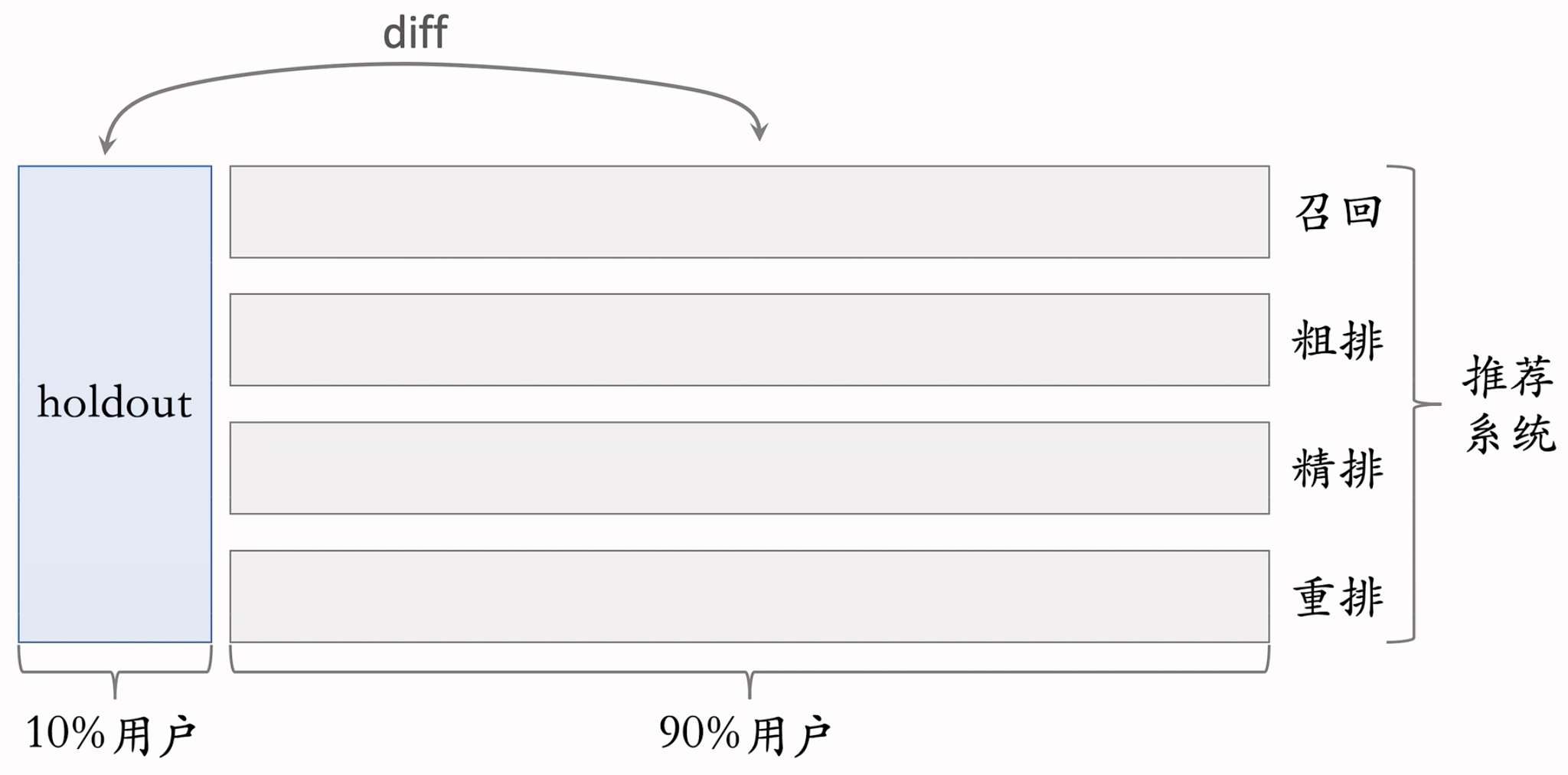
每个考核周期结束之后,清除holdout桶,让推全实验从 90% 用户扩大到 100% 用户。
重新随机划分用户,得到holdout桶和实验桶开始下一轮考核周期。新的holdout桶与实验桶各种业务指标的diff接近0,随着召回、粗排、精排、重排实验上线和推全,diff会逐渐扩大。
推全

- 例如在重排中,如果在10%的用户上,可以提高1%Holdout和实验桶的diff。推全后,这个diff就会扩大至九倍。和A/B test得到的结论一致。注意这里是新建了一层,新的这层会与其他层正交昂!!!
反转实验
有的指标(,点击、交互)立刻收到新策略影响,有的指标(留存)有滞后性,需要长期观测。
实验观测到显著收益后尽快推全新策略。目的是腾出桶供其他实验使用,或需要基于新策略做后续的开发。
用反转实验解决上述矛盾,既可以尽快推全,也可以长期观测实验指标在推全的新层中开一个旧策略的桶,长期观测实验指标。

在推全的过程中,留一部分用户保持原样用于长期对比。可以在类似于清除holdout桶的时候,完成反转桶的清理。
总结
- 分层实验:同层互斥,不同层正交。把容易相互增强(或抵消)的实验放在同一层,让它们的用户互斥
- Holdout: 保留10%的用户,完全不受实验影响,可以考察整个部门对业务指标的贡献。
- 实验推全:新建一个推全层,与其他层正交
- 反转实验:在新的推全层上,保留一个小的反转桶,使用引旧策略。长期观测新旧策略的dff
Recall
ItemCF
Concept
- 思想:
- I love A.
- A is similar with B(I haven’t watched B before.)
- I love B.
- 一个case:
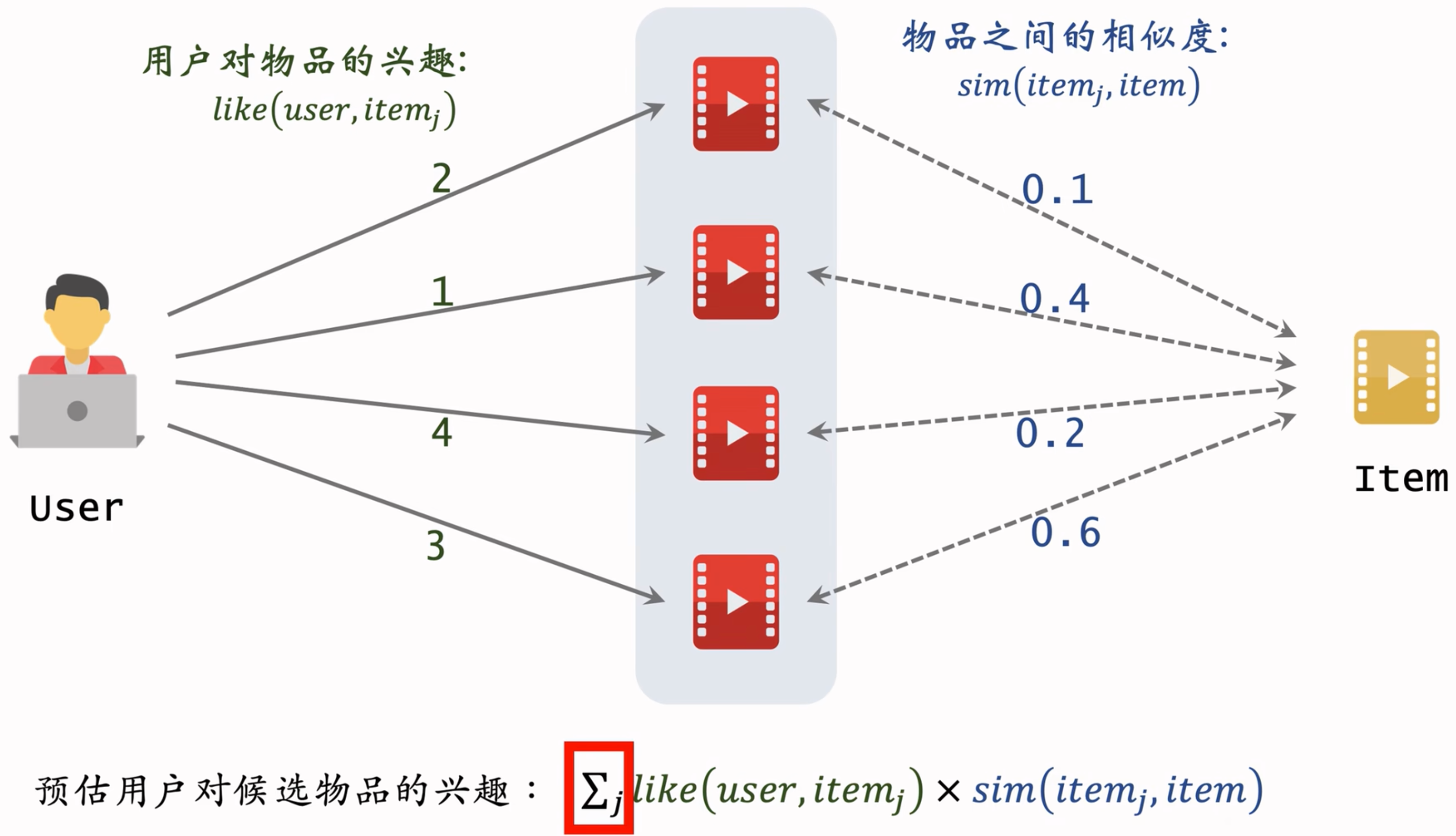
在上面这幅图中,就是每条路径上的like和similarity相乘,再把不同路径的值都想加。
物品相似度如何判断?
两个物品的受众重合度越高,两个物品越相以。例如:喜欢《射雕英雄传》和《神雕侠侣》的读者重合度很高,可以认为《射雕英雄传》和《神雕侠侣》相似。本质上就是沟通Item -> User的倒排关系,然后根据不同的Item的User集合的关系,判断“受众重合度”。
计算相似度公式:
喜欢$i_1$的用户集合:$$\mathcal{W}_1$$
喜欢$i_2$的用户集合:$$\mathcal{W}_2$$
交集:$$\mathcal{V}=\mathcal{W}_1\cap\mathcal{W}_2$$
不考虑物品的喜欢程度的情况下,喜欢就是1,不喜欢就是0,公式为:$$sim(i_1,i_2)=\frac{|\mathcal{V}|}{\sqrt{|\mathcal{W}_1|·|\mathcal{W}_2|}}$$
如果考虑喜欢程度的话,我们在意的“受众重合度”,因此公式里面,用于计算的也是交集中的受众:$$sim(i_1, i_2) = \frac{\sum_{v\in{\mathcal{V}}}like(v, i_1)\ .\ like(v, i_2)}{\sqrt{\sum_{u_1\in\mathcal{W_1}}like^2(u_1, i_1)}\sqrt{\sum_{u_2\in\mathcal{W_2}}like^2(u_2, i_2)}}$$
本质就是余弦相似度hhhh,得到一个0-1之间的分数。
ItemCF的基本思想:
- 如果用户喜欢物品item1,而且物品item1与item2相似,那么用户很可能喜欢物品item2。
- 从用户历史行为记录中,我们知道用户对itemj的兴趣,还知道itemj与候选物品的相似度。
- 每个物品表示为一个稀疏向量,向量每个元素对应一个用户,相似度 sim 就是两个向量夹角的余弦。
Recall Process
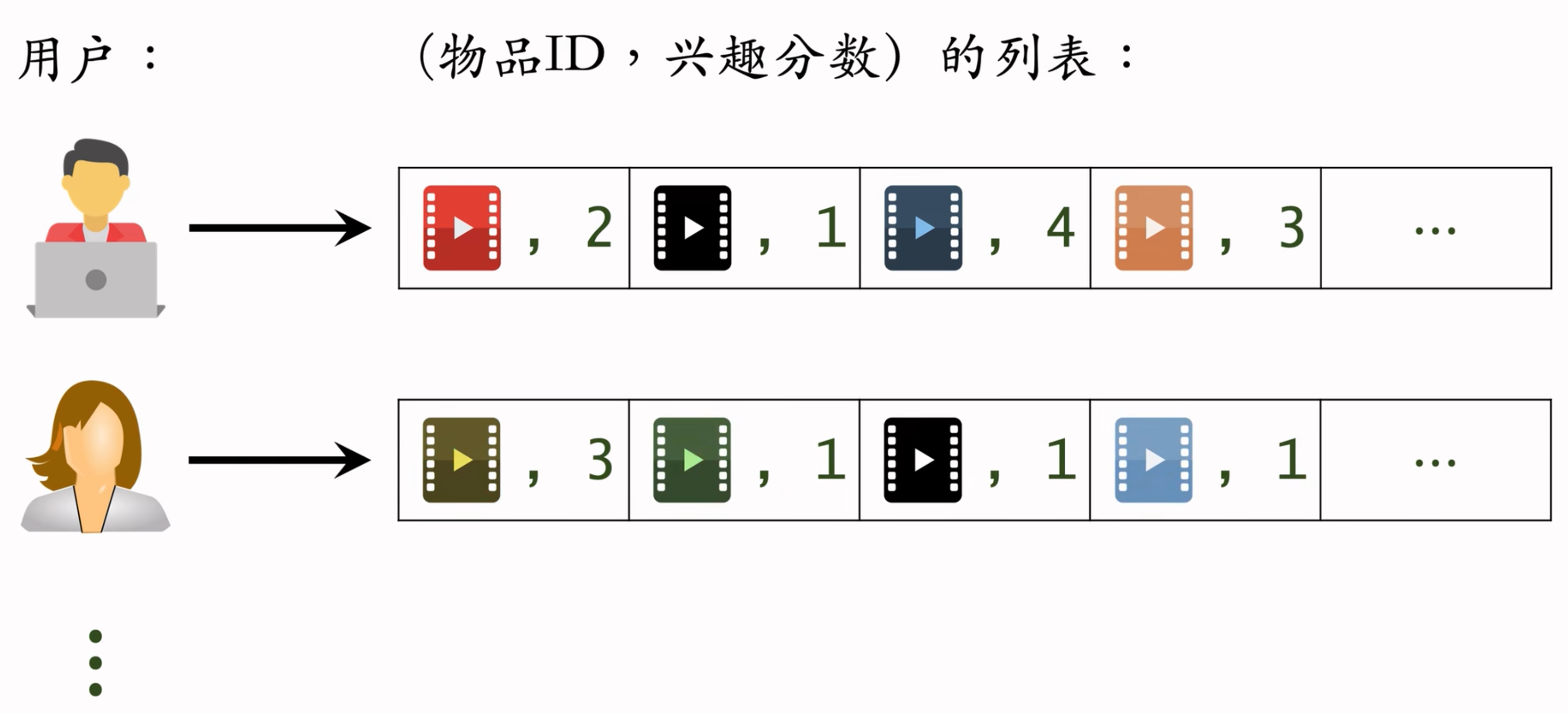
建立 “用户→物品” 的索引
记录每个用户最近点击、交互过的物品D
给定任意用户D,可以找到他近期感兴趣的物品列表
建立 “物品→物品” 的索引(计算量较大)
计算物品之间两两相似度
对于每个物品,索引它最相似的k个物品
给定任意物品D,可以快速找到它最相似的k个物品

线上召回
- 给定用户D,通过“用户→物品”索引,找到用户近期感兴趣的物品列表(last-n)
- 对于last-n列表中每个物品,通过“物品→物品”的索引,找到top-k相似物品
- 对于取回的相似物品(最多有k个),用公式预估用户对物品的兴趣分数
- 返回分数最高的100个物品,作为推荐结果
索引的意义在于避免枚举所有的物品。用索引,离线计算量大,线上计算量小。
- 记录用户最近感兴趣的m=200个物品
- 取回每个物品最相似的k=10个物品
- 给取回的k=2000个物品打分(用户对物品的兴趣)
- 返回分数最高的100个物品作为ItemCF通道的输出
Top-k相似:
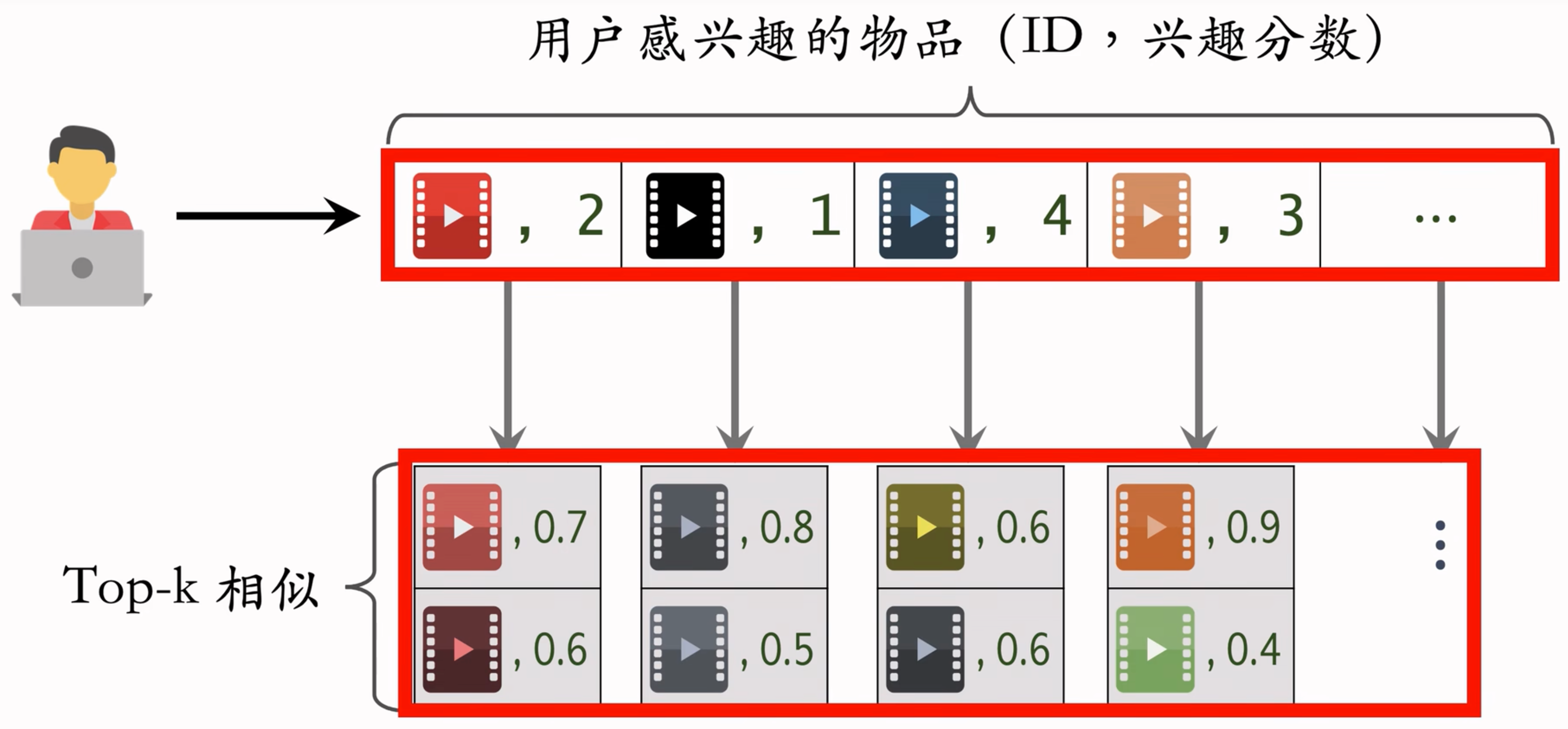
- 取回的 item 中有重复的,就去重,并把分数加起来
Swing
Swing是ItemCF的一个变体,在工业界很常用。Swing和ItemCF很像,唯一区别在于如何定义相似度。
ItemCF的不足之处:如果重合的用户是一个小圈子
两篇笔记被碰巧分享到了一个微信群里面,造成问题:两篇笔记的受众完全不同,但很多用户同时交互过这两篇笔记,导致系统错误判断两篇笔记相似度很高。
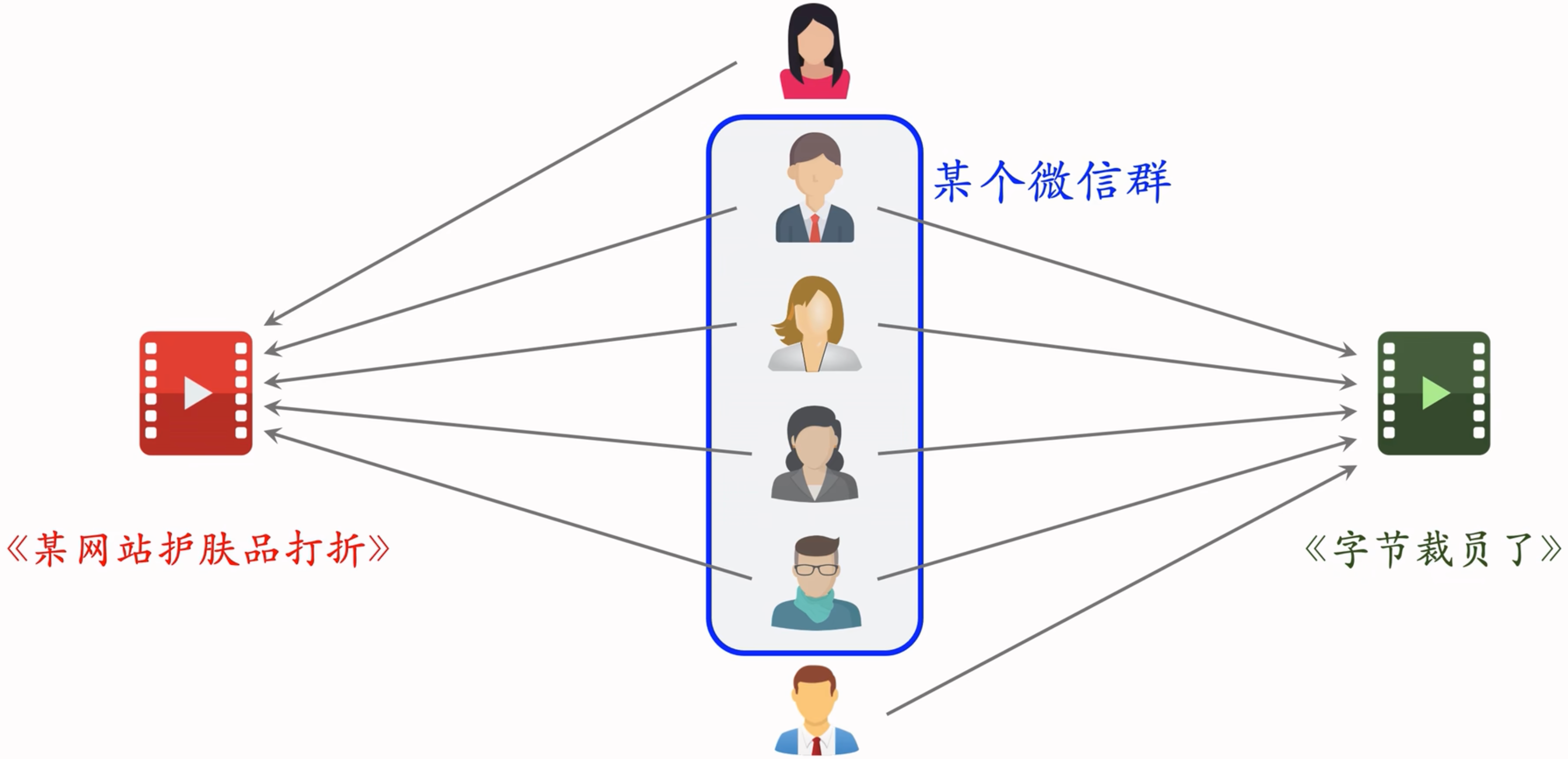
受众完全不一样,但是因为小圈子,导致很多相同的用户交互过这两篇完全受众不同的笔记。导致笔记的相似度被系统错判。认为两篇笔记完全相同。
解决该问题,就要降低小圈子用户的权重。少量相关用户交互不同的物品,说服力较低。但大量不相关的用户同时交互两个物品,则说明两个物品的受众真的相同。
建模:
- 用户 $$u_1$$ 喜欢的物品记作集合 $$\mathcal{J}_1$$
- 用户 $$u_2$$ 喜欢的物品记作集合 $$\mathcal{J}_2$$
- 两个用户的重合度:$$overlap(u_1,u_2)=|\mathcal{J}_1\cap\mathcal{J}_2|$$
- $$u_1 和 u_2 $$的重合度高,则他们可能来自一个小圈子,要降低他们的权重
- 喜欢物品 $$i_1$$ 的用户记作集合 $$\mathcal{W}_1$$
- 喜欢物品 $$i_2$$ 的用户记作集合 $$\mathcal{W}_2$$
- 定义交集 $$\mathcal{V}=\mathcal{W}_1\cap\mathcal{W}_2$$
- 两个物品的相似度:$sim(i_1,i_2)=\sum_{u_1\in \mathcal{V}}\sum_{u_2\in \mathcal{V}}\frac{1}{α+overlap(u_1,u_2)}$
- $α$ 是超参数
- $overlap(u_1,u_2)$ 表示两个用户的重合度
- 重合度高,说明两人是一个小圈子的,那么他两对物品相似度的贡献就比较小
- 重合度小,两人不是一个小圈子的,他两对物品相似度的贡献就比较大
Summary
- Swing 与 ItemCF 唯一的区别在于物品相似度
- ItemCF:两个物品重合的用户比例高,则判定两个物品相似
- Swing:额外考虑重合的用户是否来自一个小圈子
- 同时喜欢两个物品的用户记作集合 $\mathcal{V}$
- 对于 $\mathcal{V}$ 中的用户 $u_1$ 和 $u_2$,重合度记作 $overlap(u_1,u_2)$
- 两个用户重合度大,则可能来自一个小圈子,权重降低
UserCF
Concept
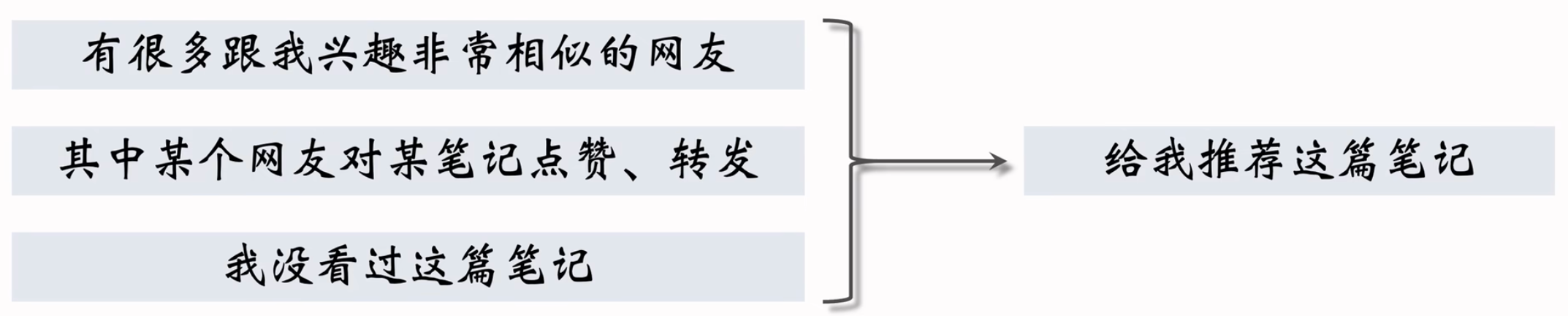
- 找和我相似的用户,推荐我没看过的,他们看过的笔记。
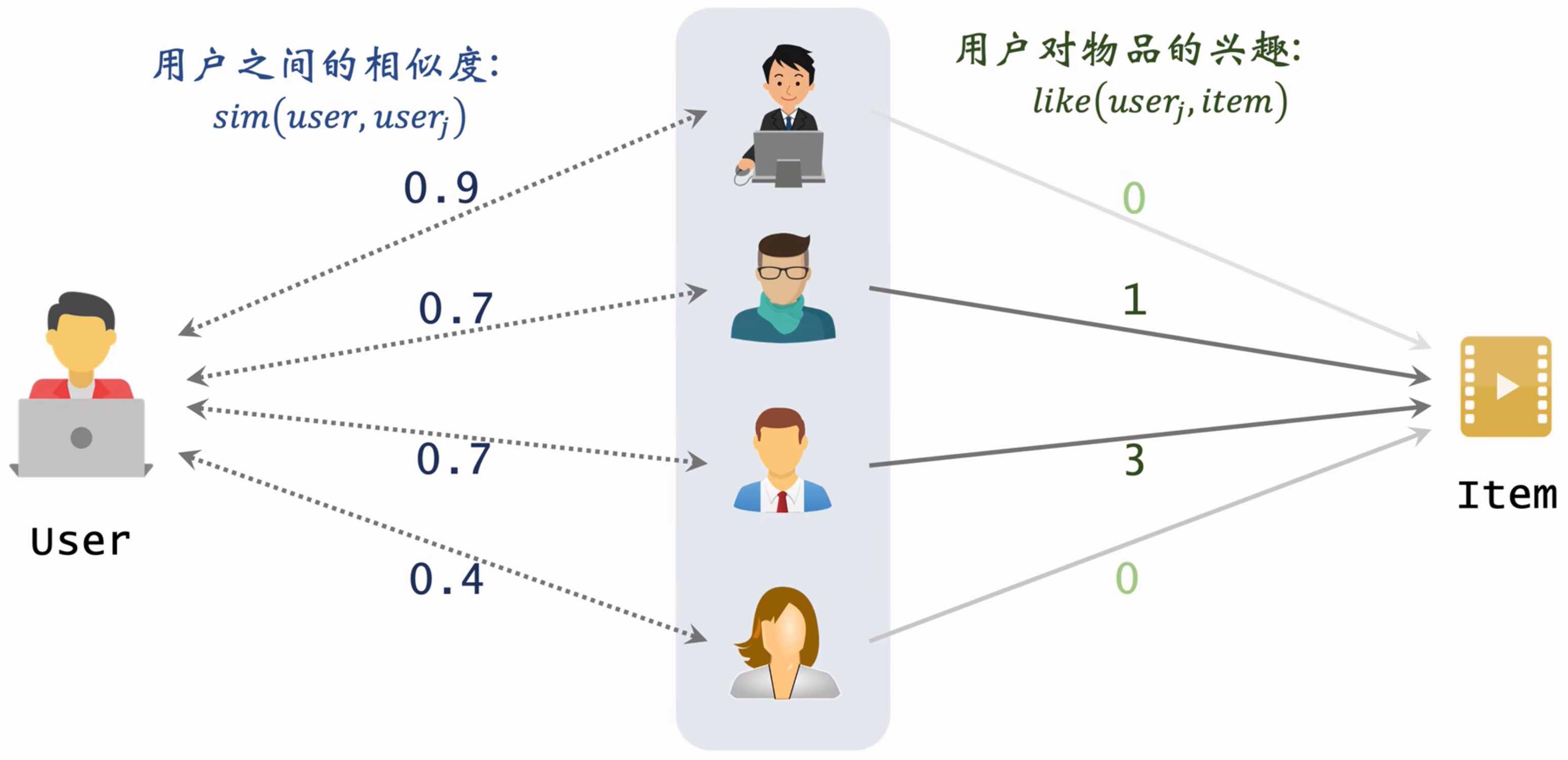
预估用户对候选物品的兴趣:$$\sum_jsim(user,user_j)×like(user_j,item)$$
如何计算用户相似度?
用户 $u_1$ 喜欢的物品记作集合 $\mathcal{J}_1$
用户 $u_2$ 喜欢的物品记作集合 $\mathcal{J}_2$
定义交集 $I=\mathcal{J}_1\cap\mathcal{J}_2$
两个用户的相似度:$sim(u_1,u_2)=\frac{|I|}{\sqrt{|\mathcal{J}_1|·|\mathcal{J}_2|}}$
之前的公式中,交集意味着,交集中的每一个元素,都是同等的权重(为1)。降低热门物品的权重,热门的大家都喜欢看,没那么相似,如何去掉热门物品呢?
降低热门物品权重后:$sim(u_1,u_2)=\frac{{\sum_{l\in{I}} \frac{1}{\log{(1+n_l)}}}}{\sqrt{|\mathcal{J}_1|·|\mathcal{J}_2|}}$
分子中的$n_l$代表的是喜欢商品 l 的用户数量,反映物品的热门程度。
物品越热门,$\frac{1}{\log{(1+n_l)}}$ 越小,对相似度的贡献就越小。
Recall Process
事先做离线计算
建立“用户 → 物品”的索引
记录每个用户最近点击、交互过的物品 ID
给定任意用户 ID,可以找到他近期感兴趣的物品列表
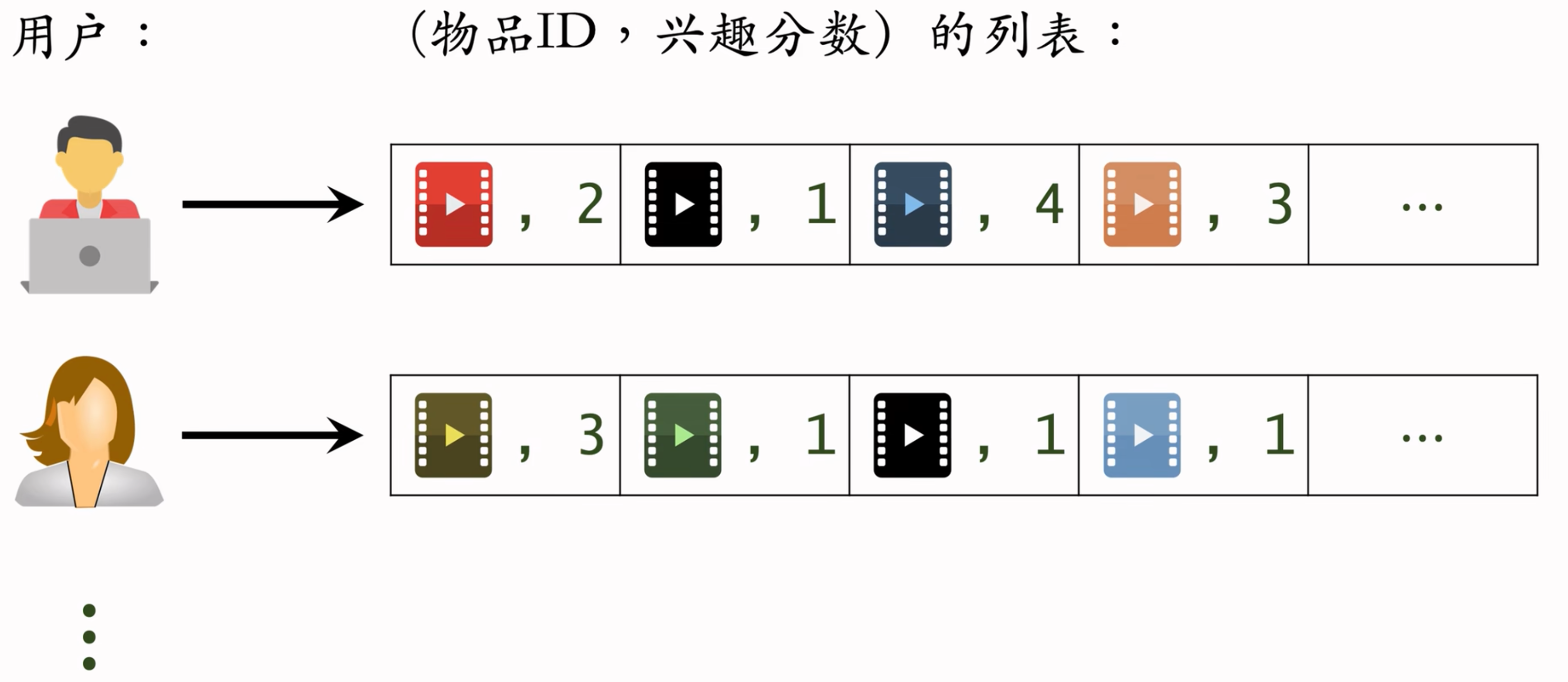
建立“用户 → 用户”的索引(计算量大)
对于每个用户,索引他最相似的 k 个用户
给定任意用户 ID,可以快速找到他最相似的 k 个用户

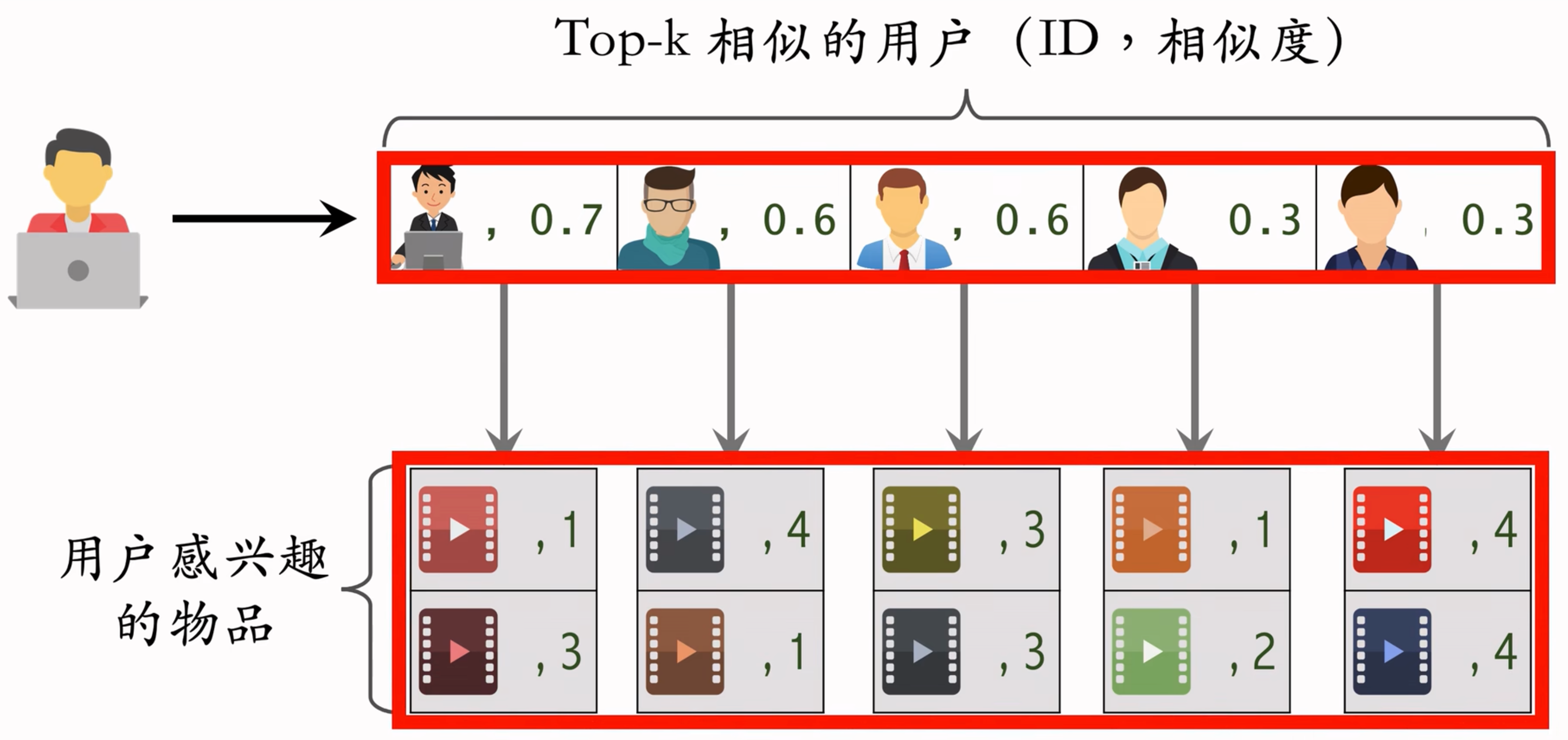
线上做召回
给定用户 ID,通过“用户 → 用户”索引,找到 top-k 相似用户
对于每个 top-k 相似用户,通过“用户 → 物品”索引,找到用户近期感兴趣的物品列表(last-n)
对于取回的 $nk$ 个相似物品,用公式预估用户对每个物品的兴趣分数
返回分数最高的 100 个物品,作为召回结果
Vector Recall Pre Knowledge
Discrete feature processing
处理过程
- 建立字典:类别 -> 序号。
- 向量化:序号映射为向量。
- One-hot编码:把序号映射成高维稀疏向量。
- Embedding:把序号映射成低维稠密向量。
One-hot:
男女:男 -> 1,女 -> 2。未知 -> [0, 0],男 -> [0, 1],女 -> [1, 0]。
国籍:200维表示。中国 -> 1,美国 -> 2,印度 -> 3。未知 -> 0 -> [0, 0, … , 0],中国 -> 1 -> [1, 0, … , 0],美国 -> 2 -> [0, 1, … , 0],印度 -> 3 -> [0, 0, 1, … , 0]
局限:
- 单词编码,几万太大了。笔记有几亿篇,向量超大。类别数量太大时,通常不用one-hot编码。
Embedding:
国籍:中国 -> 1,美国 -> 2,…。Embedding映射为低维向量,例如4 x 1。
参数数量:向量维度 x 类别数量。例如4 x 1的矩阵,总共200个国家,因此总共的参数数量就是4 x 200 = 800个向量(每个国家一个单独的嘛!)。
输入是美国的序号2,输出是一个vector,对应整个4 x 200的参数矩阵的第二列。可以使用Pytorch之类的库实现哈。
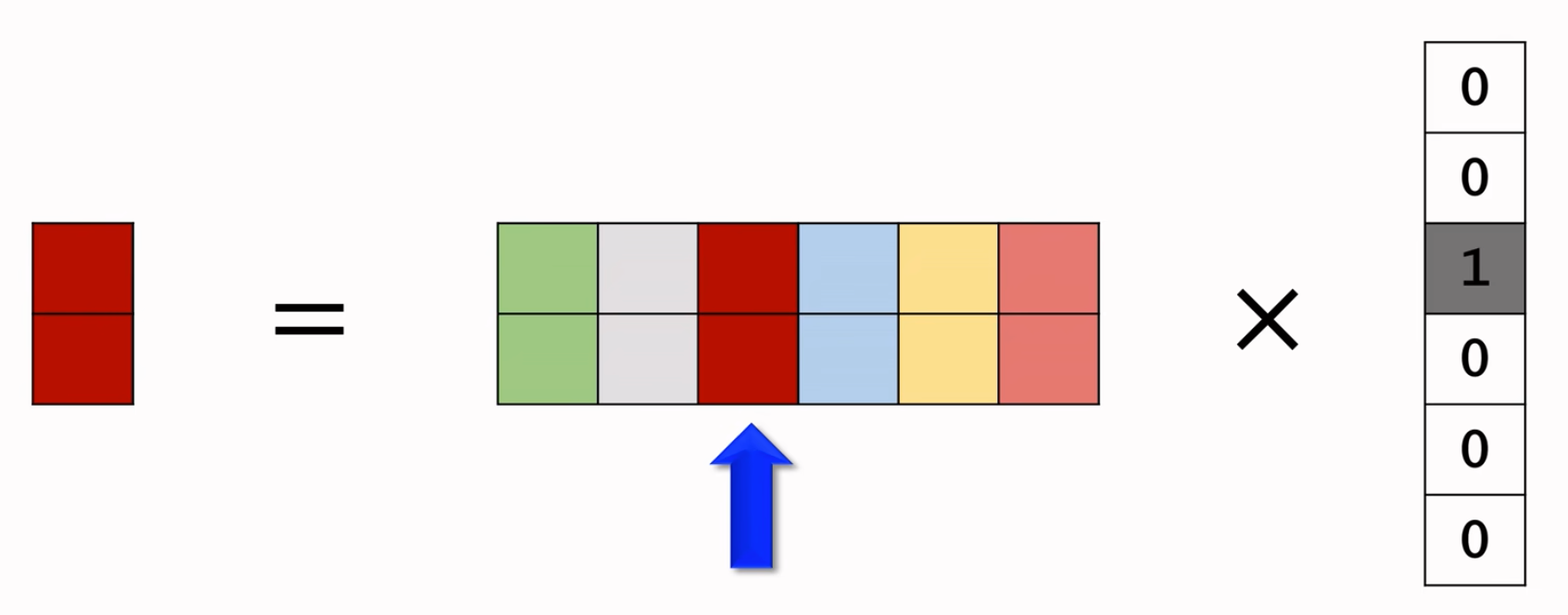
Embedding本质就是:参数矩阵 x One-hot vector,本质就是在一个大参数矩阵中,把你对应的那一列给抽取出来!
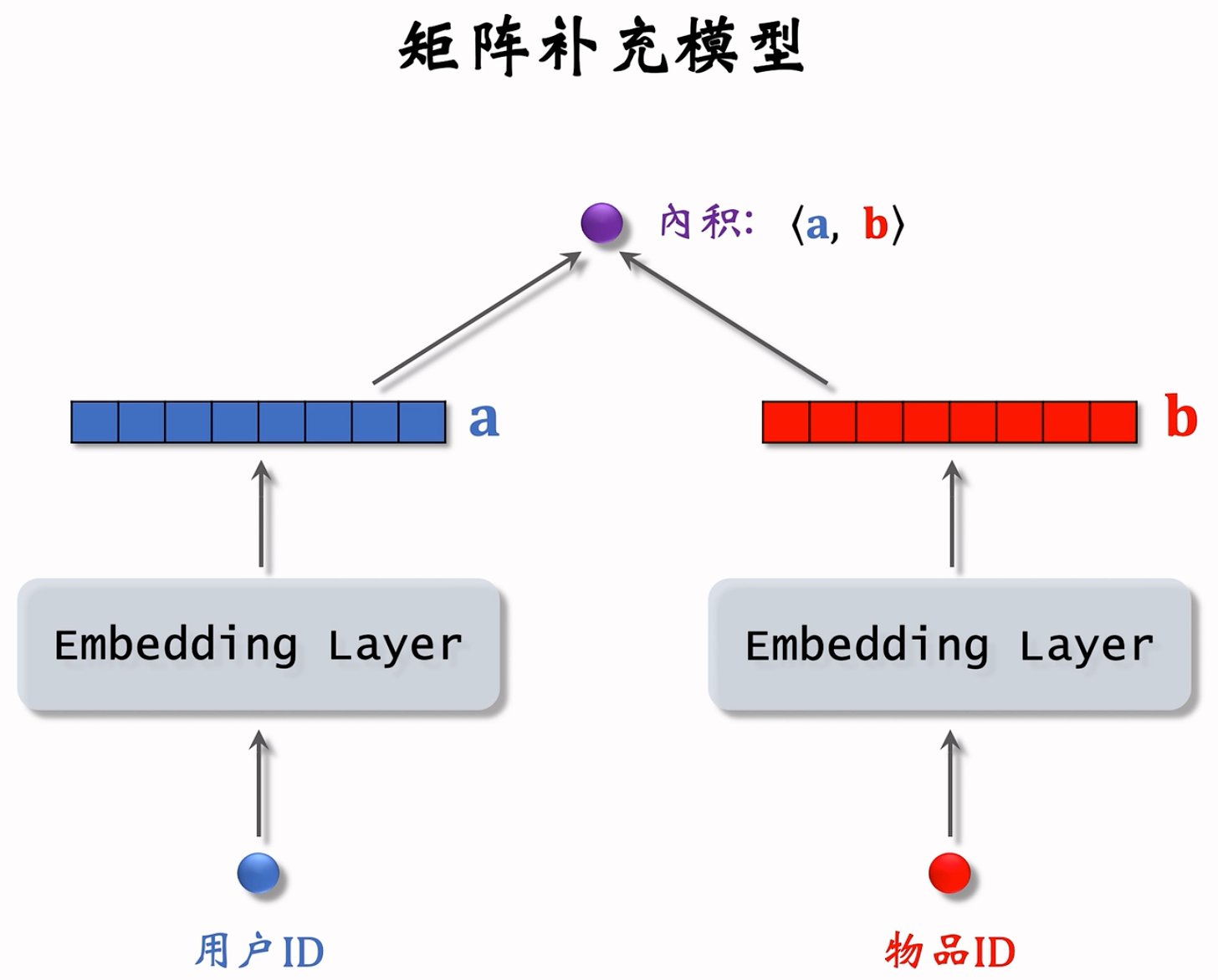
Matrix Completion
训练(这一块儿与传统Machine Learning并无区别)
- 基本想法
- 用户 embedding 参数矩阵记作 $\bold{A}$。第 $u$ 号用户对应矩阵第 $u$ 列,记作向量 $\bold{a}_u$
- 物品 embedding 参数矩阵记作 $\bold{B}$。第 $i$ 号物品对应矩阵第 $i$ 列,记作向量 $\bold{b}_i$
- 内积 $\left\langle \bold{a}_u,\bold{b}_i \right\rangle$ 是第 $u$ 号用户对第 $i$ 号物品兴趣的预估值
- 训练模型的目的是学习矩阵 $\bold{A}$ 和 $\bold{B}$,使得预估值拟合真实观测的兴趣分数
- 数据集
- 数据集:(用户 ID,物品 ID,真实兴趣分数)的集合,记作 $\Omega={(u,i,y) }$
- 数据集中的兴趣分数是系统记录的,比如:
- 曝光但是没有点击 → 0 分
- 点击、点赞、收藏、转发 → 各算 1 分
- 分数最低是 0,最高是 4
- 训练的目的就是让模型的输出拟合真实兴趣分数
- 训练
- 把用户 ID、物品 ID 映射成向量。
- 第 $u$ 号用户 → 向量 $\bold{a}_u$
- 第 $i$ 号物品 → 向量 $\bold{b}_i$
- 求解优化问题,得到参数 $\bold{A}$ 和 $\bold{B}$$\min_{\bold{A},\bold{B}}\sum_{(u,i,y)\in\Omega}(y- \left\langle \bold{a}_u,\bold{b}_i \right\rangle)^2$
- 找到使得 真实兴趣分数 $y$ 与 模型输出 $\left\langle \bold{a}_u,\bold{b}_i \right\rangle$ 间 差别 最小的 $\bold{A}$ 和 $\bold{B}$
- 求最小化常用的方法就是随机梯度下降,每次更新矩阵 $\bold{A}$ 和 $\bold{B}$ 的一列
- 把用户 ID、物品 ID 映射成向量。
- 基本想法
为什么叫做矩阵补充?
- 矩阵是稀疏矩阵,而拿到的神经网络在训练好了之后,则可以对任意User, Item(矩阵中的任意行、任意列做计算/补全)。
- 矩阵中只有少数位置是绿色,大多数位置是灰色(即大部分物品没有曝光给用户)而我们用绿色位置训练出的模型,可以预估所有灰色位置的输出,即把矩阵的元素补全。
- 把矩阵元素补全后,我们只需选出对应用户一行中分数较高的 物品 推荐给 用户 即可。
生产中没有使用,效果不好
- 缺点 1:仅用 ID embedding,没利用物品、用户属性
- 物品属性:类目、关键词、地理位置、作者信息
- 用户属性:性别、年龄、地理定位、感兴趣的类目
- 双塔模型可以看做矩阵补充的升级版,双塔模型不仅使用 ID,还结合各种属性。
- 缺点 2:负样本的选取方式不对
- 样本:用户—物品的二元组,记作 $(u,i)$
- 正样本:曝光之后,有点击、交互。(正确的做法)
- 负样本:曝光之后,没有点击、交互。(错误的做法)
- 缺点 3:做训练的方法不好
- 内积 $\left\langle \bold{a}_u,\bold{b}_i \right\rangle$ 不如余弦相似度。工业界普遍使用余弦相似度而不是内积。
- 用平方损失(回归),不如用交叉熵损失(分类)。
- 缺点 1:仅用 ID embedding,没利用物品、用户属性
Online Service
- 模型存储
- 训练得到矩阵 $\bold{A}$ 和 $\bold{B}$
- $\bold{A}$ 的每一列对应一个用户
- $\bold{B}$ 的每一列对应一个物品
- 把矩阵 $\bold{A}$ 的列存储到 key-value 表
- key 是用户 ID,value 是 $\bold{A}$ 的一列
- 给定用户 ID,返回一个向量(用户的 embedding)
- 矩阵 $\bold{B}$ 的存储和索引比较复杂
- 训练得到矩阵 $\bold{A}$ 和 $\bold{B}$
- 线上服务
- 把用户 ID 作为 key,查询 key-value 表,得到该用户的 embedding 向量,记作 $\bold{a}$
- 最近邻查找:查找用户最有可能感兴趣的 $k$ 个物品,作为召回结果
- 第 𝑖 号物品的 embedding 向量记作 $\bold{b}_i$
- 内积 $\left\langle \bold{a}_u,\bold{b}_i \right\rangle$ 是用户对第 𝑖 号物品兴趣的预估
- 返回内积最大的 $k$ 个物品
- 如果枚举所有物品,时间复杂度正比于物品数量。
- 最近邻查找的计算量太大,不现实,下面讲解如何加速最近邻查找。
Approximate nearest neighbor search
支持最近邻查找的系统
- 系统:Milvus、Faiss、HnswLib、等等,快速最近邻查找的算法已经被集成到这些系统中。
- 衡量最近邻的标准:
- 欧式距离最小(L2 距离)
- 向量内积最大(内积相似度),矩阵补充用的就是内积相似度
- 向量夹角余弦最大(cosine 相似度),最常用
- 对于不支持的系统:把所有向量作归一化(让它们的二范数等于 1),此时内积就等于余弦相似度
数据预处理:把数据据划分为多个区域
- 划分后,每个区域用一个向量表示,这些向量的长度都是 1
- 例如图中蓝色区域用蓝色箭头向量表示
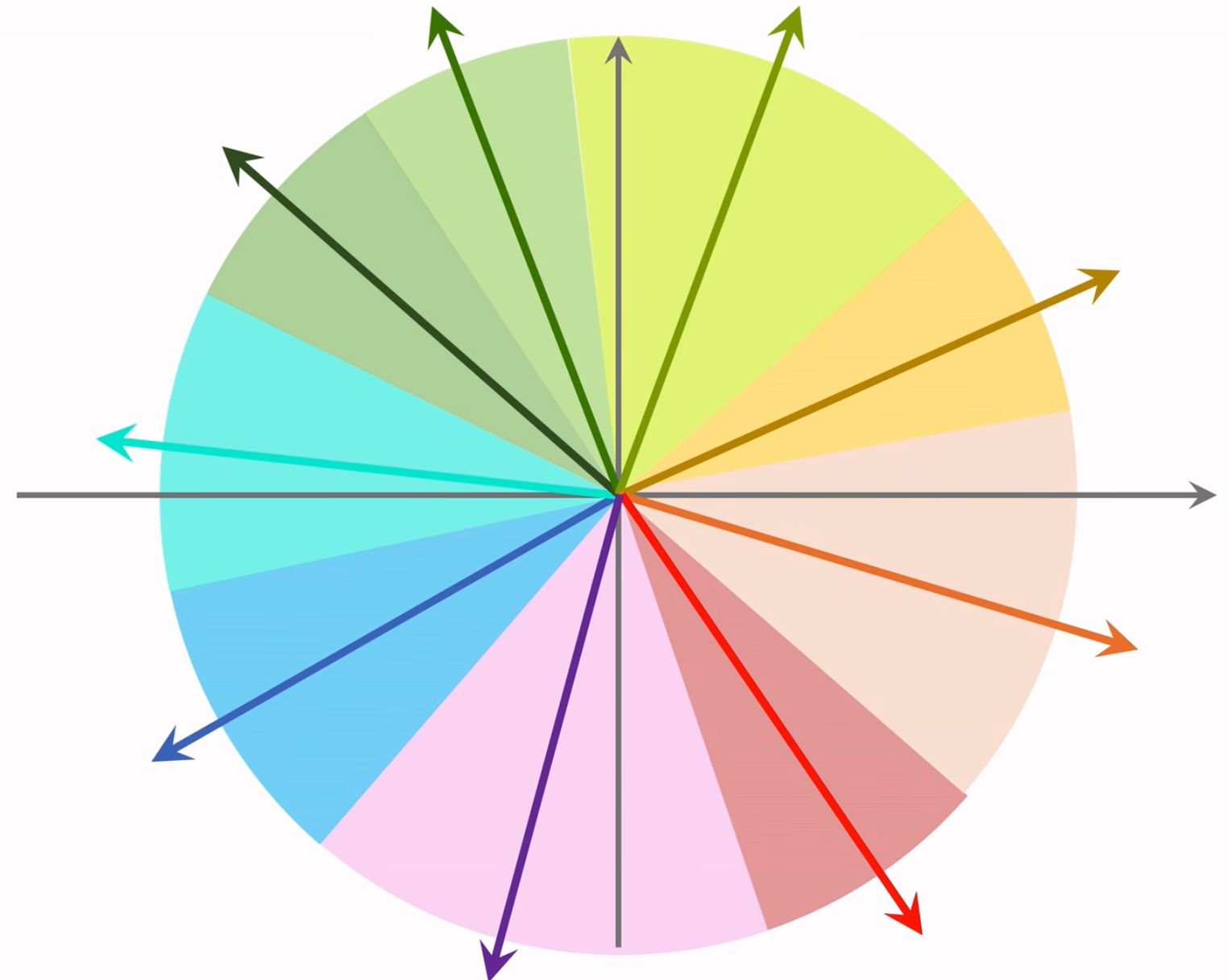
朴素的想法哈哈哈哈,空间换时间,先定区,再去区内查找,就少了很多检索花费的时间啦!比暴力枚举比较好太多了!
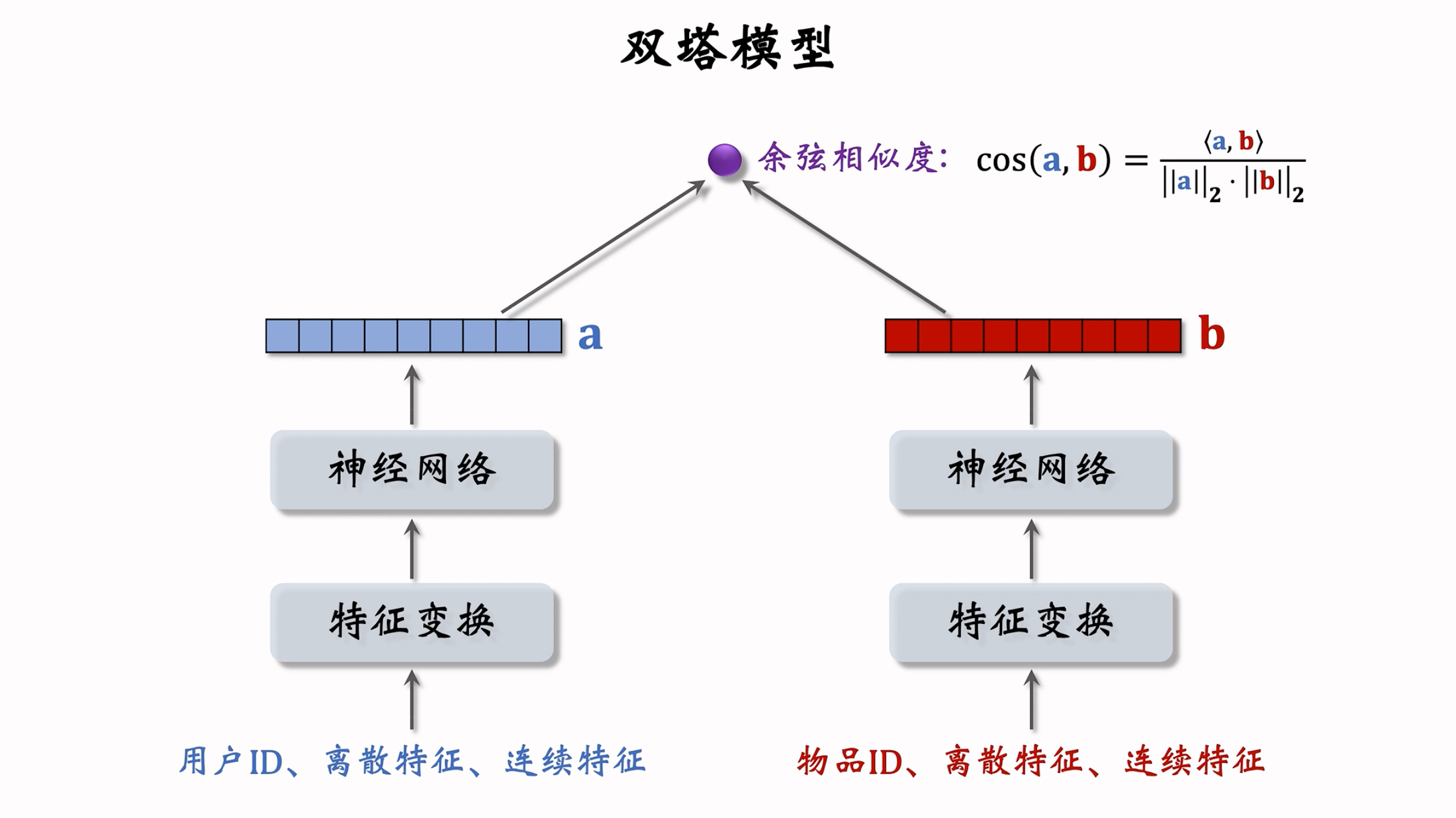
Twin tower model
Concept
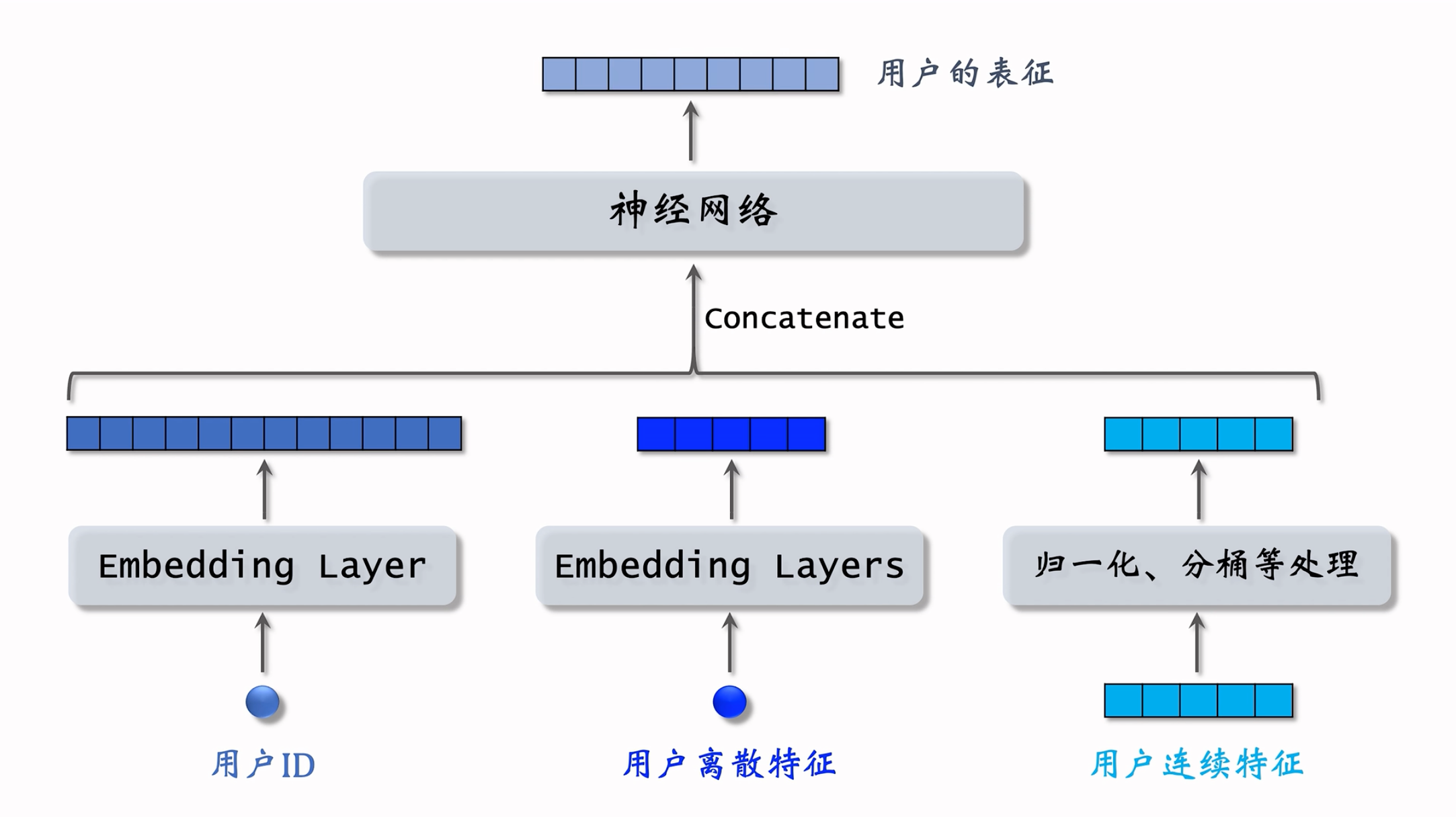
- 用户离散特征:例如所在城市、感兴趣的话题等。
- 对每个离散特征,单独使用一个 Embedding 层得到一个向量。
- 对于性别这种类别很少的离散特征,直接用 one-hot 编码。
- 用户连续特征:年龄、活跃程度、消费金额等,也有对应的处理方法。
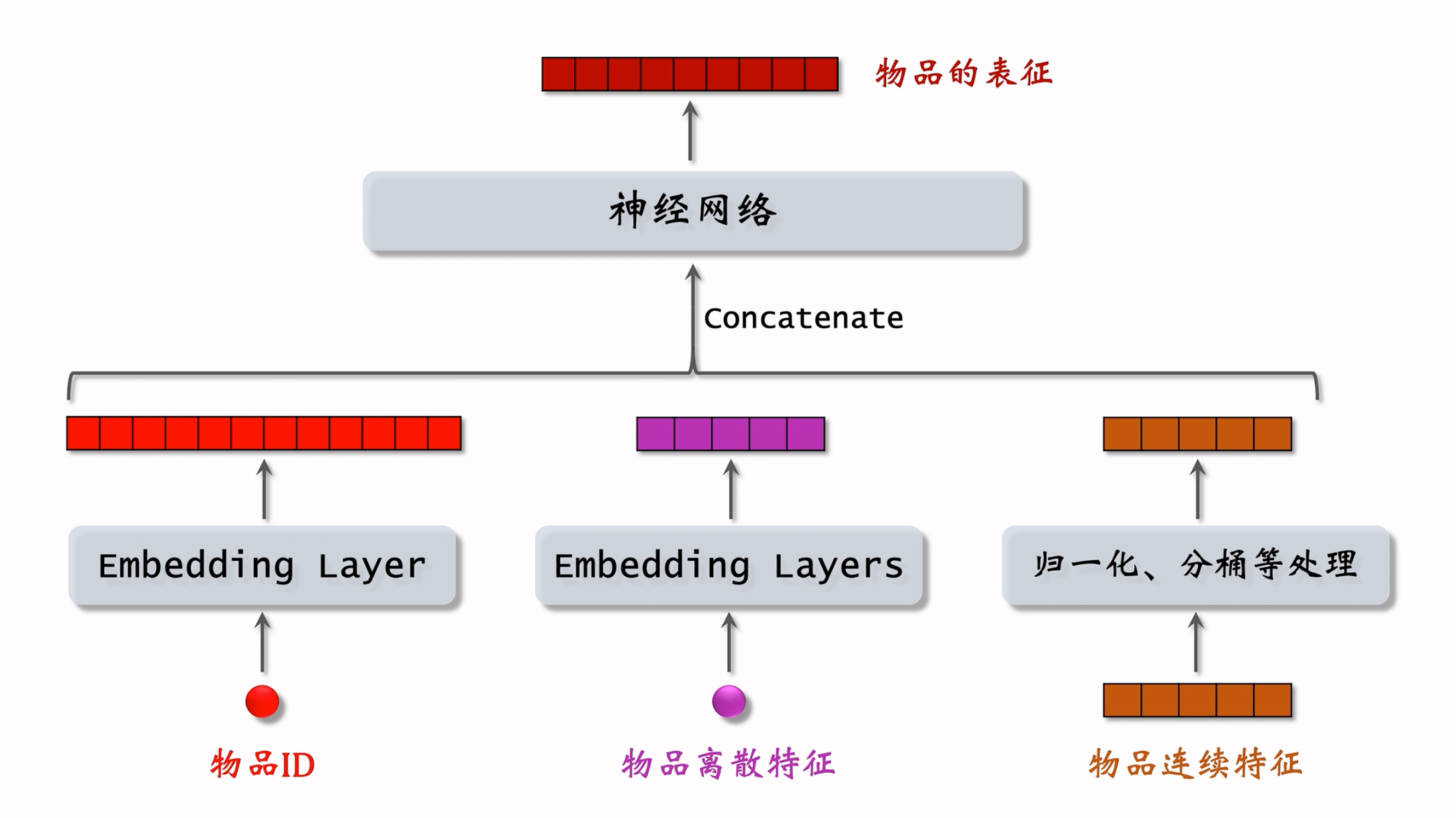
双塔模型:左塔提取用户特征,右塔提取物品特征。与矩阵补充的区别在于,使用了除 ID 外的多种特征作为双塔的输入。
双塔模型的训练
- Pointwise:独立看待每个正样本、负样本,做简单的二元分类
- Pairwise:每次取一个正样本、一个负样本。
- Listwise:每次取一个正样本、多个负样本。
- 正负样本的选择
- 正样本:用户点击的物品
- 负样本可能有很多指标和标准:
- 没有被召回的?
- 召回但是被粗排、精排淘汰的?
- 曝光但是未点击的?
Pointwise
- 把召回看做二元分类任务
- 对于正样本,鼓励 $\cos{(\bold{a},\bold{b})}$ 接近 +1
- 对于负样本,鼓励 $\cos{(\bold{a},\bold{b})}$ 接近 −1
- 控制正负样本数量为 1: 2 或者 1: 3(经验hhhh)
Pairwise
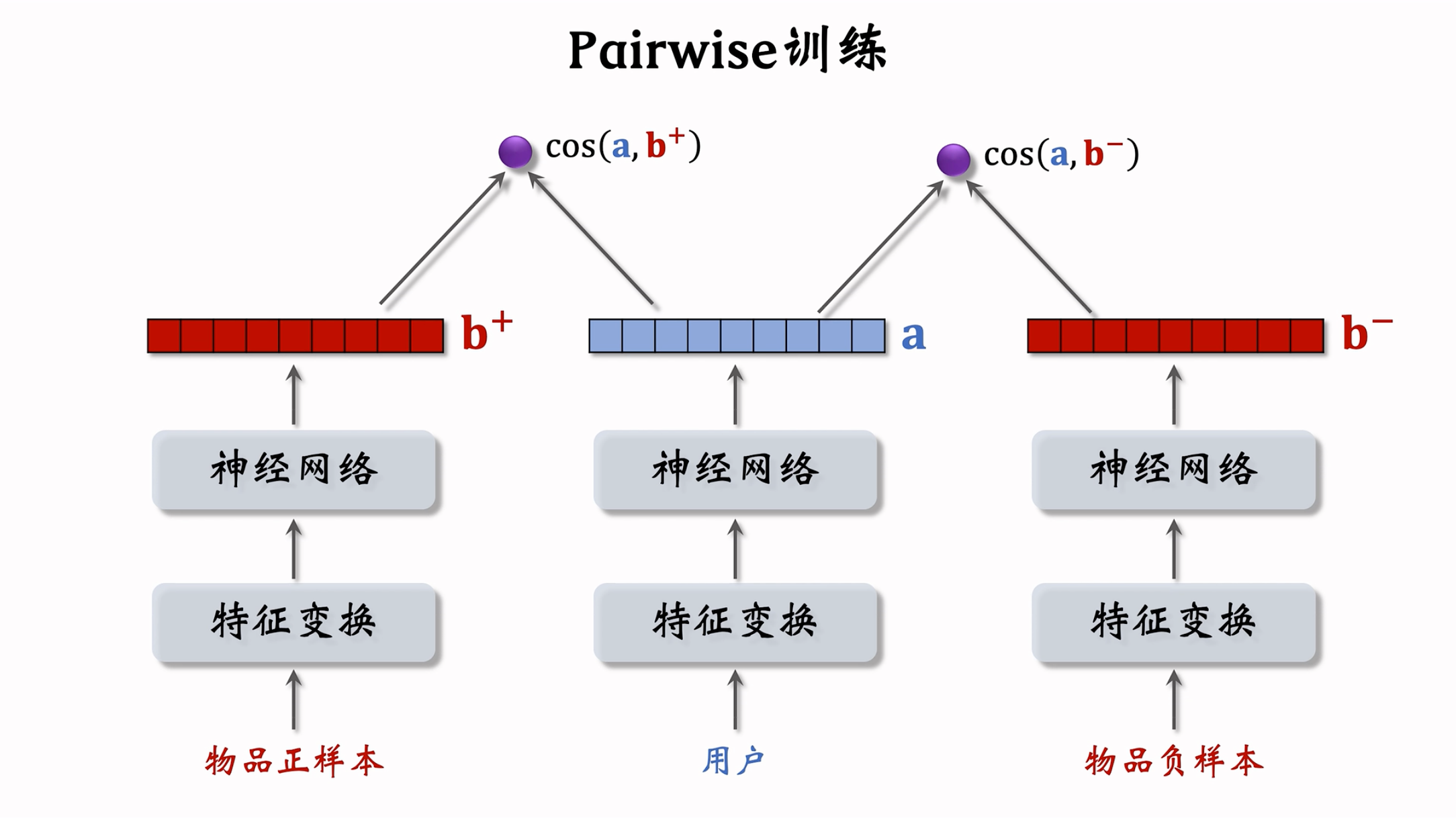
两个物品塔是相同的,它们共享参数。
基本想法:鼓励 $\cos{(\bold{a},\bold{b}^+)}$ 大于 $\cos{(\bold{a},\bold{b}^-)}$,两者只差越大越好!!!
- 如果 $\cos{(\bold{a},\bold{b}^+)}$ 大于 $\cos{(\bold{a},\bold{b}^-)}+m$,则没有损失。 $m$ 是超参数,需要调
- 否则,损失等于 $\cos{(\bold{a},\bold{b}^-)}+m-\cos{(\bold{a},\bold{b}^+)}$
Triplet hinge loss: $L(\bold{a},\bold{b}^+,\bold{b}^-)=\max{\{ 0,\cos{(\bold{a},\bold{b}^-)}+m-\cos{(\bold{a},\bold{b}^+)}\}}$
Triplet logistic loss:
○ Loss function: $L(\bold{a},\bold{b}^+,\bold{b}^-)=\log{( 1+\exp{[\sigma·(\cos{(\bold{a},\bold{b}^-)}-\cos{(\bold{a},\bold{b}^+))}])}}$
○ $\sigma$ 是大于 0 的超参数,控制损失函数的形状,需手动设置
Listwise
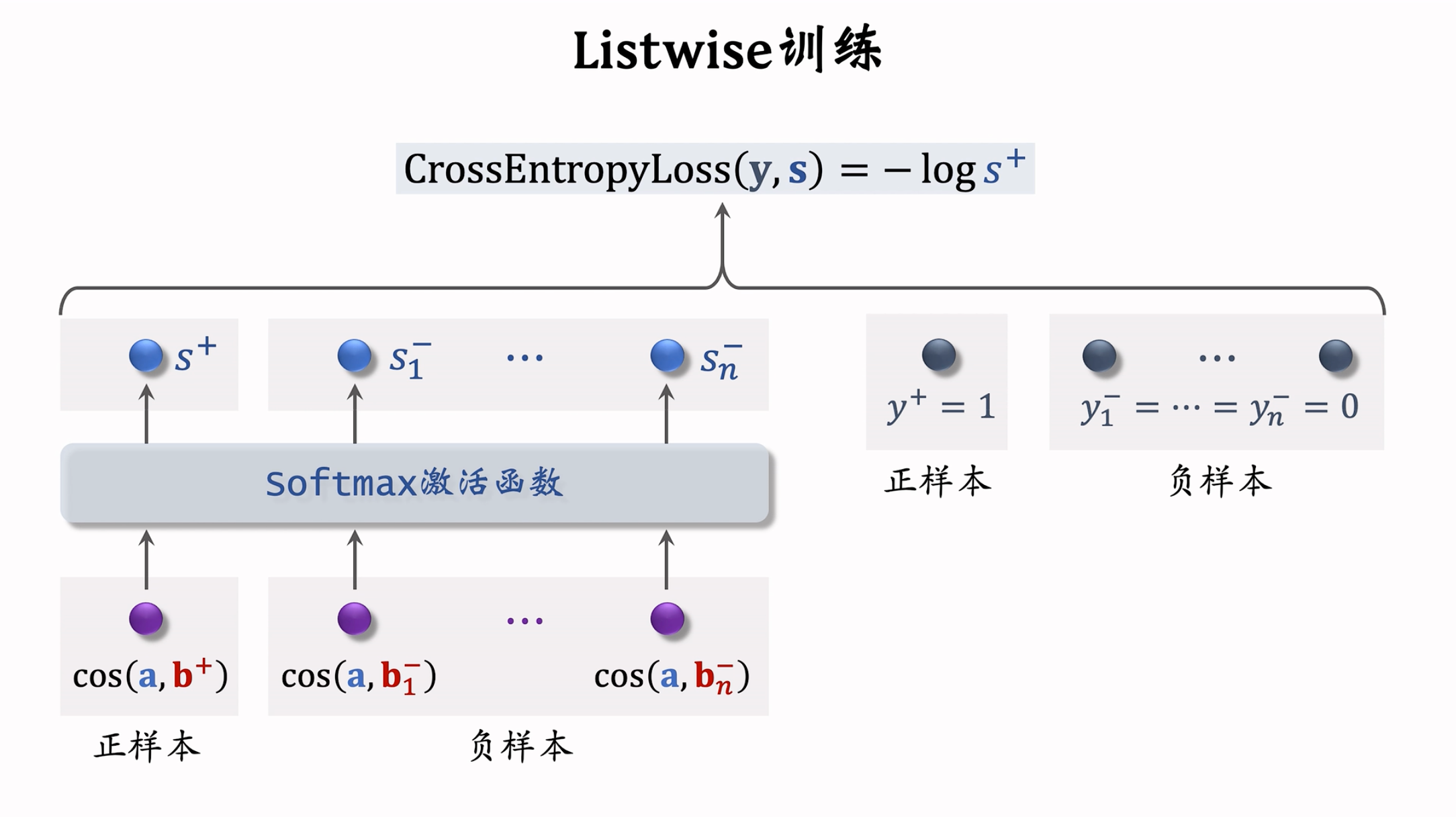
- 一条数据包含:
- 一个用户,特征向量记作 $\bold{a}$
- 一个正样本,特征向量记作 $\bold{b}^+$
- 多个负样本,特征向量记作 $\bold{b}^-_1,…,\bold{b}^-_n$
- 鼓励 $\cos{(\bold{a},\bold{b}^+)}$ 尽量大,鼓励 $\cos{(\bold{a},\bold{b}^-_1)},…,\cos{(\bold{a},\bold{b}^-_n)}$ 尽量小。
- 正样本 $y^+=1$,即鼓励 $s^+$ 趋于 1,负样本 $y^-_1=…=y^-_n=0$,即鼓励 $s^-_1…s^-_n$ 趋于 0,用 $y$ 和 $s$ 的交叉熵作为损失函数,意思是鼓励 $\rm Softmax$ 的输出 $s$ 接近标签 $y$。
- 一条数据包含:
错误的模型设计:
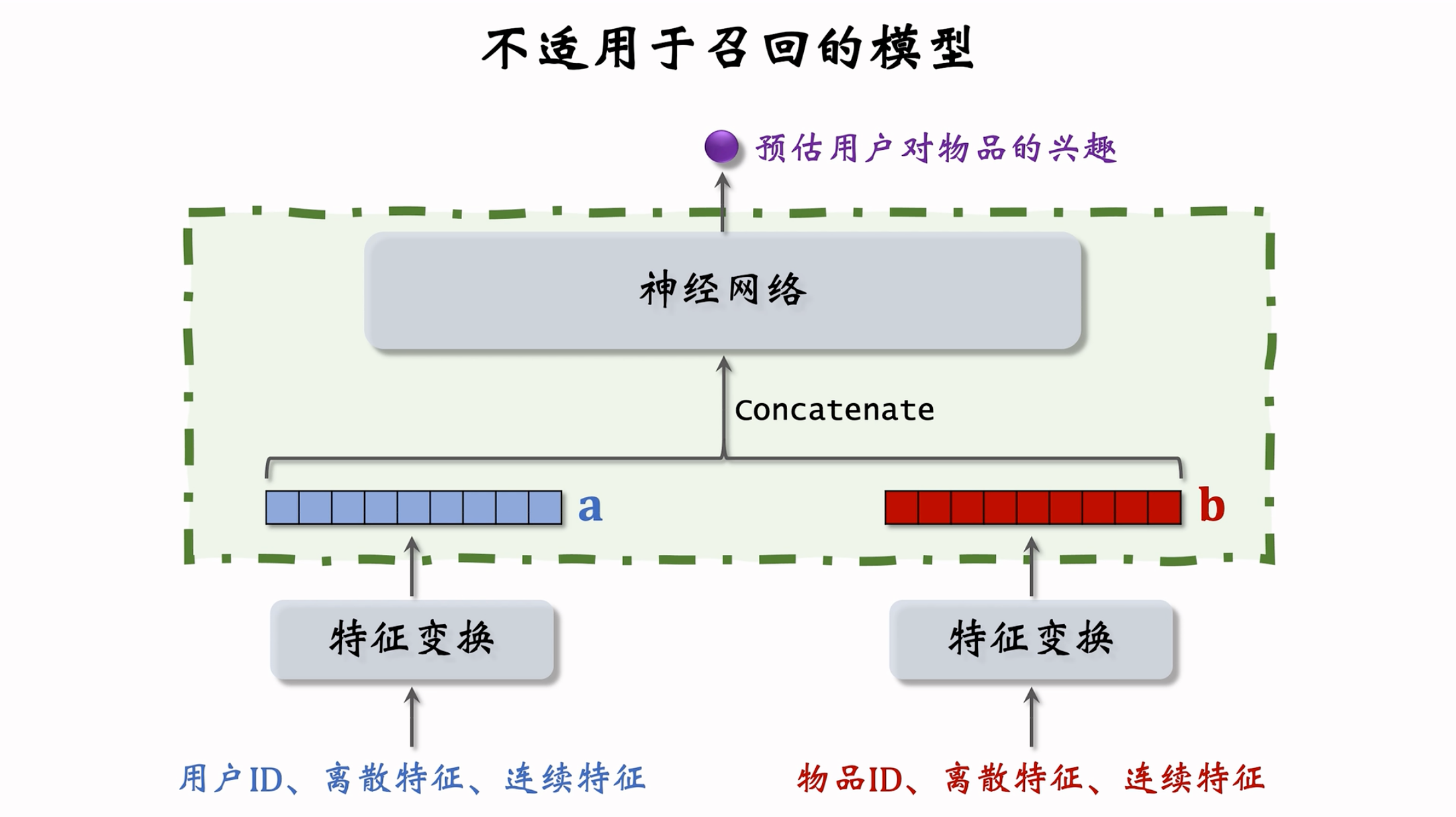
- 用户和物品的向量在进入神经网络前就拼接起来了,和双塔模型有很大区别。
- 双塔模型是在后期输出相似度时才进行融合。
- 用户(或物品)自身特征的拼接没有影响,依然保持了用户(或物品)的独立性。而一旦用户和物品进行拼接,此时的输出就特定于该 用户(或物品)了
- 这种前期融合的模型,不适用于召回
- 因为得在召回前,把每个用户向量对应的所有物品向量挨个拼接了送入神经网络
- 假设有一亿个物品,每给用户做一次召回,就得跑一亿遍。
- 这种模型通常用于排序,在几千个候选物品中选出几百个
- 以后看到这种模型就要意识到 —— 这是排序模型,不是召回模型
- 我的一些thoughts:
- 因为如果是输入后的,保存的是embedding和对应的索引,但是,如果是输入之前的,每次都要重新计算。换句话说,在线推荐的时候,其实在模型参数固定的情况下,用户塔和物品塔拿到的Embedding结果,是可以离线算出来的。在线召回的时候只需要计算“相似度”,这个是很快很快的。但是如果“拼接 + 塞入神经网络”,每次在线召回的时候,对每个用户的所有物品,都要过一次神经网络,这个计算量是很大的。
- 以及,当上面不是神经网络的时候,可以用类似于最似近邻查找的方法。在Embedding的空间中分区分块,快速找到结果。而神经网络杜绝了这种可能性,每次都要一对一重新计算,这个计算量也是很大的。
- 综上:需要遍历的数据量增多 + 每一次计算的时间增长,使得这种模型设计不适用于在线召回。
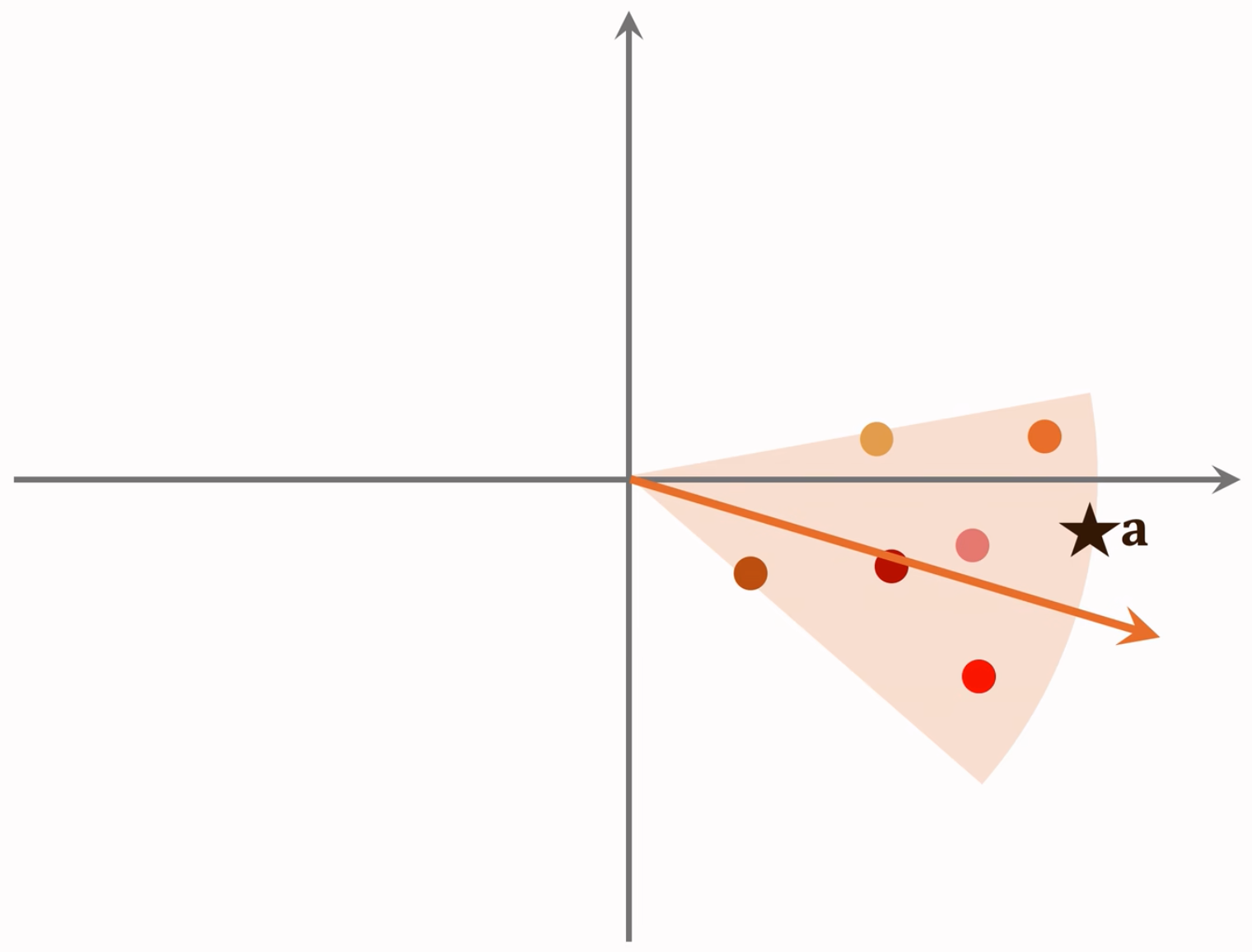
Positive and negative samples
正样本:曝光而且有点击的用户一物品二元组。(用户对物品感兴趣)。问题:少部分物品占据大部分点击’导致正样本大多是热门物品。
解决方案:过采样冷门物品,或降采样热门物品
- 过采样(up-sampling):一个样本出现多次
- 降采样(down-sampling):一些样本被抛弃
如何选择负样本:
简单负样本:全体物品
- 未被召回的物品,大概率是用户不感兴趣的。
- 未被召回的物品约等于全体物品(几亿里面抽取几千个,相当于就是全体物品用户都不care,小概率事件约等于不发生)
- 从全体物品中做抽样,作为负样本。
- 均匀抽样 or 非均匀抽样?
- 均匀抽样:对冷门物品不公平(绝大多数商品都是冷门物品)
- 正样本大多是热门物品。
- 如果均匀抽样产生负样本,负样本大多是冷门物品。
- 结果:热门物品更热,冷门物品更冷。
- 非均抽采样:目的是打压热门物品
- 负样本抽样概率与热门程度(点击次数)正相关。
- 抽样概率 正比于 $(点击次数)^{0.75}$。0.75是经验值。
- 均匀抽样:对冷门物品不公平(绝大多数商品都是冷门物品)
简单负样本:Batch内负样本
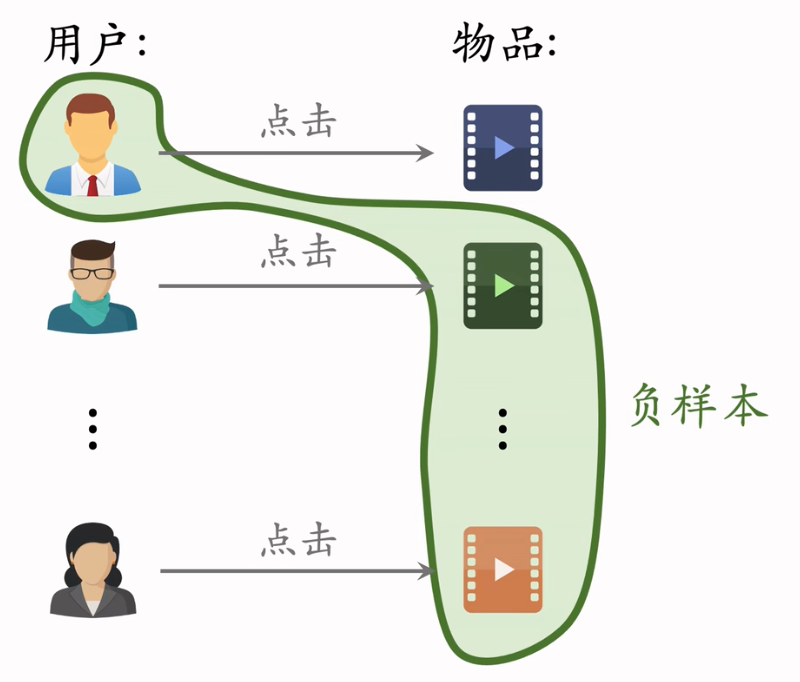
- 用户和自己batch内,自己没有点击的物品构成负样本。一个batch内有n个正样本。一个用户和 n-1 个物品组成负样本。这个batch内一共有 n(n-1) 个负样本。
- 都是简单负样本。(因为第一个用户不喜欢第二个物品。)
- Batch内负样本存在的问题
- 一个物品出现在batch内的概率 正比于 点击次数
- 物品成为负样本的概率本该是正比于点击次数的0.75次方,但这里实际是点击次数。热门物品成为负样本的概率过大,即对热门物品打压太狠了,容易造成偏差。
- 下面这篇论文讲了如何修正偏差:Xinyang Yi et al. Sampling-Bias-Corrected Neural Modeling for Large Corpus Item Recommendations. In RecSys, 2019.
- 修正偏差:
- 物品 i 被抽样到的概率:$p_i$ 正比于 点击次数
- 预估用户对物品 $i$ 的兴趣:$cos(a,b_i)$
- 做训练的时候,将兴趣调整为:$cos(a,b_i)一log\ p_i$
- 这样纠偏,避免过度打压热门物品
- 训练结束后,在线上做召回时,还是用$cos(a,b_i)$作为兴趣
困难负样本:
- 被粗排淘汰的物品(比较困难)
- 这些物品被召回,说明和用户兴趣有关;又被粗排淘汰,说明用户对物品兴趣不大
- 而在对正负样本做二元分类时,这些困难样本容易被分错(被错误判定为正样本)
- 精排分数靠后的物品(非常困难)
- 能够进入精排,说明物品比较符合用户兴趣,但不是用户最感兴趣的
- 对正负样本做二元分类:
- 全体物品(简单)分类准确率高
- 被粗排淘汰的物品(比较困难)容易分错
- 精排分数靠后的物品(非常困难)更容易分错
- 被粗排淘汰的物品(比较困难)
训练数据
- 混合几种负样本
- 50% 的负样本是全体物品(简单负样本)
- 50% 的负样本是没通过排序的物品(困难负样本)—> 即在粗排、精排淘汰的物品
常见错误:把曝光但是没有点击的样本作为负样本
工业界已经踩过雷,并且作为教训。
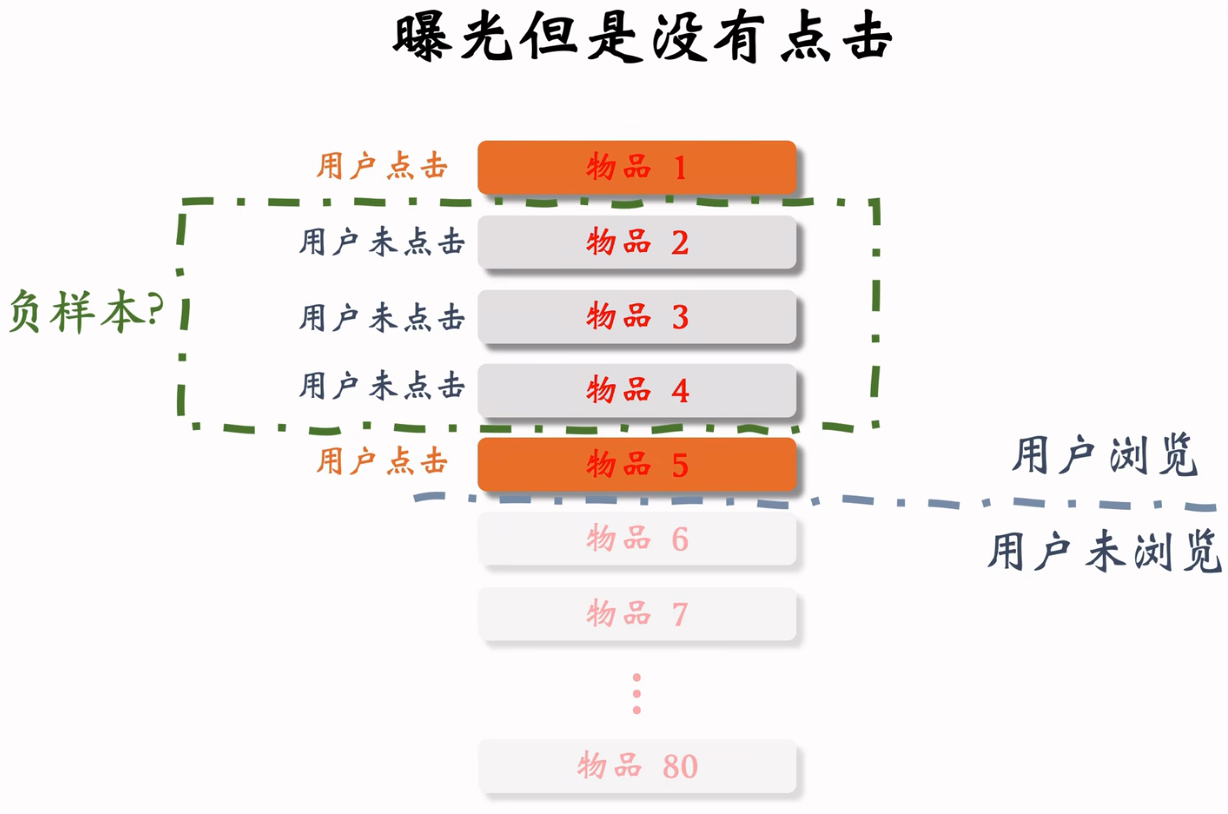
训练召回模型不能用这类负样本。训练排序模型才能用这类负样本。
选择负样本的原理:
- 召回的目标:快速找到用户可能感兴趣的物品。即区分用户 不感兴趣 和 可能感兴趣 的物品,而不是区分 比较感兴趣 和 非常感兴趣 的物品
- 全体物品(easy ):绝大多数是用户根本不感兴趣的。
- 被排序淘汰(hard ):用户可能感兴趣,但是不够感兴趣。
- 有曝光没点击(没用):用户感兴趣,可能碰巧没有点击
- 曝光没点击的物品已经非常符合用户兴趣了,甚至可以拿来做召回的正样本。
- 可以作为排序的负样本,不能作为召回的负样本。
Online recalls and updates
线上召回:
双塔模型的召回
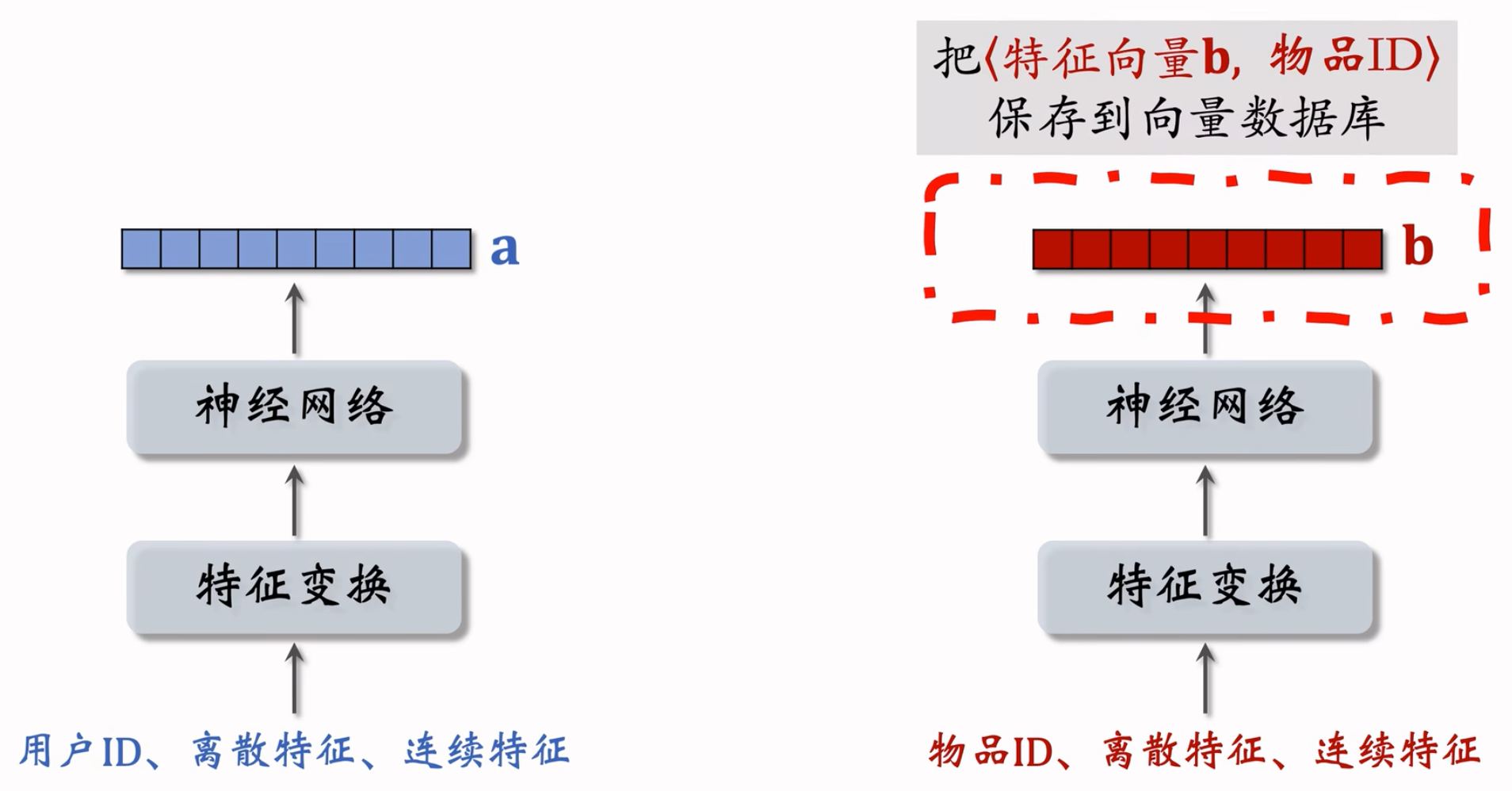
离线存储:把物品向量 $\bold{b}$ 存入向量数据库
完成训练之后,用物品塔计算每个物品的特征向量 $\bold{b}$
把几亿个物品向量 $\bold{b}$ 存入向量数据库(比如 Milvus、Faiss、HnswLib )
向量数据库建索引,以便加速最近邻查找
线上召回:查找用户最感兴趣的 $k$ 个物品
给定用户 ID 和画像,线上用神经网络现算(实时计算)用户向量 $\bold{a}$。
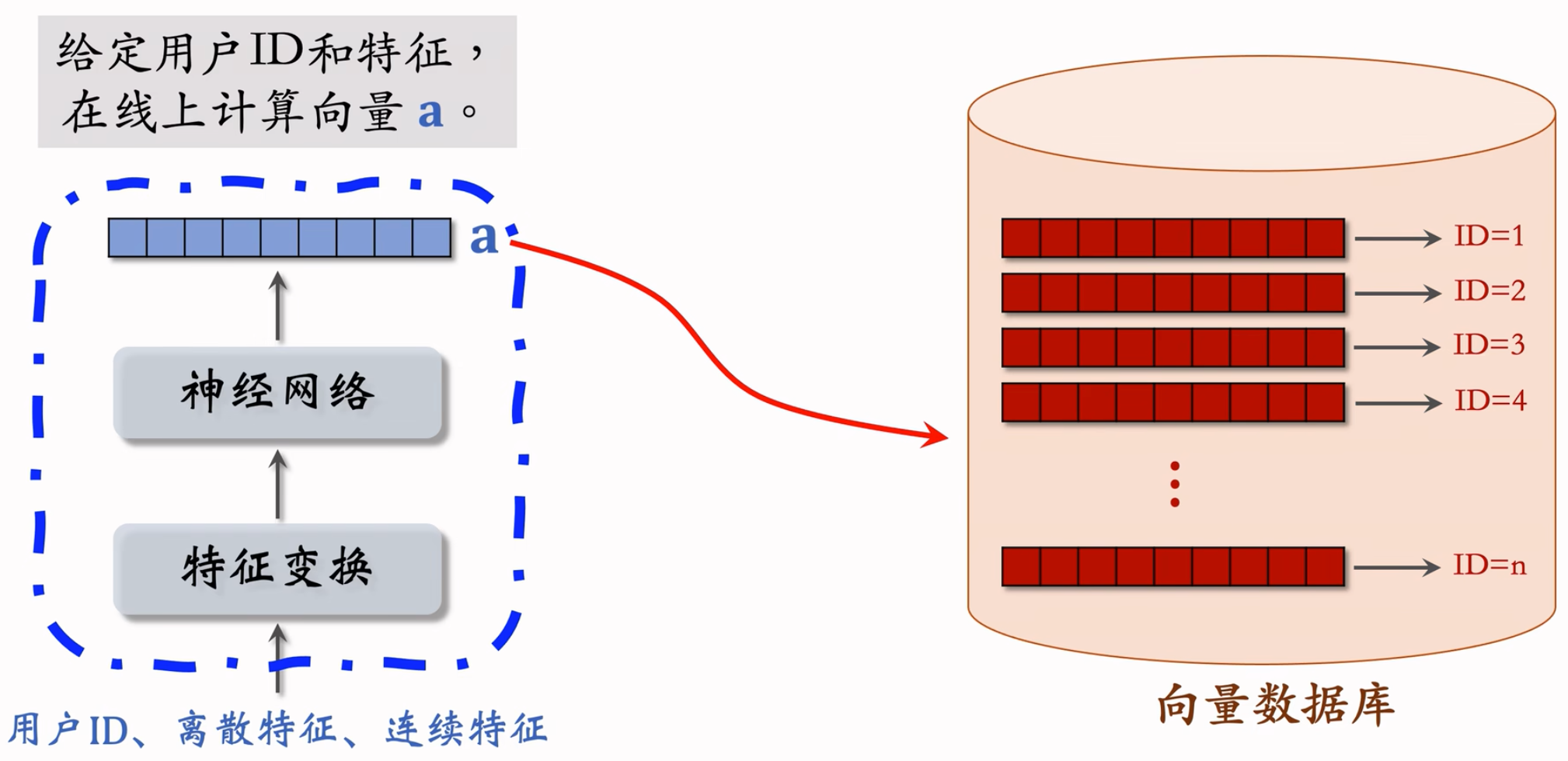
最近邻查找:
- 把向量 $\bold{a}$ 作为 query,调用向量数据库做最近邻查找
- 返回余弦相似度最大的 $k$ 个物品,作为召回结果
为什么事先存储物品向量 $\bold{b}$,线上现算用户向量 $\bold{a}$?
- 为了拿到用户的实时特征啊,离线存储可能推的就不是用户当前喜欢的了,物品特征变化很小或者不变,但是用户特征变化很快
- 每做一次召回,用到一个用户向量 $\bold{a}$,几亿物品向量 $\bold{b}$(线上算物品向量的代价过大)
- 用户兴趣动态变化,而物品特征相对稳定(可以离线存储用户向量,但不利于推荐效果)
模型更新
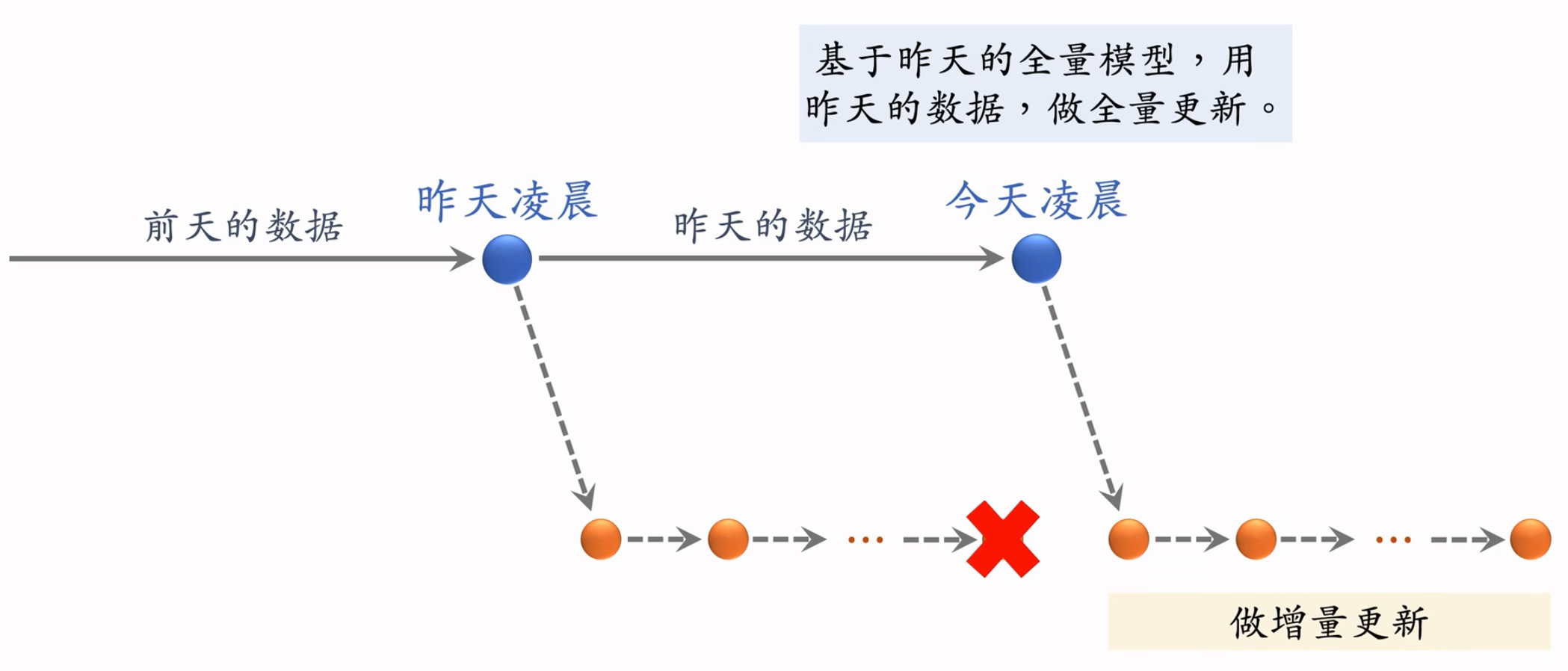
全量更新
- 全量更新:每天凌晨,用昨天全天的数据训练模型
- 在昨天模型参数的基础上做训练(不是重新随机初始化)
- 用昨天的数据,训练 1 epoch,即每天数据只用一遍
- 发布新的 用户塔神经网络 和 物品向量,存入向量数据库并建立索引。供线上召回使用
- 全量更新对数据流、系统的要求比较低。不需要实时数据流,对数据生成速度没有要求,延迟一两个小时也没关系。只需要凌晨批处理就行。每天只发布一次,对系统要求也低。
增量更新:
- 做 online learning 更新模型参数,用户兴趣会随时发生变化。小时级别的增量更新,对数据流和系统要求都很高,实时收集线上数据,做流式处理,生成 TFRecord 文件。
- 对模型做 online learning,增量更新 ID Embedding 参数(不更新神经网络其他部分的参数)。即锁住全连接层的参数,只更新 Embedding 层的参数,只有全量更新才更新全连接层,这是出于工程实现的考量。
- 发布用户 ID Embedding,供用户塔在线上计算用户向量,最新的ID Embedding会捕捉到用户最新的兴趣点,对推荐很有帮助。 -> 其实用户的ID Embedding变了,在Item Embedding空间中的位置就变了,最近邻搜索到的结果就会不一样昂!
双管齐下:
- 可以只增量,不全量吗?
- 试过了,效果不好。小时级数据有偏;分钟级数据偏差更大。
- 增量更新:按照数据从早到晚的顺序,做1 epoch训练。
- 全量更新:random shuffle一天的数据,做1 epoch训练。(Shuffle就是为了消除偏差)随机打乱优于按顺序排列数据,全量训练优于增量训练。
- 可以试试分钟学ID,小时学全部特征嵌入,但不学神经网络,按天学神经网络。
- 可以只增量,不全量吗?
Summmary
双塔模型
- 用户塔、物品塔各输出一个向量,两个向量的余弦。相似度作为兴趣的预估值。
- 三种训练的方式:pointwise pairwise、listwise。
- 正样本:用户,点击过的物品。
- 负样本:全体物品(简单)、被排序淘汰的物品(困难)
召回
- 做完训练,把物品向量存储到向量数据库,供线上最近邻查找。
- 线上召回时,给定用户D、用户画像,调用用户塔,现算用户向量a。
- 把a作为query,查询向量数据库,找到余弦相似度最高的k个物品向量,返回k个物品ID。
更新模型
- 全量更新:今天凌晨,用昨天的数据训练整个神经网络,做1 epoch的随机梯度下降。
- 增量更新:用实时数据训练神经网络,只更新ID Embedding,锁住全连接层。
- 实际的系统:
- 全量更新 & 增量更新相结合。
- 每隔几十分钟,发布最新的用户ID Embedding,供用户塔在线上计算用户向量。
Twin Tower + Self-supervised Learning
自监督学习的目的:把物品塔训练的更好。
双塔模型的问题
推荐系统的头部效应严重:
- 少部分物品占据大部分点击。
- 大部分物品的点击次数不高。
高点击物品的表征学得好,长尾物品的表征学得不好。
自监督学习:做data augmentation,更好地学习长尾物品的向量表征。
参考:Tiansheng Yao et al.Self-supervised Learning for Large-scale Item Recommendations. In CIKM,2021.
Listwise Training
训练方式
Listwise上面提到过,一个Batch里面,一个用户自己感兴趣的为正样本,和其他用户感兴趣的构成负样本。
- 一个batch包含正样本:$(a_1, b_1), (a_2, b_2), … , (a_n, b_n)$
- 负样本${(a_i, b_j)}$,对于所有的i不等于j。
- 训练的时候,鼓励$cos(a_i, b_i)$尽量大,鼓励$cos(a_i, b_j)$尽量小。
损失函数:
纠偏:
Batch类负样本会过度打压负样本,要纠偏。
物品j被抽样到的概率$p_j$正比于点击次数。做训练的时候,预估用户 i 对物品 j 的兴趣:$cos(a_i, b_j) - log\ p_{j}$,训练结束后,在线上做召回的时候则不用纠偏,直接用余弦相似度即可。
参考:Xinyang Yi et al.Sampling-Bias-Corrected Neural Modeling for Large
Corpus Item Recommendations.In RecSys,2019.
训练双塔模型:
- 从点击数据中随机抽取个用户一物品二元组,组成一个batch。
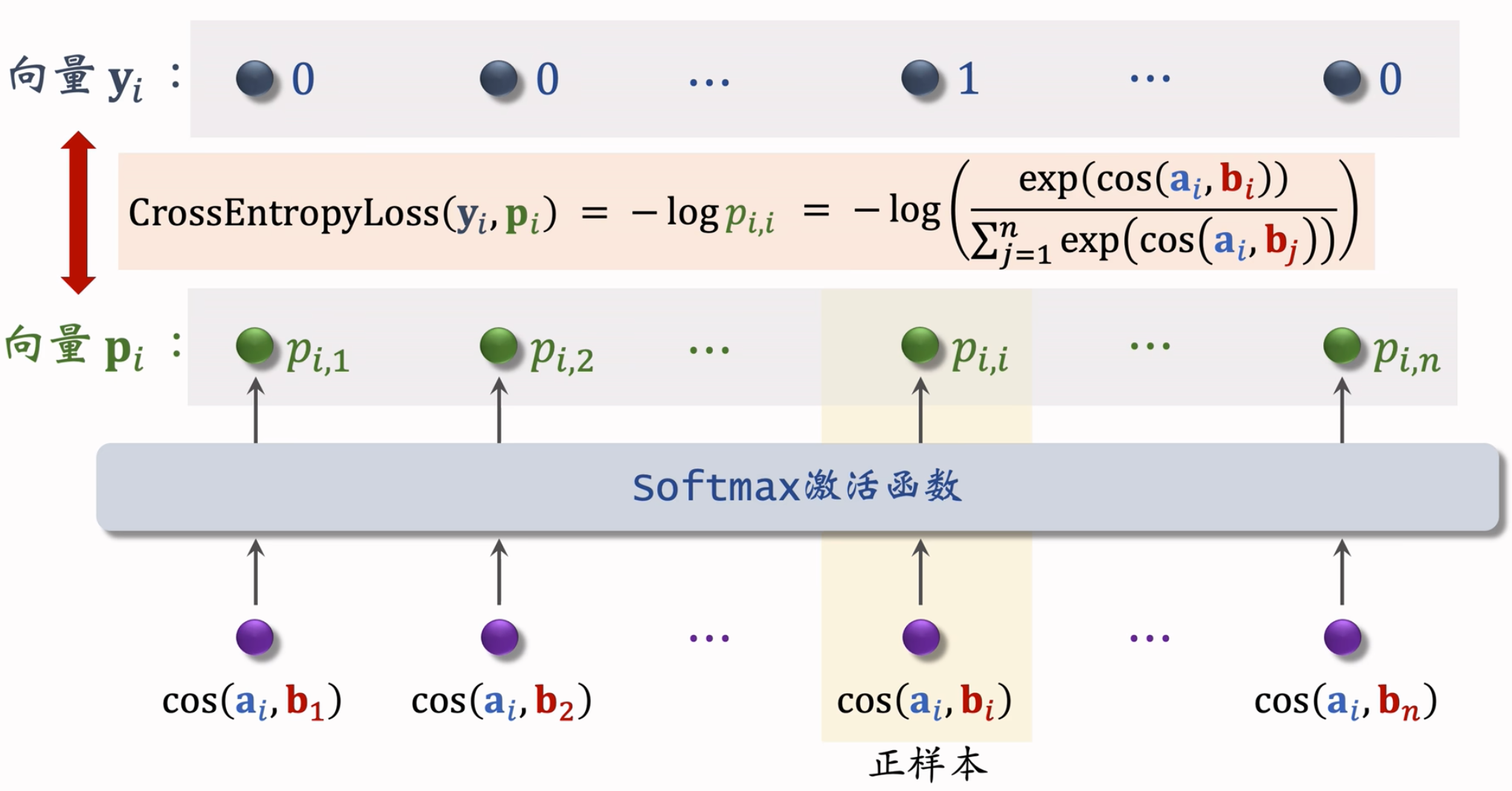
- 双塔损失函数:$L_{main}[i] = -log(\frac{exp(cos(a_i, b_i)-log\ p_i)}{\sum_{j=1}^{n}exp(cos(a_i, b_j))-log\ p_{j}})$,这个地方i为对应的第i个用户。
- 做梯度下降,减少损失函数:$\frac{1}{n}\sum_{i=1}^{n}L_{main}[i]$,这里指的是一个batch中,所有n个用户在双塔函数上的损失的平均值。
同时训练用户塔和物品塔。
Self-supervised Learning
用于训练物品塔。
对于不同的item,分别做多种变换,会得到多个特征,但是从广义上讲,应该满足:
- 同一个物品即使做了不同的变换,在经过物品塔后,也应该拿到相似的Embedding,越相似越好。
- 不同的物品,不管做了什么样的变换,他们的Embedding都不应该相似,越不同越好。
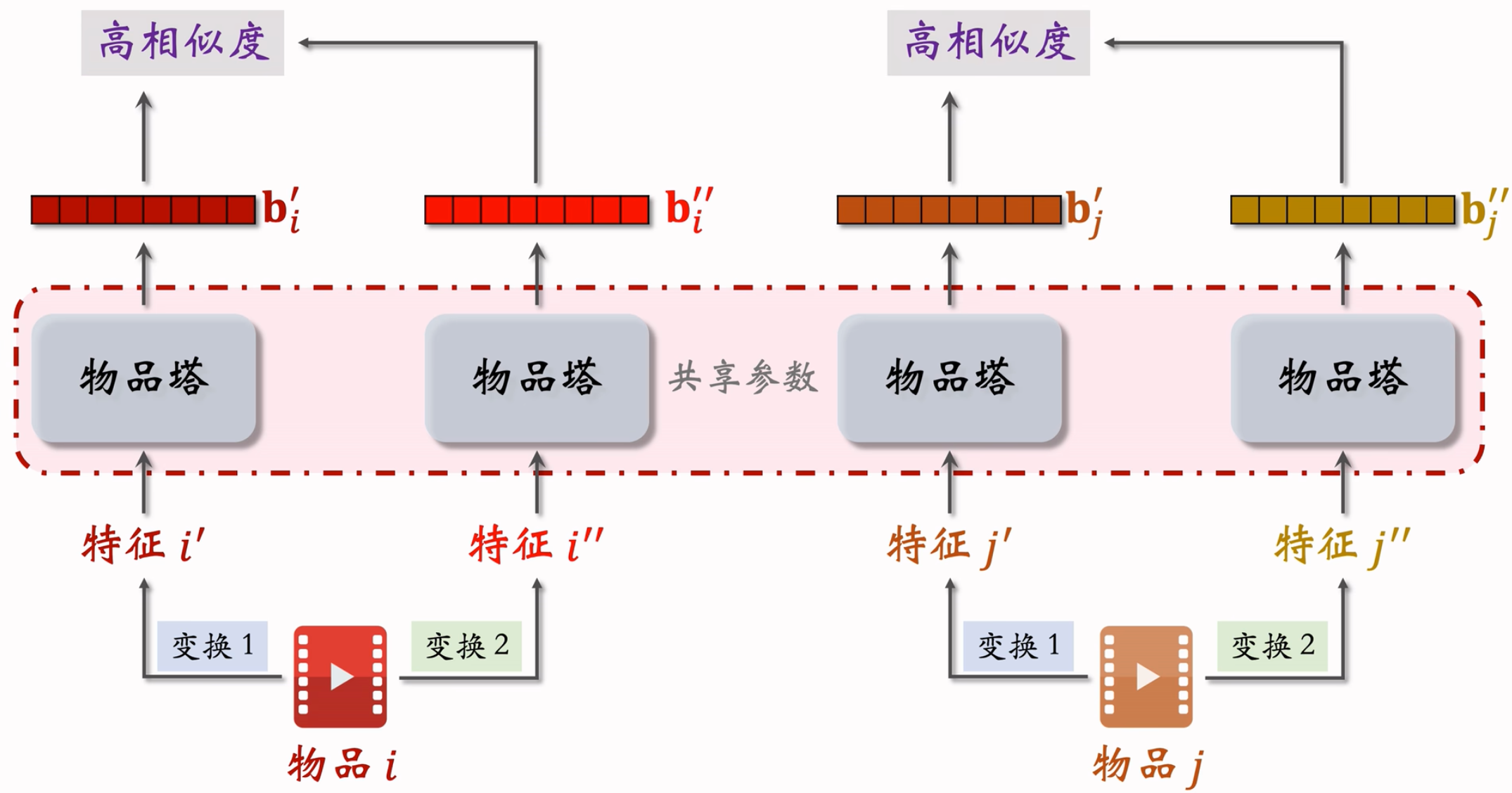
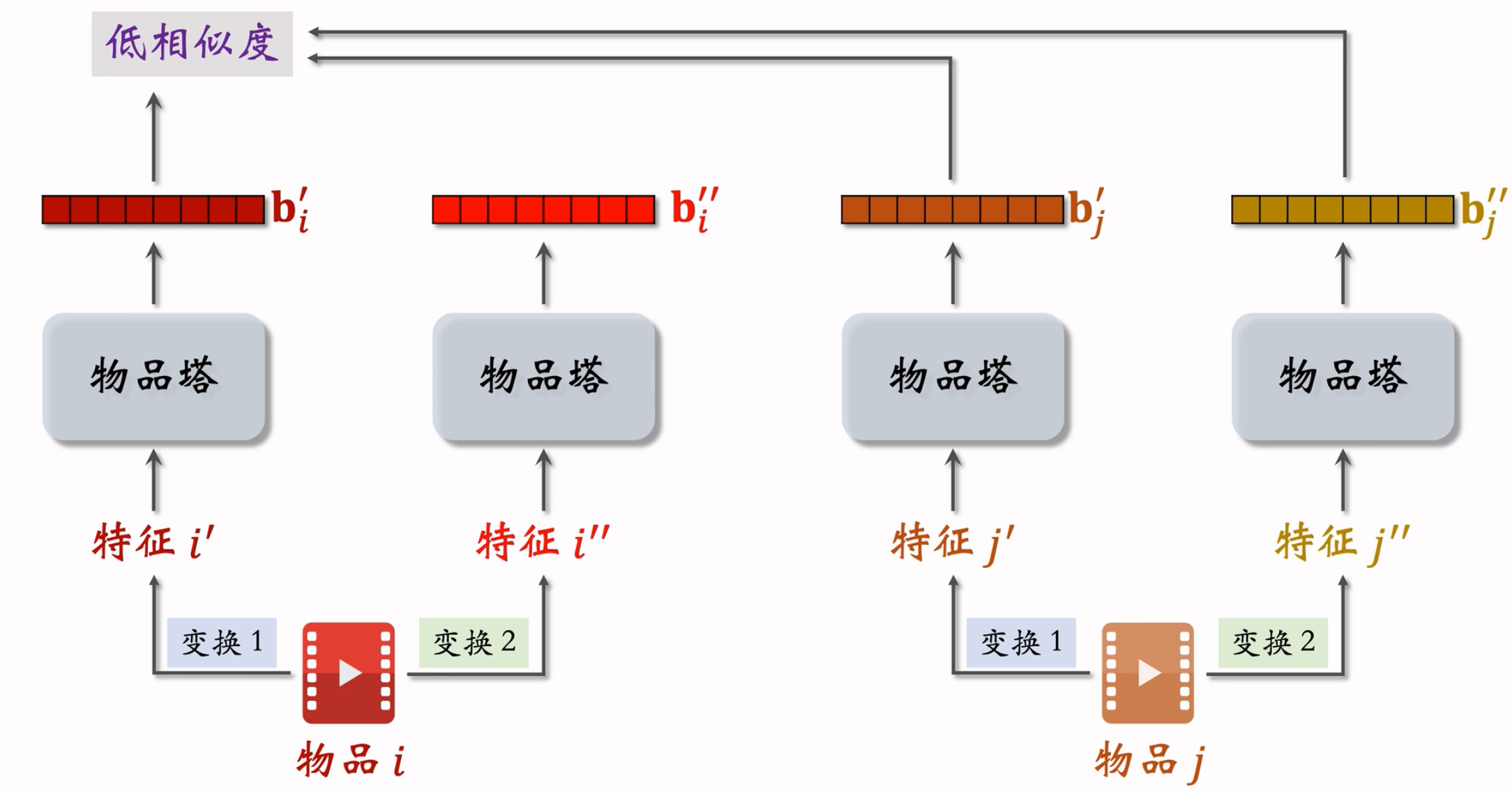
- 物品i的两个向量表征$b_{i}^{‘}$和$b_{i}^{‘’}$有较高的相似度,物品i和j的向量表征$b_j^{‘}$和$b_j^{‘’}$有较低的相似度。鼓励$cos(b_{i}^{‘}, b_{i}^{‘’})$尽量大,$cos(b_{i}^{‘}, b_{j}^{‘’})$尽量小。
自监督学习常用的特征变换
- Random mask
- 随机选一些离散特征(比如类目),把它们遮住。
- 例:某物品的类目特征是U={数码,摄影},之前有可能是分别搞出来embedding,然后加和平均之类的。现在是直接遮住!
- Mask后的类目特征是U’={default},意思是默认的缺失值,然后对于Default做Embedding。相当于物品的类目特征直接整个被“丢掉”了。
- Dropout(仅对多值离散特征生效)
- 一个物品可以有多个类目,那么类目是一个多值离散特征。Dropout:随机丢弃特征中50%的值。
- 例:某物品的类目特征是U={美妆,摄影}。Dropout后的类目特征是U’={美妆}。
- 互补特征(complementary)
- 假设物品一共有4种特征:ID,类目,关键词,城市。正常做法:四个特征的值分别做Embedding,然后拼起来输入物品塔,得到物品的向量表征。
- 随机分成两组:{ID, 关键词}和{类目,城市}。
- {ID,default,关键词,default} -> 物品表征,{default,类目,default,城市} -> 物品表征。由于是同一个物品的表征,鼓励上面两个向量相似,cos大。
- Mask一组关联的特征
- 为啥这么做?特征之间有较强的关联,遮住一个特征并不会损失太多信息。模型可以从其他强关联特征中,学到遮住的特征。最好是把关联特征一次全都遮住。
- e.g.
- 受众性别:U={男,女,中性},类目:V={美妆,数码,足球,摄影,科技,…}
- u=女 和 v=美妆 同时出现的概率 p(u,v) 大,u=女 和 v=数码 同时出现的概率p(u,v)小。这里性别和类目的关联就很强。
- p(u):某特征取值为u的概率。p(男性)=20%,p(女性)=30%。p(中性)=50%
- p(u,v):某特征取值为u, 另一个特征取值为v, 同时发生的概率。p(女性,美妆)=3%,p(女性,数码)=0.1%
- 离线计算特征两两之间的关联,用互信息(mutual
information)衡量:$MI(\mathcal{U}, \mathcal{V}) = \sum_{u\in\mathcal{U}}\sum_{v\in\mathcal{V}}p(u,v)\times log\frac{p(u,v)}{p(u).p(v)}$,两种特征关联强,p(u, v)就比较大,MI就会大。
- 设一共有k种特征。离线计算特征两两之间MI,得到k x k的矩阵。随机选一个特征作为种子,找到种子最相关的k/2种特征。Mαsk种子及其相关的k/2种特征,保留其余的k/2种特征。
- 优缺点:
- 好处:比random mask、dropout、互补特征等方法
效果更好。 - 坏处:方法复杂,实现的难度大,不容易维护。每添加一个新的特征,都要重新算一遍所有特征的MI。对于业界来讲,ROI太低了!
- 好处:比random mask、dropout、互补特征等方法
- Random mask
训练模型:
从全体物品中均匀抽样,得到m个物品作为一个batch。
做两类特征变换,物品塔输出两组向量:b1’, b2’, …, bm’和b1’’, b2’’, …, bm’’。
第i个item的损失函数:$L_{self}[i] = -log(\frac{exp(cos(b_i^{‘}, b_i^{‘’}))}{\sum_{j=1}^{m}exp(cos(b_i^{‘}, b_j^{‘’}))})$
示意图:
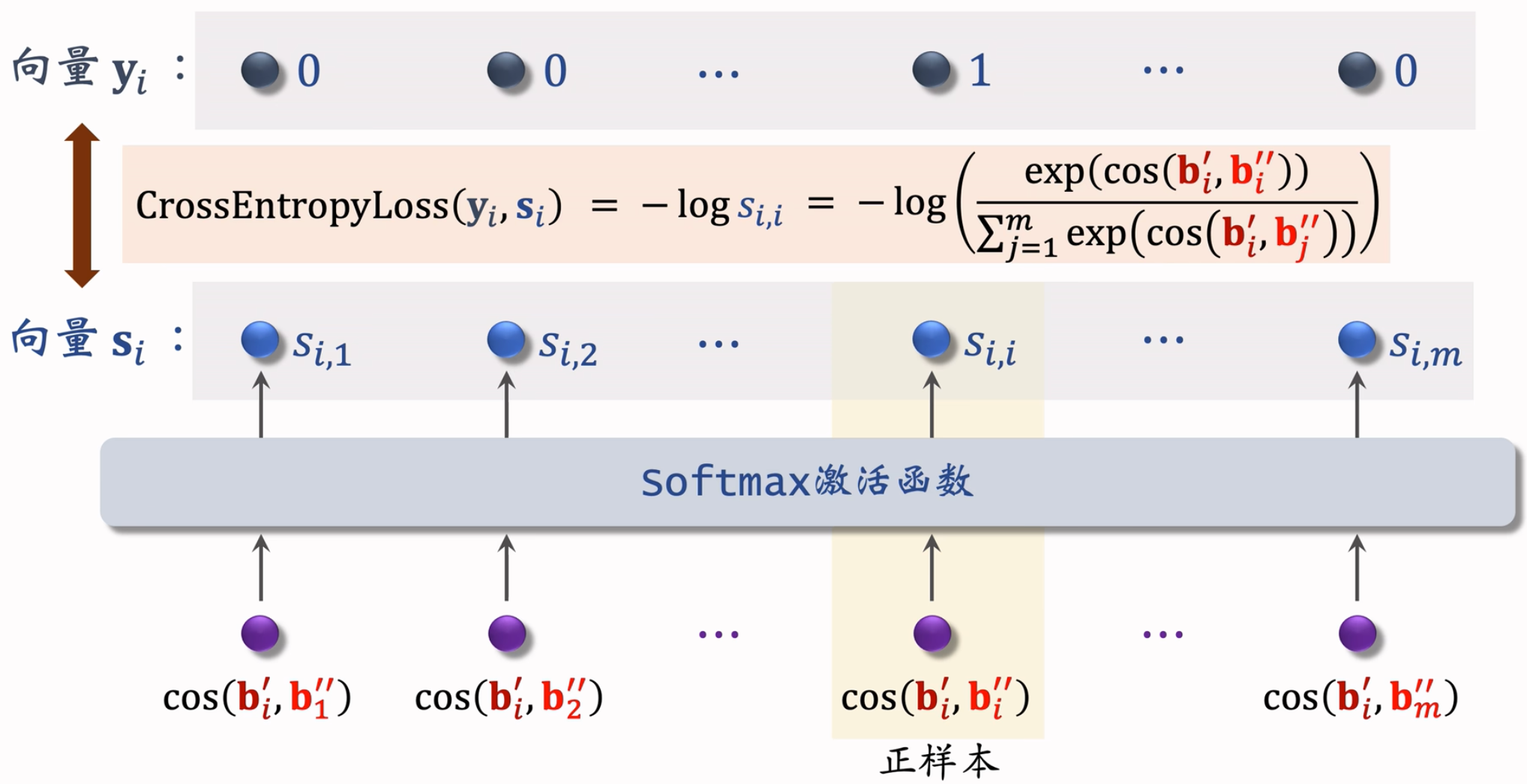
做梯度下降,减少自监督学习的损失:$\frac{1}{m}\sum_{i=1}^{m}L_{self}[i]$,算一个Batch数据Loss的平均值。
Summary
双塔模型学不好低曝光物品的向量表征。
自监督学习
- 对物品做随机特征变换。
- 相同物品的特征向量相似度高,不同物品的特征向量相似度低。
- 实验效果:低曝光物品、新物品的推荐变得更准。
训练模型:
对点击做随机抽样,得到n对用户一物品二元组,作为batch
从全体物品中均匀抽样,得到m个物品作为一个batch
做梯度下降,使得损失减小:$\frac{1}{n}\sum_{i=1}^{n}L_{main}[i] + \alpha.\frac{1}{m}\sum_{j=1}^{m}L_{self}[j]$
前半部分是双塔模型的损失,后半部分是自监督学习的损失。中间的$\alpha$是超参数,决定了自监督学习的作用。
Deep Retrieval
- 经典的双塔模型把用户、物品表示为向量,线上做最近邻查找。Deep Retrieval 把物品表征为路径(path),线上查找用户最匹配的路径。Deep Retrieval类似于阿里的TDM。
- Outline
- 索引:
- 路径 → List<物品>
- 物品 → List<路径>
- 预估模型:神经网络预估用户对路径的兴趣
- 线上召回:用户→路径→物品。
- 训练:
- 学习神经网络参数。
- 学习物品表征(物品 -> 路径)。
- 索引:
Concept
- 物品可以用路径来表示:
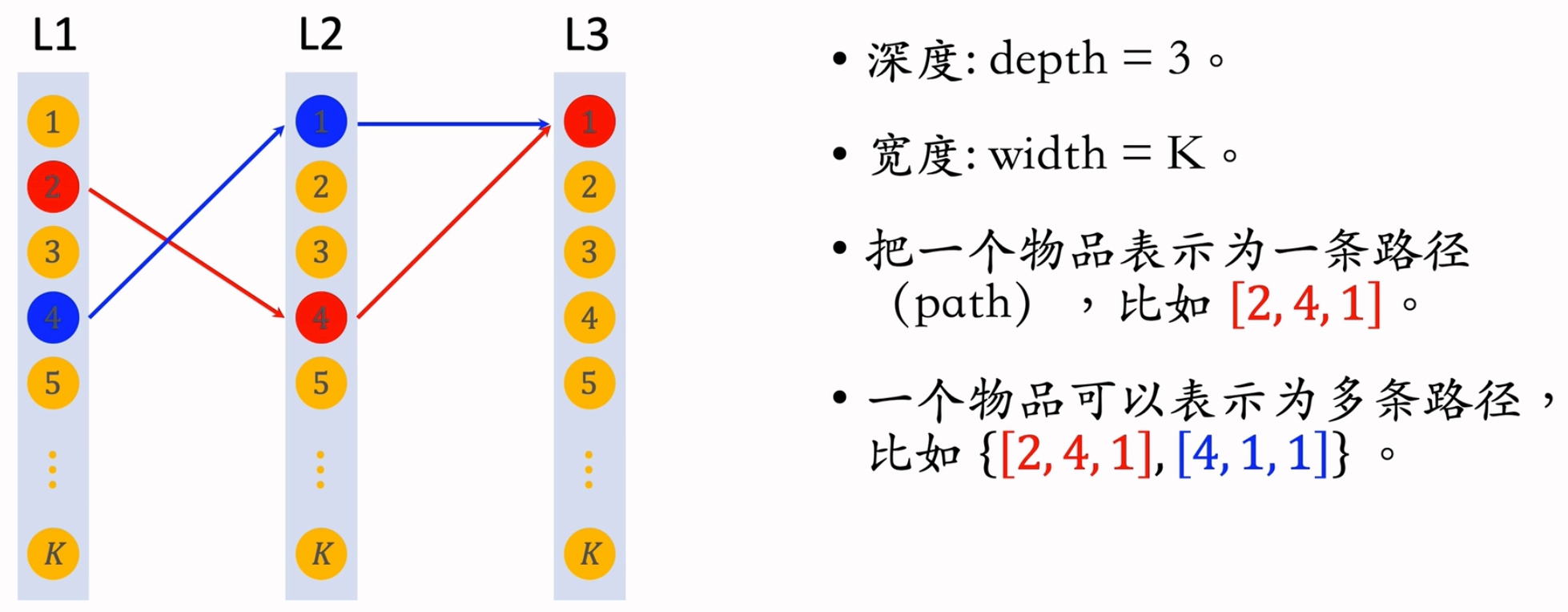
索引:
- item -> List
- 训练的时候使用。
- 一个物品多条路径
- 用三个节点表示一条路径:path = [a, b, c]
- path -> List
- 线上召回的时候使用。
- 一条路径对应多个物品
- item -> List
Deep Retrieval原理
本质是一种神经网络,预估模型,预估用户对路径的兴趣分数。可以根据用户特征召回多条路径。
预估用户对路径的兴趣
条件概率,朴素贝叶斯,用户喜欢a -> 用户喜欢a的情况下喜欢a,b -> 用户喜欢a,b的情况下喜欢a,b,c
算法流程:
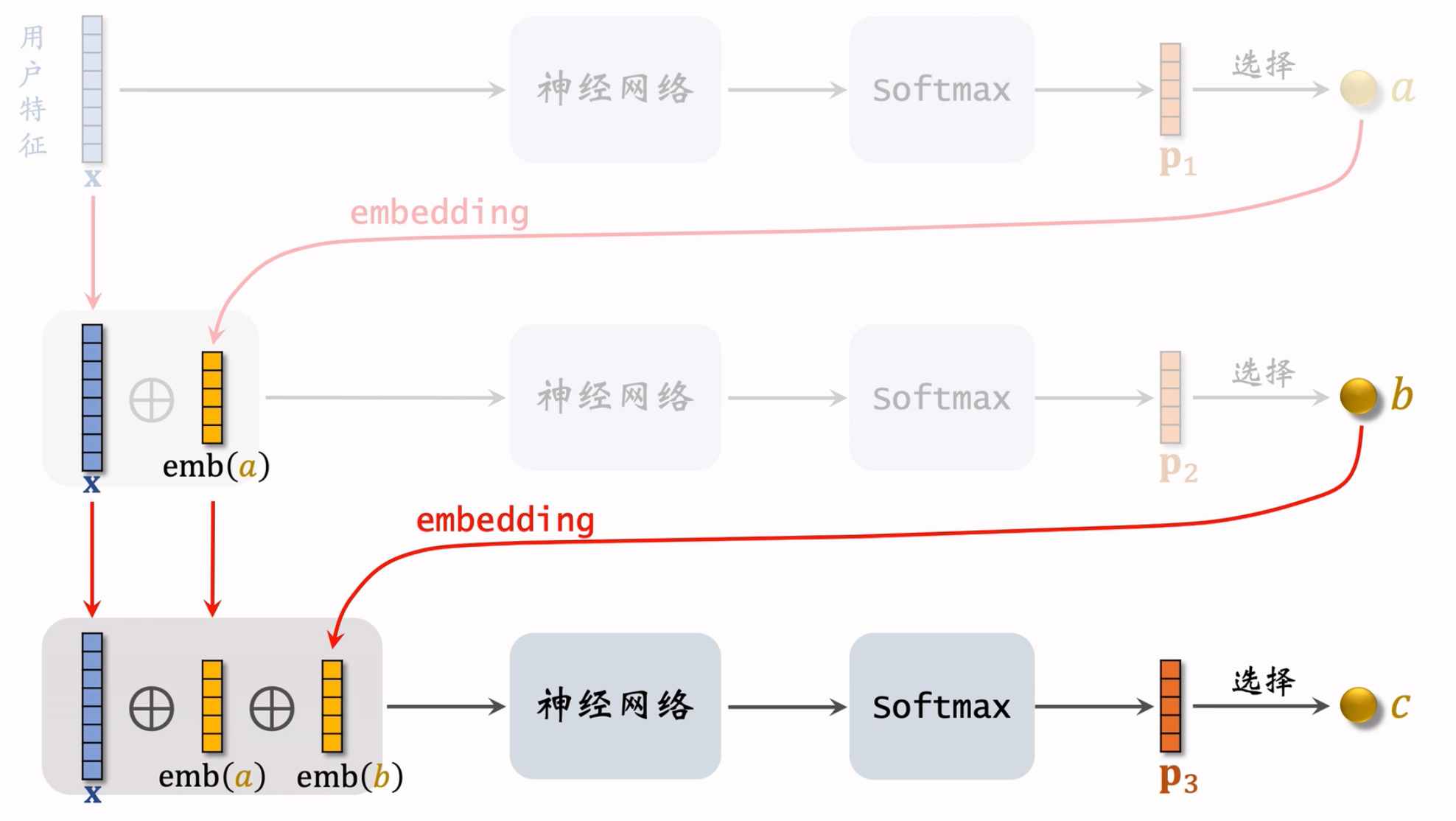
这里的每一层神经网络,都不共享参数的哈!论文中使用的是beam search。
线上召回:
用户 -> 路径 -> 物品,流程
- 第一步:给定用户特征,用beam search召回一批路径。
- 第二步:利用索“path→List(item)”, 召回一批物品,每条路径对应多个物品。
- 第三步:对物品做打分和排序,选出一个子集。打分没有限制,小的排序模型就行,例如双塔模型。
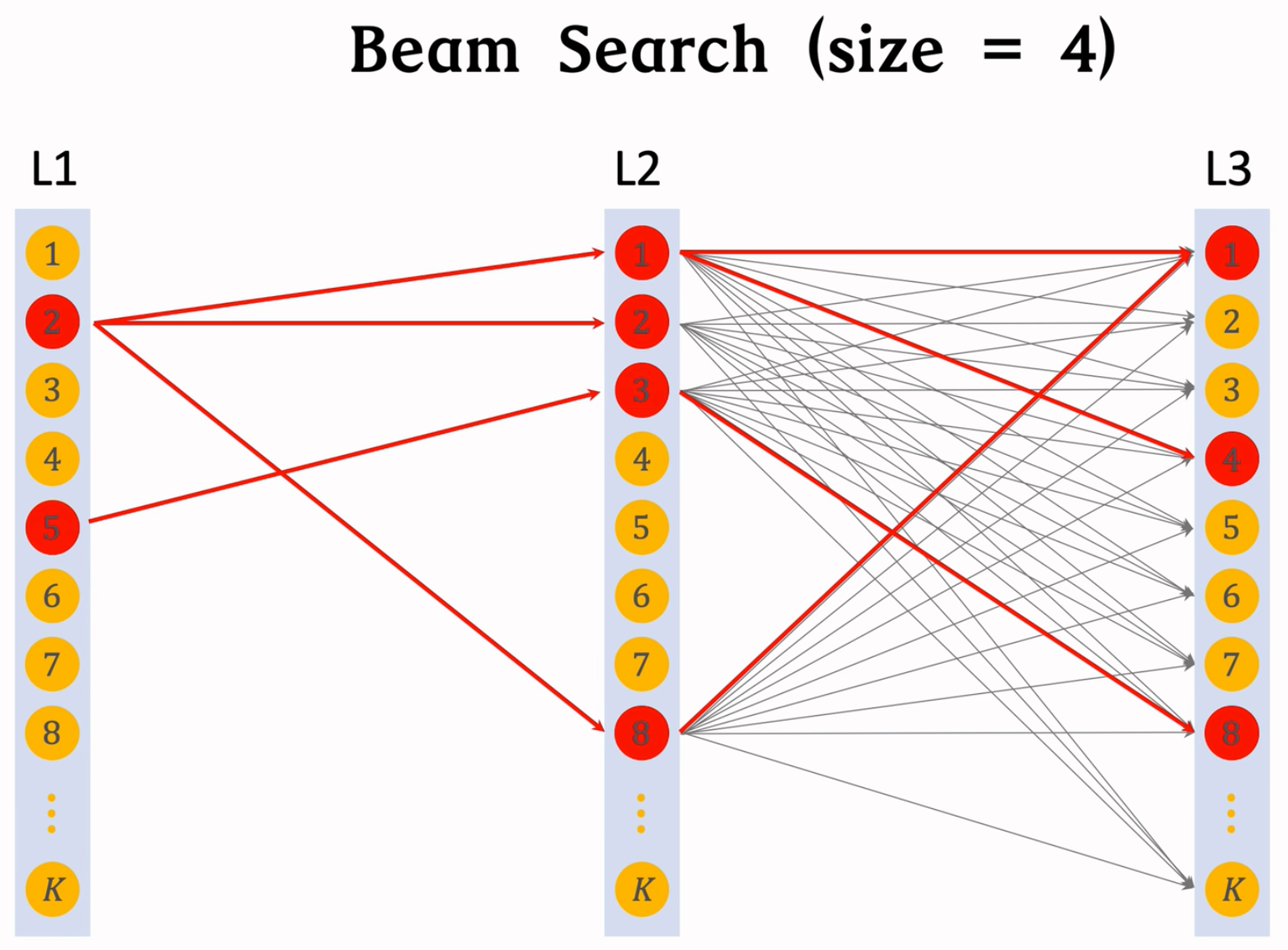
Beam Search
假设有3层,每层K个节点,那么一共有K^3条路径。用神经网络给所有K3条路径打分,计算量太大。
用beam search,可以减小计算量。需要设置超参数beam size。Beam_size = 1就是贪心,越大,全局效果越好!一个Demo:
训练:
同时学习神经网络参数和物品表征。
- 神经网络p(a,b,c | x)预估用户对路径[a,b,c]的兴趣
- 把一个物品表征为多条路径{[a,b,c]},建立索引
- item -> List(path),
- path -> List(item)。
训练只用正样本(user, item): click(user, item) = 1,用户点过就算正样本。
神经网络参数:
- 这个神经网络用来表征用户对于物品多感兴趣,物品表征为J条路径:[a1, b1, c1], …, [aj, bj, cj]
- 用户对路径a, b, c感兴趣。如果用户点击过物品,说明用户对这个物品的所有J条路径感兴趣,这时候就应该让$\sum_{j=1}^{J}p(a_j, b_j, c_j\ | \ x)$变大。
- 损失函数:$loss = -log(\sum_{j=1}^{J}p(a_j, b_j, c_j\ | \ x))$
学习物品表征:
用户user对路径path=[a,b,c]的兴趣记作 $p(path | user)=p(a,b,c | x)$.
item与path的相关性:$score(item, path) = \sum_{user}p(path|user)\times click(user, item)$,第一项是用户对于路径的兴趣,神经网络预估,click点击了就是1,没点击就是0。
根据Score选出J条路径,作为item的表征。
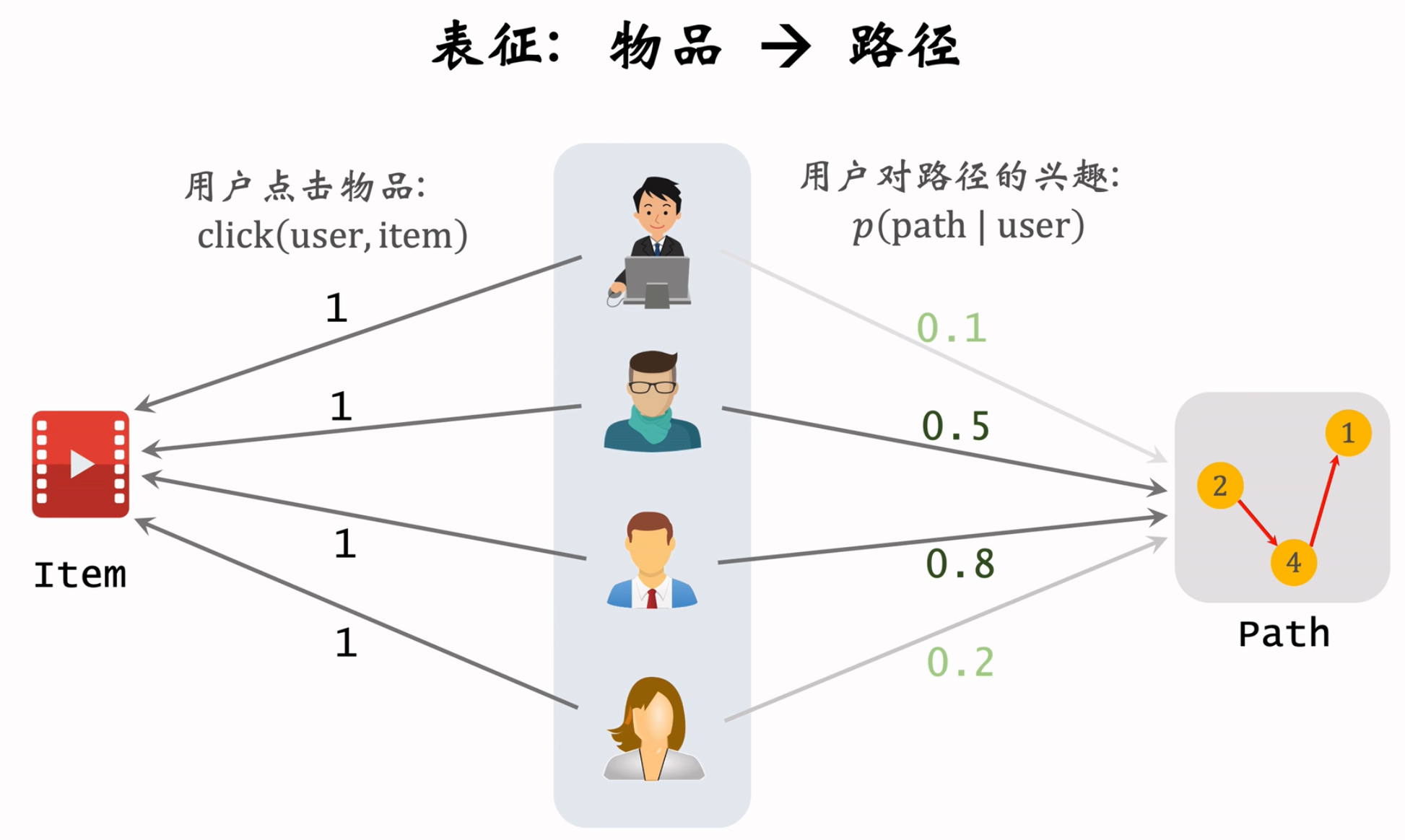
通过用户为“中介”,串联路径和物品的关系。
选出J条路径$\pi = {path1,…,path}$,作为物品的表征。
损失函数(选择与item高度相关的path):
$loss(item,\pi)=-log(\sum_{j=1}^{J}score(item,path_{j}))$正则项(避免过多的item集中在一条path上):
$reg(path_j)=(number\ of\ items\ on\ path )^4$贪心算法更新路径:每次固定j-1条路径,并从从来没有被选中的路径中,选出一条新作为新的path,$argmin_{path_l}loss(item, \pi) + \alpha\times{reg(path_l)}$
较高的分数score,而且路径上的物品不会太多。
Summary
更新神经网络
- 神经网络判断用户对路径的兴趣
$p(path \ | \ x)$. - 训练所需的数据
- “物品→路径”的索引
- 用户点击过的物品。
- 如果用户点击过物品,且物品对应路径path,则更新神经网络参
数使$p(path|x)$变大
- 神经网络判断用户对路径的兴趣
更新物品表征
- 判断物品与路径的相关性:
- 物品 ← 用户 → 路径
- 用户点击过物品(物品 ← 用户)
- 神经网络的打分(用户 → 路径)
- 让每个物品关联J条路径
- 物品和路径要有很高的相关性。
- 一条路径上不能有过多的物品。
- 判断物品与路径的相关性:
在线召回:用户 -> 路径 -> 物品
- 根据神经网络,给定用户的特征,可以算出对于路径的感兴趣程度。
- Beam search召回最高的 s 条路径。
- 根据上面物品表征过程中建立的索引,根据路径,查找到路径上的n个物品。
- 一共召回 s x n 个物品,排序,返回分数高的若干物品。
Deep Retrieval本质:路径作为用户和物品的中介。双塔本质:用向量表征作为用户和物品的中介。
- 离线训练
- 同时学习 用户—路径,物品—路径的关系。
- 用户—路径:
- 一个物品被表征为J条路径,存储在物品 -> 路径的索引上。(现有数据:物品 -> 路径)
- 如果用户点击过物品,则更新神经网路参数,分数变大。(现有数据:用户 -> 物品)
- 可以训练模型,学习:用户 -> 路径的兴趣,使得用户对于感兴趣的物品,对应的路径的加和增大。
- 物品—路径:
- 上面神经网络线训出来了,这个时候就可以用来判断,任意的用户对于任意的路径的感兴趣程度。(现有数据:用户 -> 路径)
- 如果用户还点击过物品。(现有数据:用户 -> 物品)
- 可以学习到:路径和物品的关系,感兴趣的path和实际点击过的物品,这两者关联性高。
- 寻找与Item相关的 J 条路径,且避免一条路径上的物品过多。
Other recall channels
GeoHash
GeoHash 召回
用户可能对附近发生的事感兴趣
GeoHash:对经纬度的编码,大致表示地图上一个长方形区域
索引:GeoHash → 优质笔记列表(按时间倒排)
这条召回通道没有个性化(正因为如此,才需要有优质笔记列表)
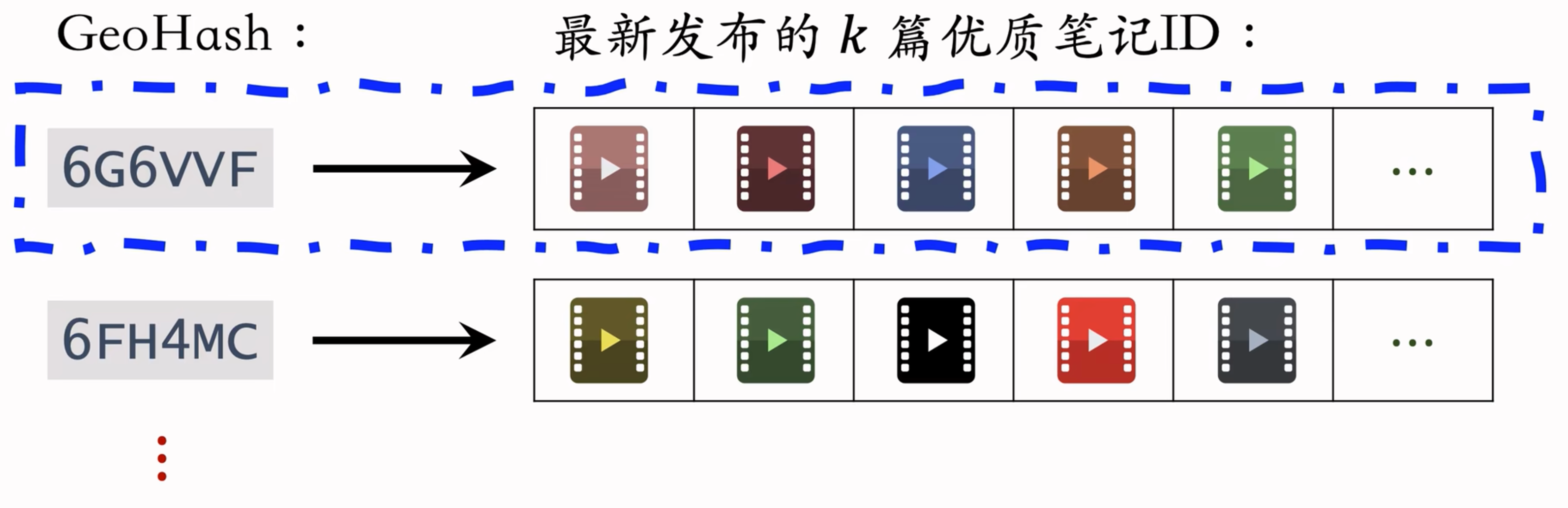
根据用户定位的 GeoHash,取回该地点最新的 $k$ 篇优质笔记
同城召回
- 用户可能对同城发生的事感兴趣
- 索引: 城市 → 优质笔记列表(按时间倒排)
- 这条召回通道没有个性化
Author
- 作者召回
- 关注作者召回
- 用户对关注的作者发布的笔记感兴趣。索引:
- 用户 → 关注的作者
- 作者 → 发布的笔记
- 召回: 用户 → 关注的作者 → 最新的笔记
- 用户对关注的作者发布的笔记感兴趣。索引:
- 有交互的作者召回
- 如果用户对某笔记感兴趣(点赞、收藏、转发),那么用户可能对该作者的其他笔记感兴趣
- 索引: 用户 → 有交互的作者,作者列表需要定期更新,加入最新交互的作者,删除长期未交互的作者
- 召回: 用户 → 有交互的作者 → 最新的笔记
- 相似作者召回
- 如果用户喜欢某作者,那么用户喜欢相似的作者
- 索引:作者 → 相似作者($k$ 个作者)
- 作者相似度的计算类似于 ItemCF 中判断两个物品的相似度
- 例如两个作者的粉丝有很大重合,则认定两个作者相似
- 召回:用户 → 感兴趣的作者 → 相似作者 → 最新的笔记
($n$ 个作者) ($nk$ 个作者)($nk$ 篇笔记)
- 关注作者召回
Cache
- 缓存召回
- 想法:复用前 $n$ 次推荐精排的结果
- 背景:
- 精排输出几百篇笔记,送入重排
- 重排做多样性抽样,选出几十篇
- 精排结果一大半没有曝光,被浪费
- 精排前 50,都是用户非常感兴趣的,但是没有曝光而已,值得再次尝试。缓存起来,作为一条召回通道。
- 缓存大小固定,需要退场机制
- 一旦笔记成功曝光,就从缓存退场
- 如果超出缓存大小,就移除最先进入缓存的笔记
- 笔记最多被召回 10 次,达到 10 次就退场
- 每篇笔记最多保存 3 天,达到 3 天就退场
- 上面这里介绍的规则都比较简单粗暴,还能够有更多的策略,再来细化规则。
Exposure filter & Bloom filter
曝光过滤问题:
如果用户看过某个物品,则不再把该物品曝光给该用户。
对于每个用户,记录已经曝光给他的物品。(小红书只召回1个月以内的笔记,因此只需要记录每个用户最近1个月的曝光历史。)
对于每个召回的物品,判断它是否已经给该用户曝光过,排除掉曾经曝光过的物品。
一位用户看过几个物品,本次召回r个物品,如果暴力对比,需要O(nr)的时间。
小红书为例子,用户一个月n的量级在几千,每次召回r的量级也在几千。如果nr的话,暴力对比的计算量太大了。
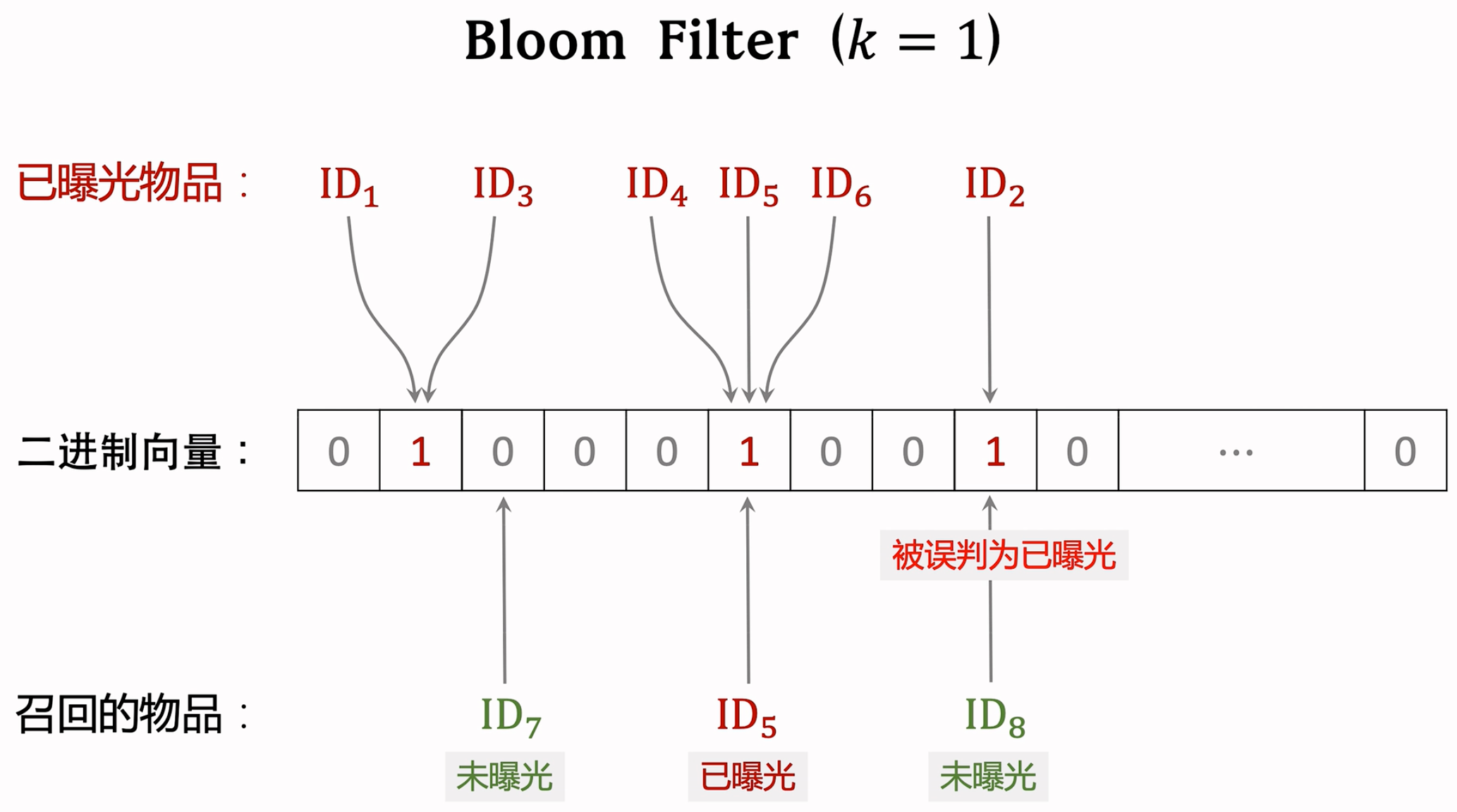
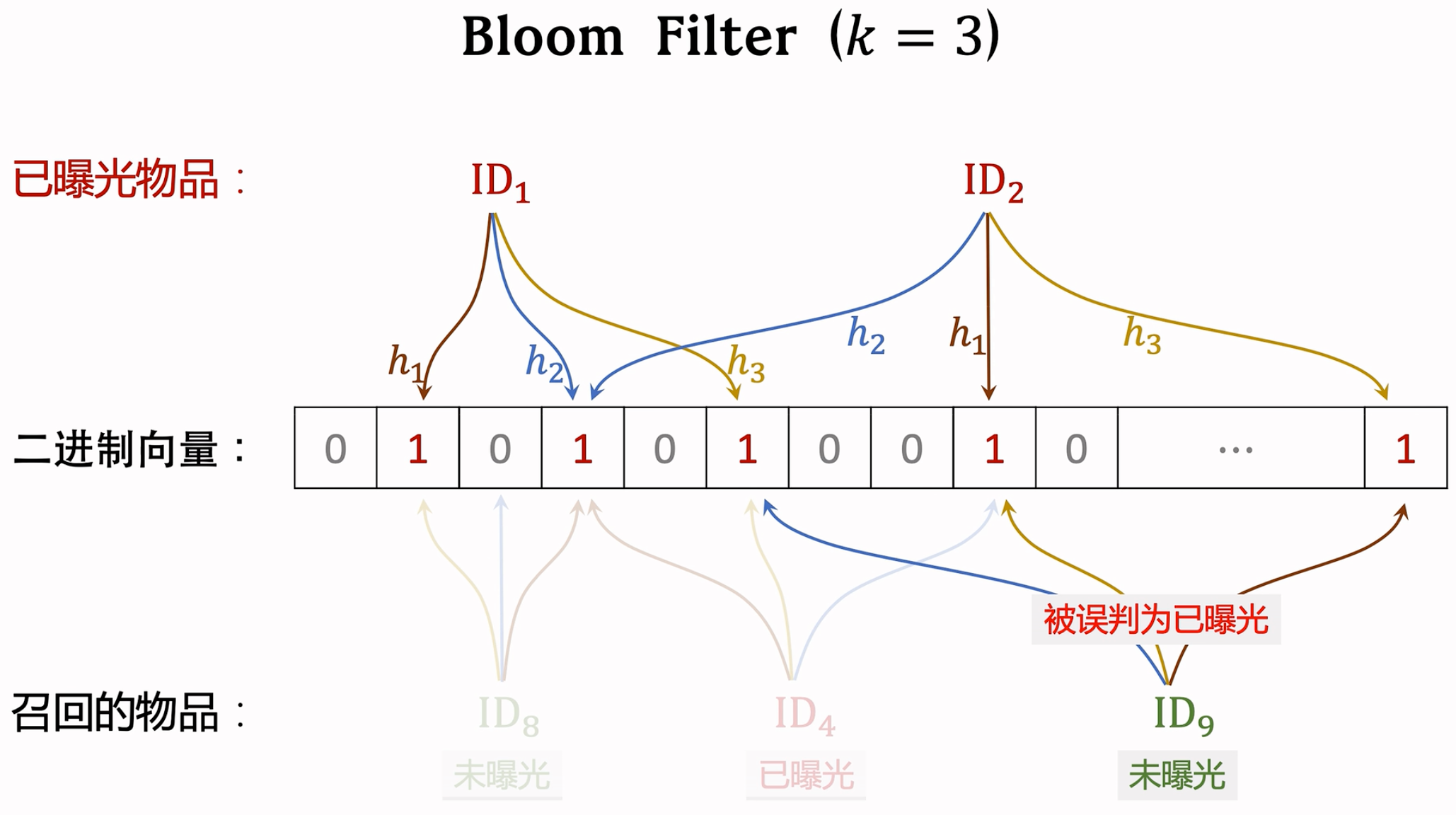
Bloom Filter:
Bloom filter判断一个物品ID是否在已曝光的物品集合中。
如果判断为no,那么该物品一定不在集合中。
如果判断为yes,那么该物品很可能在集合中。(可能误伤,错误判断未曝光物品为已曝光,将其过滤掉。)
Bloom filter把物品集合表征为一个m维二进制向量。每个用户有一个曝光物品的集合,表征为一个向量,需要m bit的存储。Bloom filter有k个哈希函数,每个哈希函数把物品D映射成介于 0 和 m-1 之间的整数。
Demo
曝光过滤的链路:
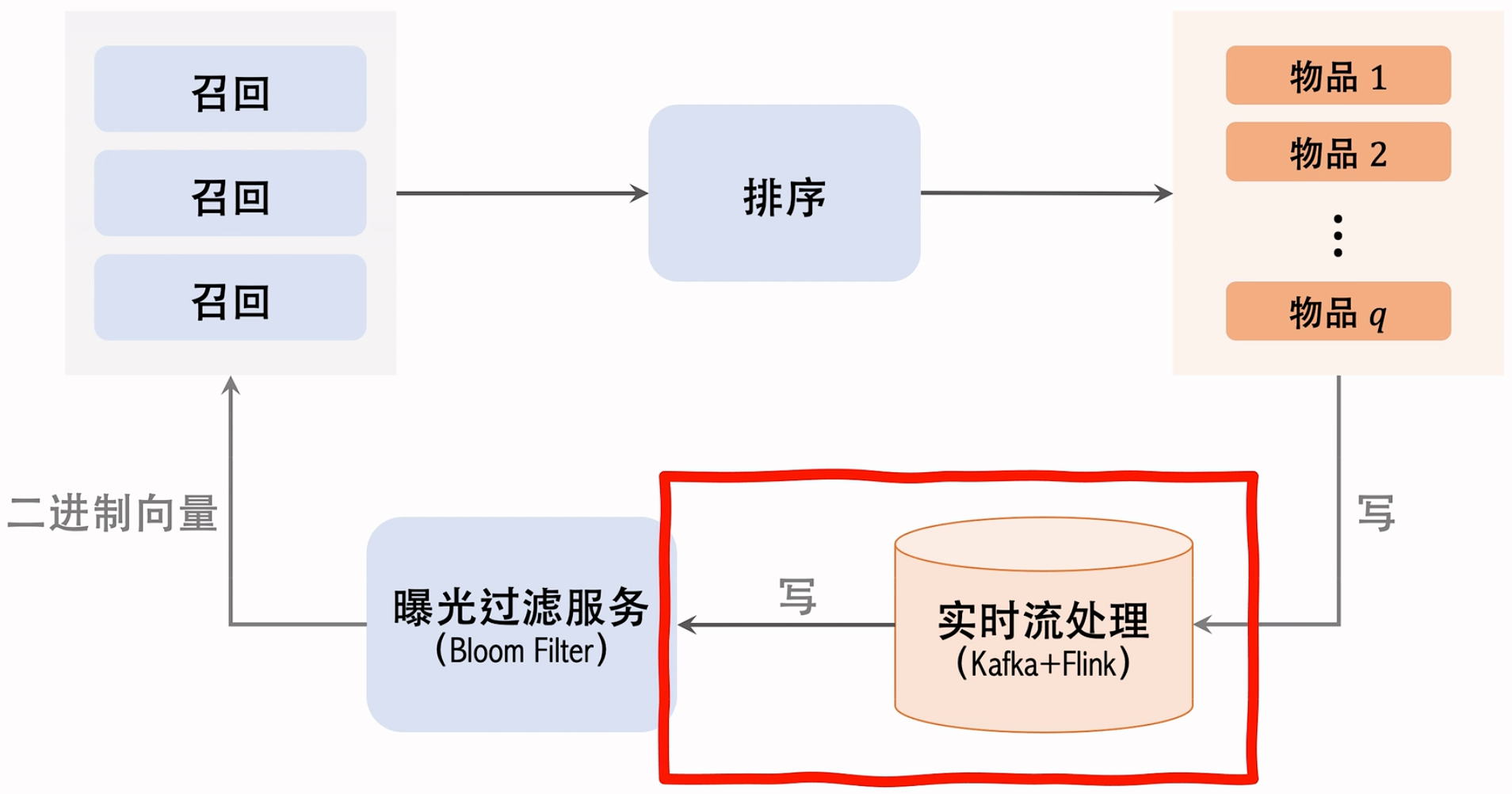
实时流处理要足够快哈,不然用户刷着刷着,很容易就出现重复了。这一块儿挂了/延时特别大,其实也是比较常见的情况。
缺点
- Bloom filter只支持添加物品,不支持删除物品。从集合中移除物品,无法消除它对向量的影响。
- 每天都需要从物品集合中移除年龄大于1个月的物品(超龄物品不可能被召回,没必要把它们记录在Bloom filter,降低n可以降低误伤率。),这种场景Bloom Filter用起来就有点困难。
Sort
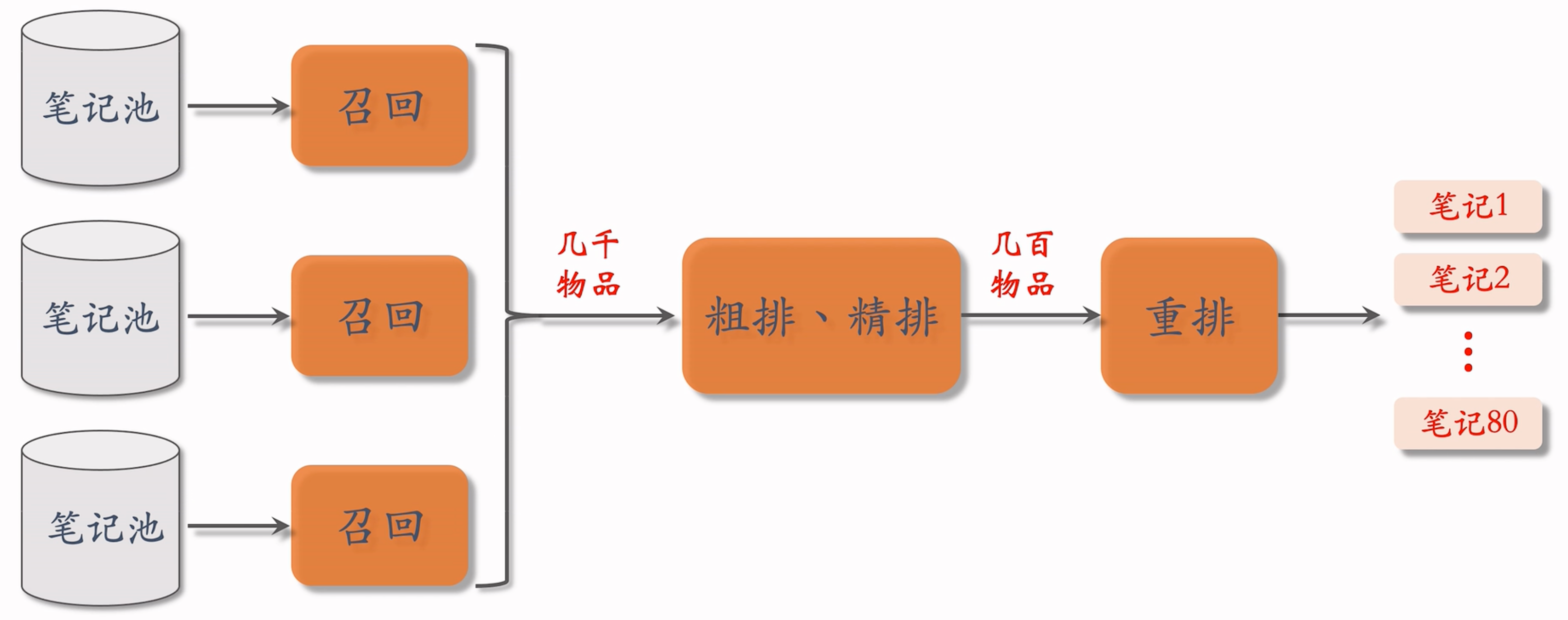
- 本节内容集中在粗排和精排,它们的原理基本相同,只是粗排模型小,用的特征少,效果差一些。
- 粗排的目的是做快速的初步筛选,如果不用粗排,直接对于几千篇笔记用很大的精排模型,计算代价承受不住。(这里还有一致性的问题,参考这篇博客)。
- 流程
- 召回:很多召回通道,从几亿 -> 几千。
- 粗排给笔记打分,几千 -> 几百。精排对于选出的几百篇笔记打分,不做截断,让几百篇笔记带着精排的分数直接进入重排。
- 重排做多样性抽样,并且打散相似内容。最终只有几十篇笔记被选中,展示给用户。
Multi-objective ranking model
用户—笔记的交互:
- 排序的主要依据是用户对笔记的兴趣,而兴趣都反映在 用户—笔记 的交互中。
- 对于每篇笔记,系统记录:
- 曝光次数(number of impressions)
- 点击次数(number of clicks)
- 点赞次数(number of likes)
- 收藏次数(number of collects)
- 转发次数(number of shares)
- 点击率 = 点击次数 / 曝光次数
- 点赞率 = 点赞次数 / 点击次数
- 收藏率 = 收藏次数 / 点击次数
- 转发率 = 转发次数 / 点击次数 (少见行为,远少于上面的点赞和收藏,转发到外部平台可以引流!)
- 排序的依据
- 排序模型预估点击率、点赞率、收藏率、转发率等多种分数
- 融合这些预估分数(比如加权和)
- 根据融合的分数做排序、截断。保留分数高的笔记,淘汰分数低的笔记。
- 对于每篇笔记,系统记录:
- 排序的主要依据是用户对笔记的兴趣,而兴趣都反映在 用户—笔记 的交互中。
多目标模型:
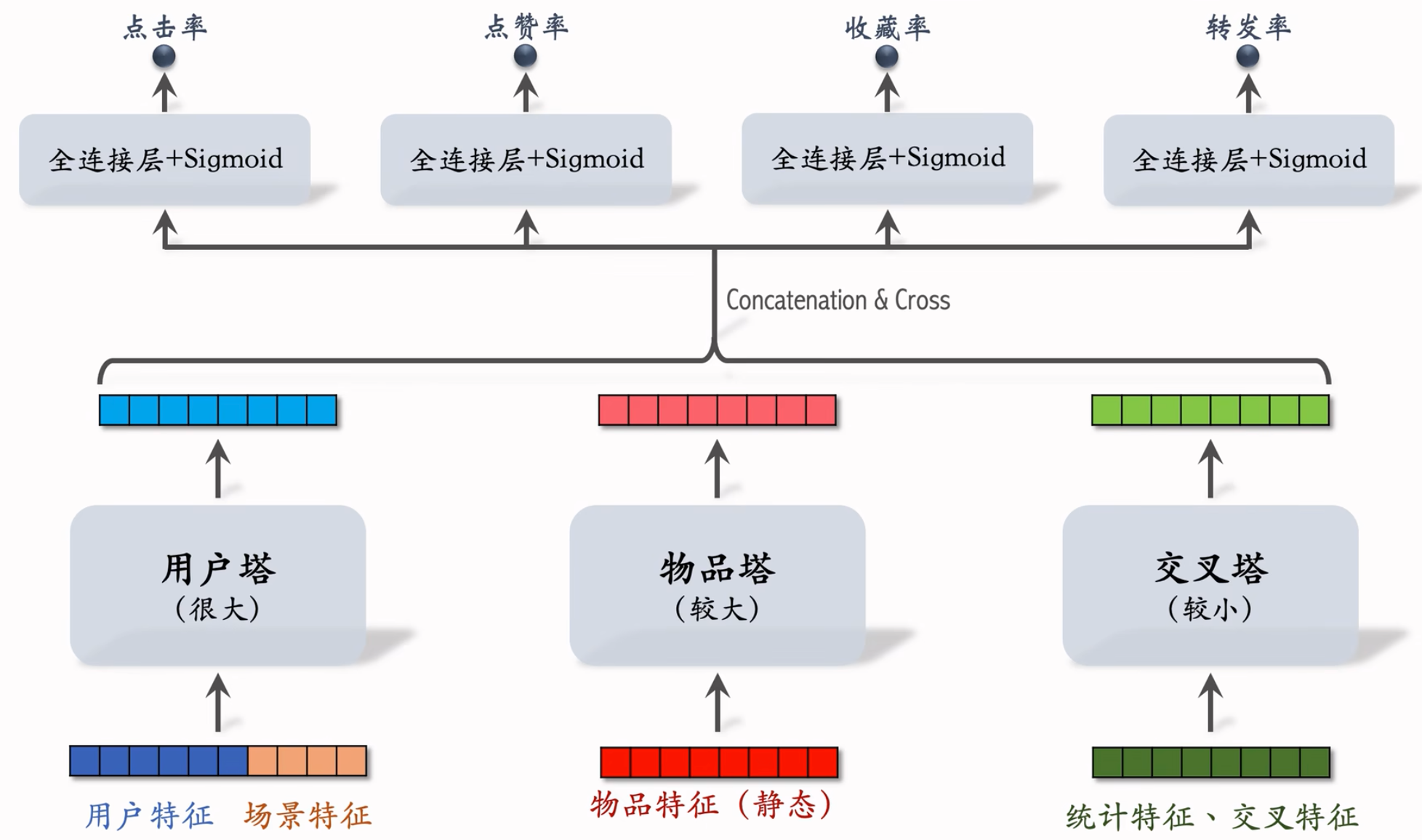
模型结构:
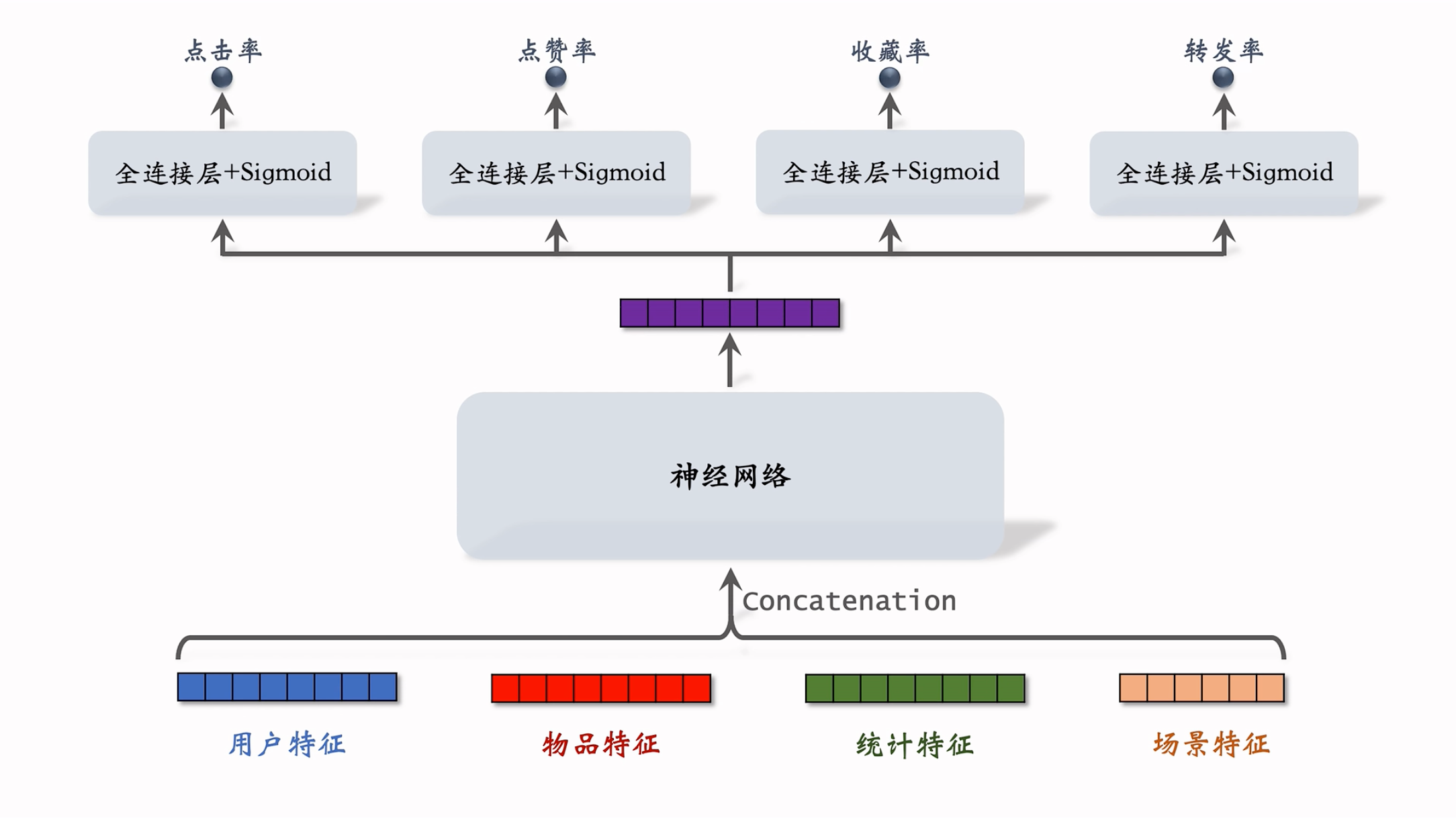
统计特征包括”用户统计特征”和”物品统计特征”,”场景特征” 是随着用户请求传过来的。
损失函数:

实际数据其实是0/1(二元分类),用户是否点击/点赞这样的指标,然后和我们神经网路输出的possibility做比较,得到损失,
训练:让预估值接近真实目标值
- 总的损失函数: $\sum^4_{i=1}{α_i·\rm{CrossEntropy}(y_i,p_i)}$
- 对损失函数求梯度,做梯度下降更新参数
- 困难:类别不平衡,即正样本数量显著少于负样本
- 每 100 次曝光,约有 10 次点击、90 次无点击
- 每 100 次点击,约有 10 次收藏、90 次无收藏
- 不平衡的影响在于:太多负样本用处不大,白白浪费计算资源。
- 解决方案:负样本降采样(down-sampling)
- 保留一小部分负样本
- 让正负样本数量平衡,节约计算量。
预估值校准
- 做了降采样后训练出的预估点击率会大于真实点击率。
- 正样本、负样本数量为 $n_+$ 和 $n_-$,对负样本做降采样,抛弃一部分负样本 。
- 使用 $\alpha . n_-$ 个负样本,$\alpha$是采样率,在[0, 1] 之间。由于负样本变少,预估点击率大于真实点击率。 采样的负样本越少,对于点击率的高估越大。
- 校准公式:
- 真实点击率:$p_{true} = \frac{n_+}{n_- +n_+}$
- 预估点击率:$p_{pred} = \frac{n_+}{n_+ +\alpha . n_-}$
- 可以得到校准公式,从pred -> true: $p_{true} = \frac{\alpha.p_{pred}}{(1-p_{pred}) + \alpha.p_{pred}}$
参考文献:1. Xinran He et al. Practical lessons from predicting clicks on ads at Facebook. In the 8th International Workshop on Data Mining for Online Advertising.
Multi-gate Mixture-of-Experts(MMoE)
模型结构:
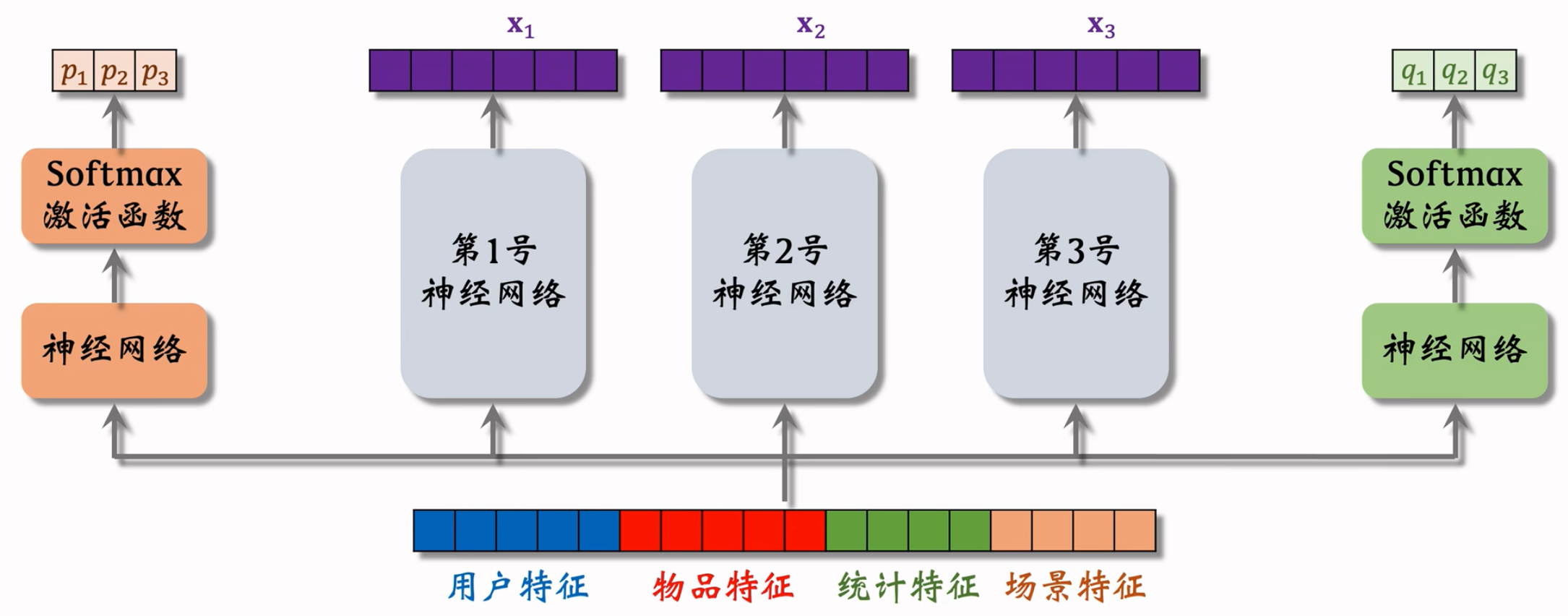
三个神经网络结构相同,但是不共享参数。专家神经网络的数量是超参数,实践中通常用 4 个或 8 个。
把特征向量输入左侧的神经网络,再通过 Softmax 输出 $p_1,p_2,p_3$ 分别对应 3 个专家神经网络。用 $p_1,p_2,p_3$ 作为权重,对 3 个专家神经网络的输出 $x_1,x_2,x_3$ 进行加权平均。
采取同样方法,将特征向量输入右侧的神经网络,得到的 $q_1,q_2,q_3$ 可以与专家神经网络的输出组成另一个预估值的输入。
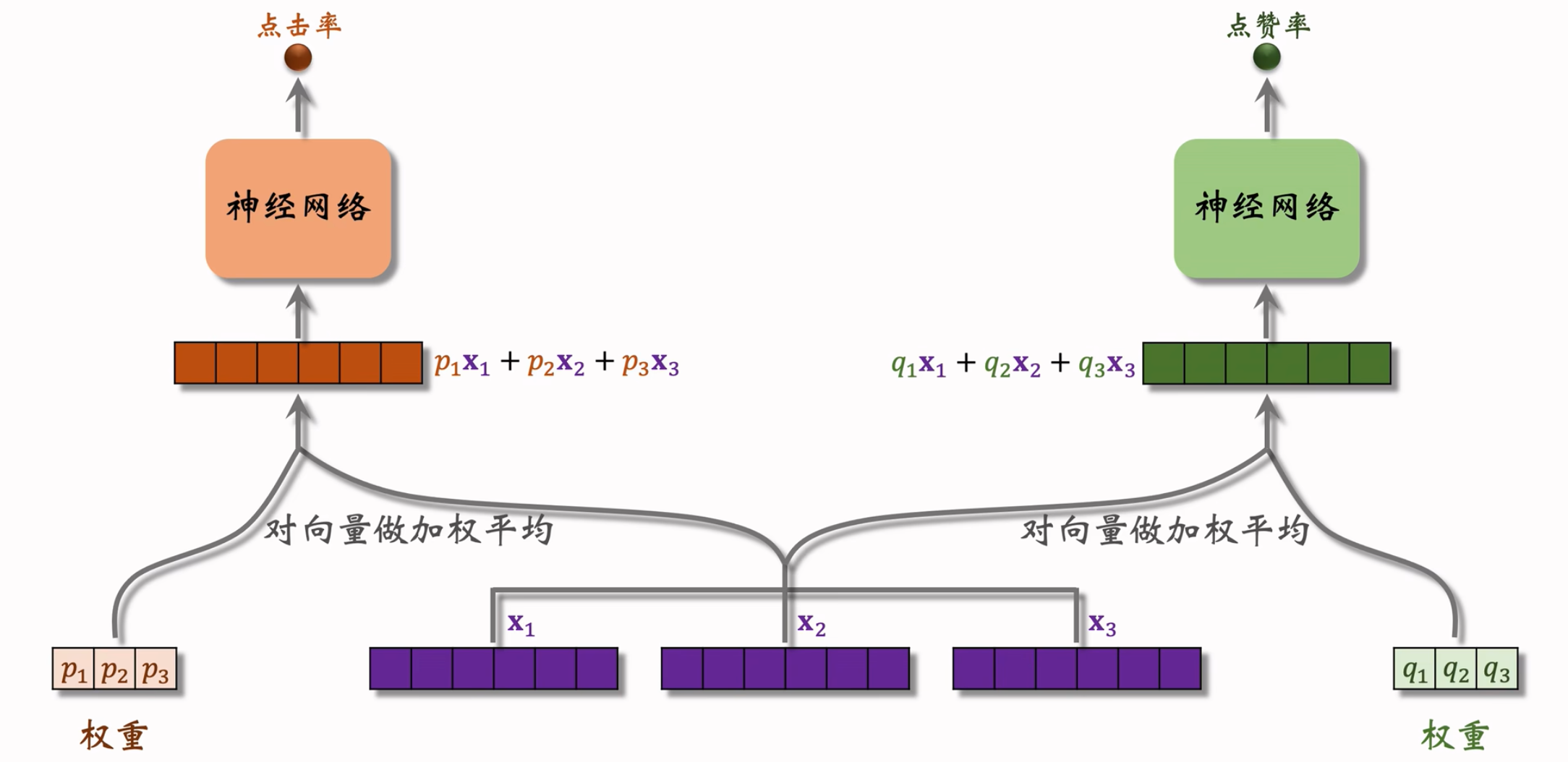
每一个指标,都会有一组专门的权重,负责处理多个Experts的输出,并最终输出这个指标的预估值。
极化现象(Polarization)
专家神经网络在实践中的问题。
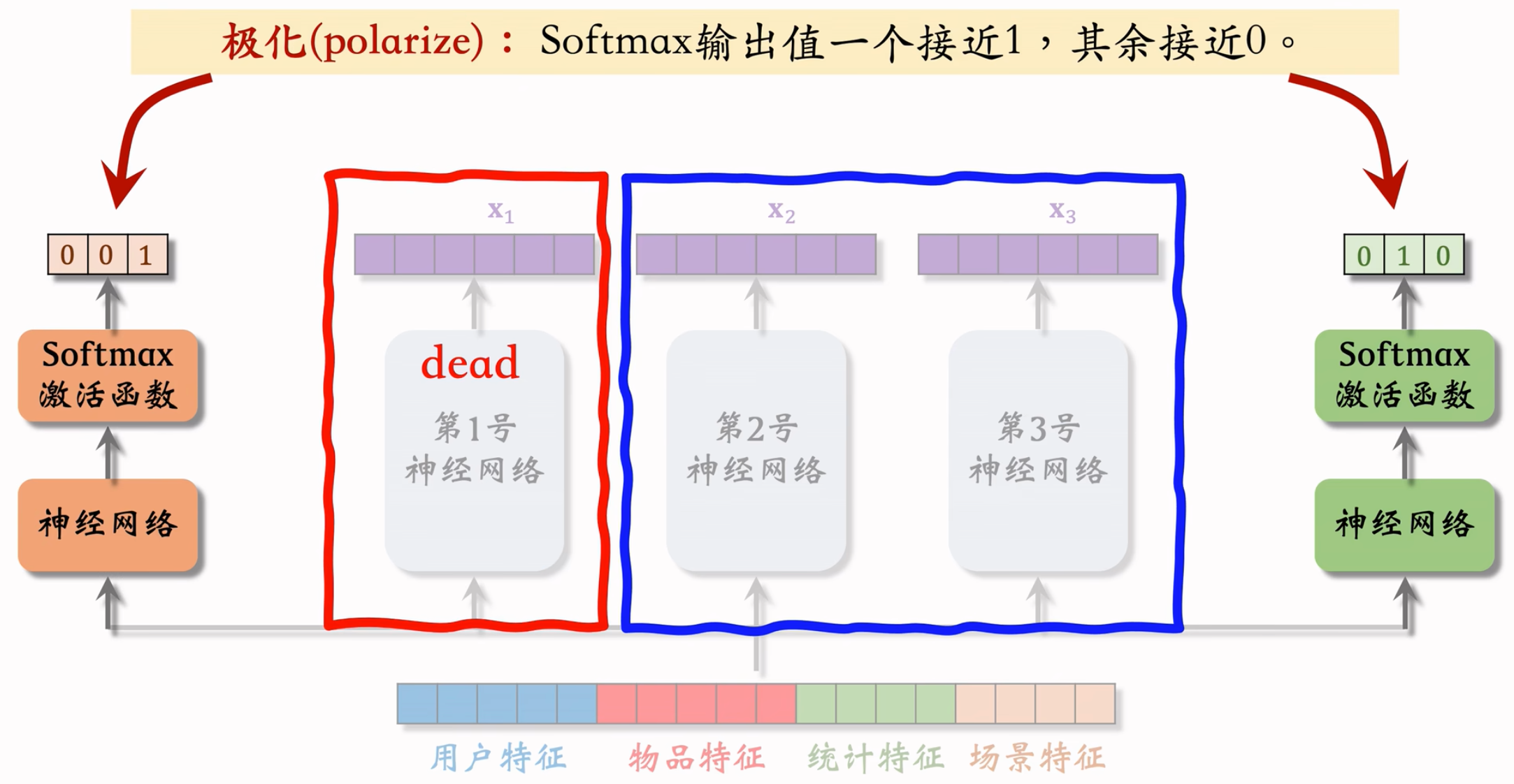
不同的权重,在多个指标下,使得某个神经网络没有被用到,或者用到的特别少。就相当于没有对专家做融合嘛,没有起到MoE的优势。
解决极化问题的方法:
- 如果有 $n$ 个“专家”,那么每个 softmax 的输入和输出都是 $n$ 维向量
- 在训练时,对 softmax 的输出使用 dropout
- Softmax 输出的 $n$ 个数值被 mask 的概率都是 10%
- 每个“专家”被随机丢弃的概率都是 10%
- 由于每个“专家”都可能被丢弃,神经网络在训练过程中没法过度依赖某个“专家”,神经网络就会尽量避免极化的发生。
实际应用场景中,MMoE用上了不一定会有提升。博主聊过,MMoE没效果的原因很多情况下不清楚,有可能是设计/应用场景的原因。很有可能是试过了但是不work!
参考文献:
- Jiaqi Ma et al.Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts.In KDD,2018.
- Zhe Zhao et al.Recommending What Video to Watch Next:A Multitask Ranking System.In RecSys, 2019.
Fusion of estimated scores
简单的加权:$p_{click}+w_1·p_{like}+w_2·p_{collect}+…$
点击率乘以其他项的加权和 $p_{click}·(1+w_1·p_{like}+w_2·p_{collect}+…)$
- $p_{click}=\frac{点击}{曝光}$,$p_{like}=\frac{点赞}{点击}$
- 所以 $p_{click}·p_{like}=\frac{点赞}{曝光}$(类似于贝叶斯的想法)
海外某短视频 APP 的融分公式 : $(1+w_{1}\cdot p_{time})^{\alpha_{1}}\ \cdot\ \ (1+w_{2}\cdot p_{like})^{\alpha_{2}}\ \cdots$,这里$\omega_1,\ \alpha_1$都是超参数。
国内某短视频 APP (老铁)的融分公式
- 根据预估时长 $p_{time}$,对 $n$ 篇候选视频做排序
- 如果某视频排名第 $r_{time}$,则它得分 $\frac{1}{r^\alpha _{time} +\beta}$
- 对点击、点赞、转发、评论等预估分数做类似处理
- 最终融合分数: $\frac{w_{1}}{r_{\mathrm{time}}^{\alpha_{1}}+\beta_{1}}\ +\ \frac{w_{2}}{r_{\mathrm{click}}^{\alpha_{2}}+\beta_{2}}\ +\ \frac{w_{3}}{r_{\mathrm{like}}^{\alpha_{3}}+\beta_{3}}\ +\ \cdots$
- 公式特点在于 — 不是用预估的分数,而是使用预估的排名。
某电商的融分公式
- 电商的转化流程:曝光 → 点击 → 加购物车 → 付款
- 模型预估:$p_{click}$、$p_{cart}$、$p_{pay}$
- 最终融合分数: $p_{\mathrm{cilck}}^{\alpha_{1}}\ \times\ \ p_{\mathrm{cart}}^{\alpha_{2}}\ \times\ \ p_{\mathrm{pay}}^{\alpha_{3}}\ \times\ \mathrm{price}^{\alpha_{4}}$
- 假如 $\alpha_{1}=\alpha_{2}=\alpha_{3}=\alpha_{4}=1$ 那该公式就是电商的营收,有明确的物理意义。
Video play modeling
视频播放时长
图文 vs. 视频
- 图文笔记排序的主要依据:点击、点赞、收藏、转发、评论……
- 视频排序的依据还有播放时长和完播 ,对于视频来说,播放时长与完播的重要性大于点击。
- 直接用回归拟合播放时长效果不好。建议用 YouTube 的时长建模
参考:Paul Covington, Jay Adams, & Emre Sargin. Deep Neural Networks for YouTube Recommendations. In RecSys, 2016.
模型:
模型结构:
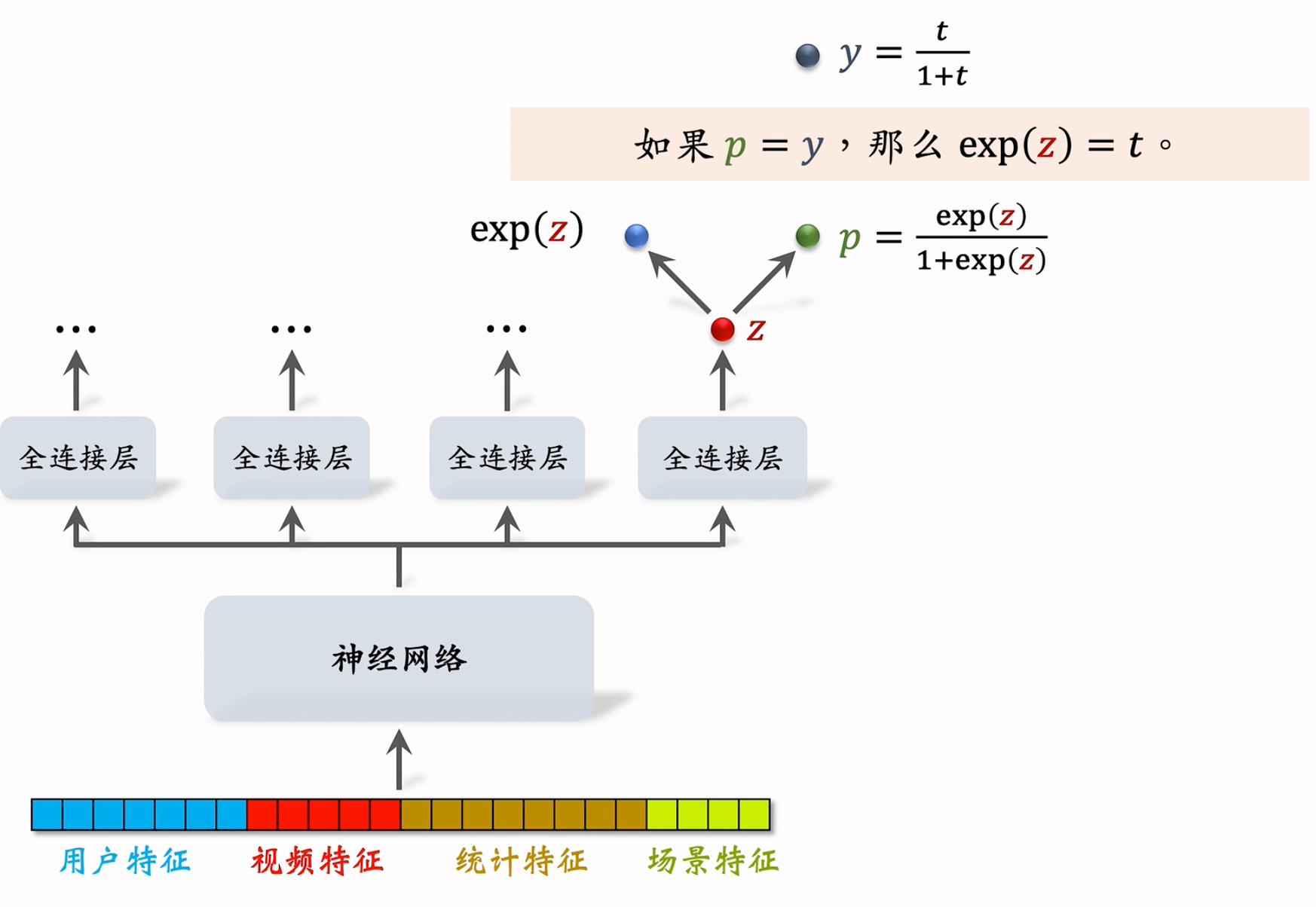
每个全连接层对应一个目标,假设最右边的输出对应播放时长 $z$, 对 $z$ 做 Sigmoid 变换得到 $p$,然后让 $p$ 拟合 $y$,它们的交叉熵作为损失函数。 $y$ 是我们定义的,其中的 $t$ 是用户实际观看时长,$t$ 越大则 $y$ 越大。目标就是要让p逼近于y。
观察公式发现
如果 $p=y$,那么 $\exp{(z)}=t$ ,即 $\exp{(z)}$ 就是播放时长的预估值。
总结视频播放时长建模
- 把最后一个全连接层的输出记作 $z$。设 $p=sigmoid(z)$
- 实际观测的播放时长记作 $t$。(如果没有点击,则 $t = 0$)
- 做训练:最小化交叉熵损失 $-\left({\frac{t}{1+t}}\cdot\log p+{\frac{1}{1+t}}\cdot\log(1-p)\right)$
- 实践中可以去掉分母 $1+t$,就等于给损失函数做加权,权重是播放时长。
- 做推理:把 $exp(z)$ 作为播放时长的预估。最终把 $exp(z)$ 作为融分公式中的一项。
说白了就是想训练一个能够预估视频播放时长的模型呗。然后这个指标就成为我们预估视频质量分数的一个指标!
视频完播
回归方法
- 视频长度 10 分钟,实际播放 4 分钟,则实际播放率为 𝑦 = 0.4
- 让预估播放率 $p$ 拟合 $y$:$\textstyle{loss}=y\cdot\log p+(1-y)\cdot\log(1-p)$
- 线上预估完播率,模型输出 $p$ = 0.73,意思是预计播放 73%
二元分类方法
- 自定义完播指标,比如完播 80%
- 例:视频长度 10 分钟,播放 > 8 分钟作为正样本,播放 < 8 分钟作为负样本
- 做二元分类训练模型:播放 > 80% vs 播放 < 80%
- 线上预估完播率,模型输出 $p$ = 0.73,意思是$\mathbb{P}(播放>80%)=0.73$
不能直接把完播率当作指标,视频越长,完播率越低。利好与短视频,对长视频不公平!
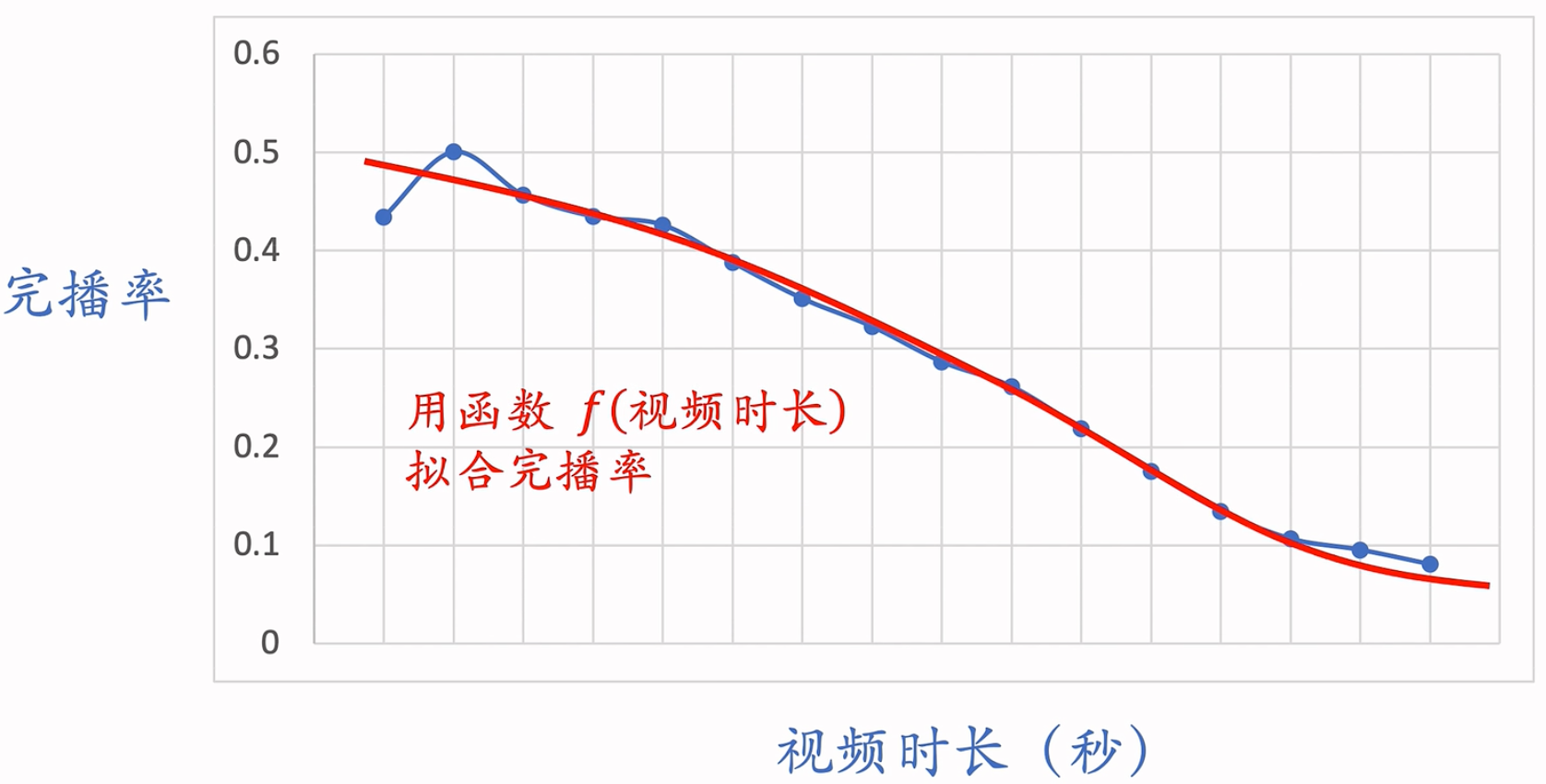
拟合完播率,统一量纲,让它make sense!
- 预估完播率,然后做调整,$p_{finish} = \frac{预估完播率}{f(视频长度)}$,这里的$f$就是上面的拟合曲线。
- 可以把这里的$p_{finish}$作为融分公式中的一项。
Characteristics of ranking models
用户画像(User Profile)
- 用户 ID(在召回、排序中做 embedding,用户 ID 本身不携带任何信息,但模型学到的 ID embedding 对召回和排序有很重要的影响)
- 人口统计学属性:性别、年龄
- 账号信息:新老、活跃度……(模型需要专门针对 新用户 和 低活跃 用户做优化)
- 感兴趣的类目、关键词、品牌(对排序很有用)
物品画像(Item Profile)
- 物品 ID(在召回、排序中做 embedding,非常重要)
- 发布时间(或者年龄,越久越没价值,尤其是时效性低的信息)
- GeoHash(经纬度编码)、所在城市
- 标题、类目、关键词、品牌…… (通常对于这些离散的信息做Embedding)
- 字数、图片数、视频清晰度、标签数…… (笔记自带属性,反映笔记的质量)
- 内容信息量、图片美学…… (算法打的分数,事先用人工标注的数据训练 NLP 和 CV 模型,然后用模型打分)
用户统计特征
- 用户最近 30 天(7 天、1 天、1 小时)的曝光数、点击数、点赞数、收藏数……(划分各种时间粒度,可以反映用户的 实时、短期、中长期 兴趣)
- 按照笔记图文/视频分桶。(比如最近 7 天,该用户对图文笔记的点击率、对视频笔记的点击率。可以反映用户对两类笔记的偏好)
- 按照笔记类目分桶。(比如最近 30 天,用户对美妆笔记的点击率、对美食笔记的点击率、对科技数码笔记的点击率,反映用户对哪个类目更感兴趣。)
笔记统计特征
- 笔记最近 30 天(7 天、1 天、1 小时)的曝光数、点击数、点赞数、收藏数……(划分时间粒度,可以提前发现哪些笔记过时了)
- 按照用户性别分桶、按照用户年龄分桶……
- 作者特征:发布笔记数、粉丝数、消费指标(曝光数、点击数、点赞数、收藏数)
场景特征(Context)
- 用户定位 GeoHash(经纬度编码)、城市
- 当前时刻(分段,做 embedding)
- 一个人在同一天不同时刻的兴趣是变化的。
- 而且可以反推用户是在上班路上、公司、家里
- 是否是周末、是否是节假日
- 手机品牌、手机型号、操作系统
- 安卓用户和苹果用户的 点击率、点赞率 等数据差异很大
特征处理
- 离散特征:做 embedding
- 用户 ID、笔记 ID、作者 ID
- 类目、关键词、城市、手机品牌
- 连续特征: 做分桶,变成离散特。年龄、笔记字数、视频长度。
- 离散特征:做 embedding
其他变换
- 曝光数、点击数、点赞数等数值具有长尾效应,做 $\log{(1+x)}$。
- 转化为点击率、点赞率等值,并做平滑。
特征覆盖率
- 很多特征无法覆盖 100% 样本
- 例:很多用户不填年龄,因此用户年龄特征的覆盖率远小于 100%
- 例:很多用户设置隐私权限,APP 不能获得用户地理定位,因此场景特征有缺失
- 提高特征覆盖率,可以让精排模型更准
- 想各种办法提高特征覆盖率,并考虑特征缺失时默认值如何设置
数据服务:
三个数据源:用户画像(User Profile)、物品画像(Item Profile)、统计数据。三个数据源都存储在内存数据库中。
线上服务的时候,排序服务器会从三个数据源取回所需要的数据,然后把读取的数据做处理,作为特征喂给模型。模型就能够预估出点击率、点赞率等指标。
整体流程图:
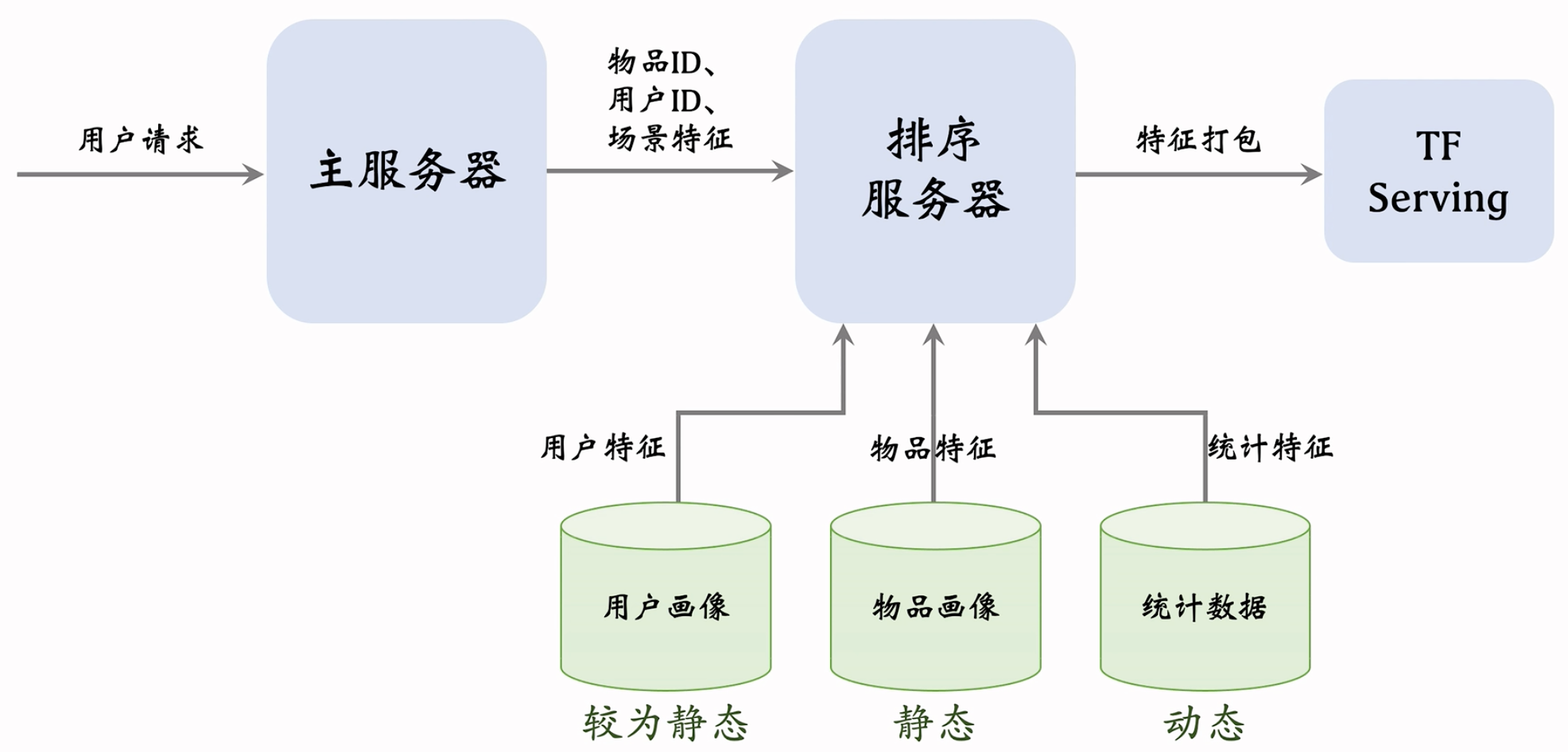
用户画像数据库压力小(每次只读 1 个用户),物品画像数据库压力非常大(每次读几千个物品) 。工程实现时,用户画像中的特征可以很多很大,但尽量不往物品画像中塞很大的向量。
由于用户和物品画像较为静态,甚至可以把用户和物品画像缓存在排序服务器本地,加速读取
收集了排序所需特征后,将特征打包发给 TF Serving,Tensorflow 给笔记打分并把分数返回排序服务器
排序服务器依据融合的分数、多样性分数、业务规则等给笔记排序,并把排名最高的几十篇返回主服务器
Rough Sort
上面这些精排用的多,下面讲讲粗排
粗排 vs 粗排:
粗排:给几千篇笔记打分,单次推理代价必须小,预估的准确性不高。
精排:给几百篇笔记打分,单次推理代价很大,预估的准确性更高。
模型简介:
精排模型:
模型结构:
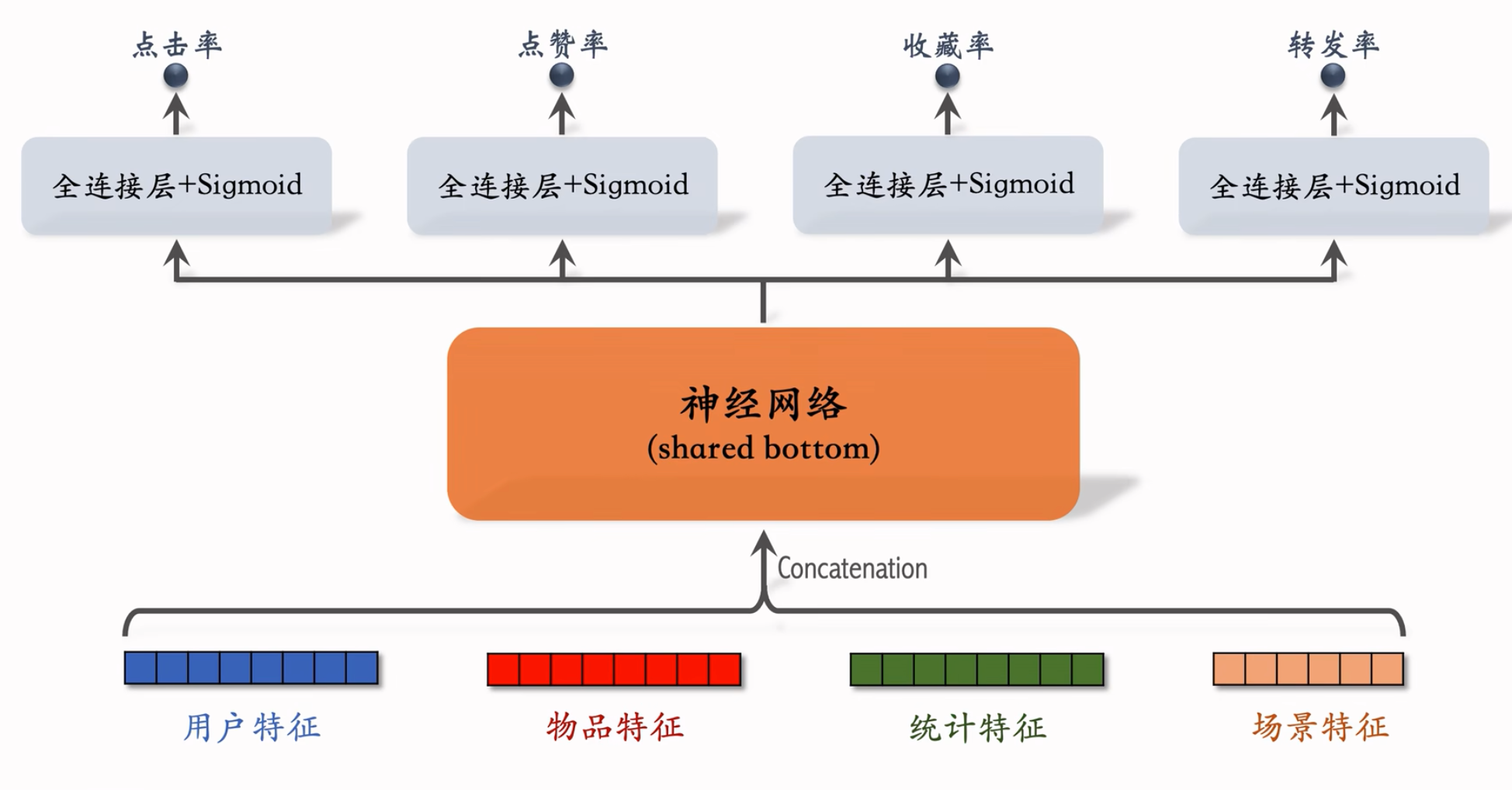
直接对各种特征做concatenation,塞入shared bottom中,意思是它被多个任务共享。再接上多个头,得到每个指标。
开销主要在shared button,它很大,模型很复杂。
前期融合:先对所有特征做 concatenation,再输入神经网络。
线上推理代价大:如果有 $n$ 篇候选笔记,整个大模型要做 $n$ 次推理。
双塔模型:
模型结构:
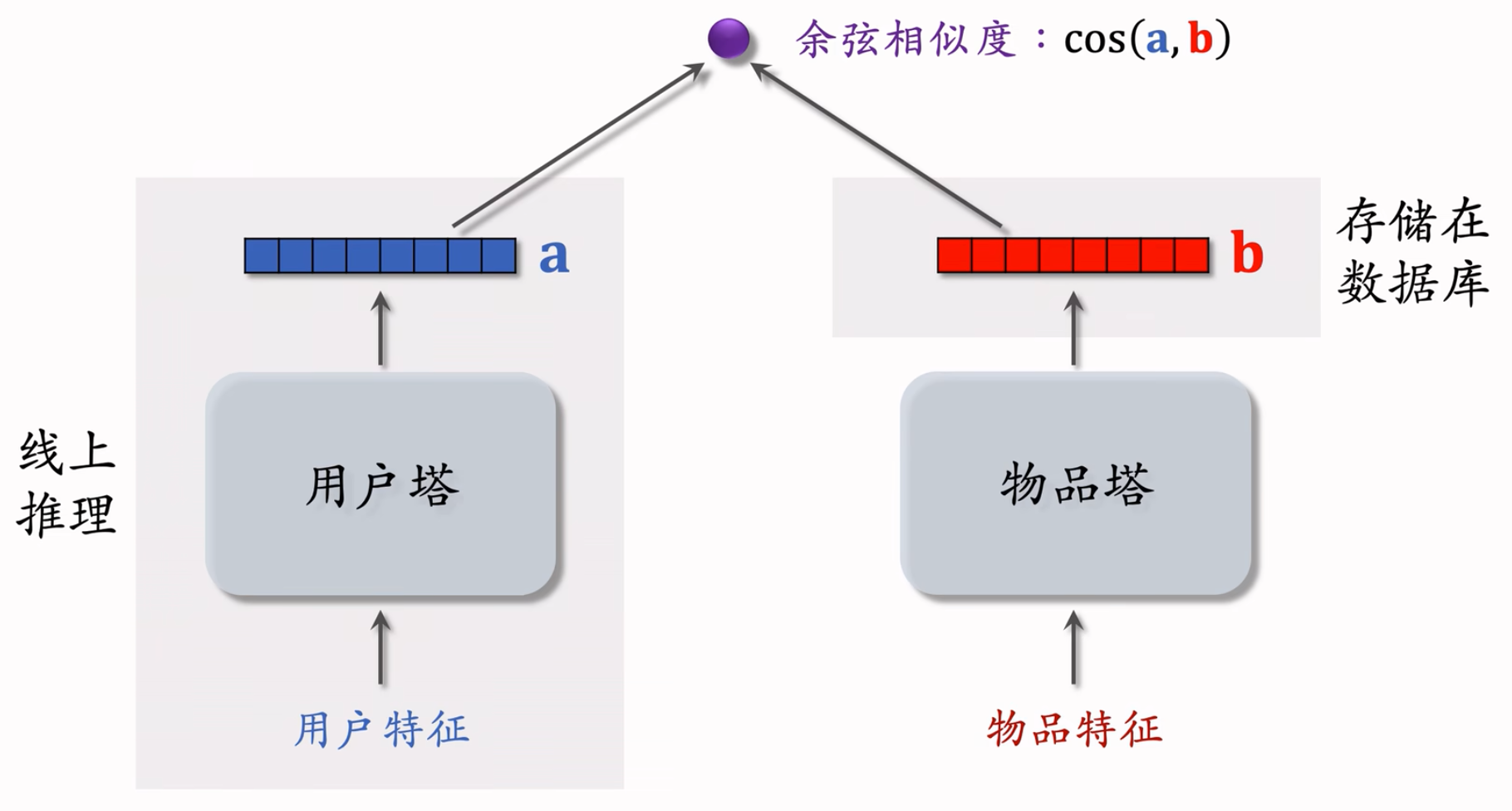
物品塔在训练结束后,物品其实就可以直接过物品塔,然后存储到向量数据库中了。线上不需要用物品塔做计算。
线上只需要用到用户塔,每做一次推荐,用户塔只做一次推理,得到一个向量。而且本身塔的结构较为简单,计算代价很小,适合做召回。
后期融合:把用户、物品特征分别输入不同的神经网络,不对用户、物品特征做融合 。
线上计算量小:
- 用户塔只需要做一次线上推理,计算用户表征 $\bold{a}$
- 物品表征 $\bold{b}$ 事先储存在向量数据库中,物品塔在线上不做推理
后期融合模型不如前期融合模型准确
- 预估准确性不如精排模型
- 后期融合模型用于召回,前期融合模型用于精排。
粗排的三塔模型:
小红书粗排用的三塔模型,效果介于双塔和精排之间。[参考文献](参考文献:Zhe Wang et al. COLD: Towards the Next Generation of Pre-Ranking System. In DLP-KDD, 2020.)
模型结构:
交叉特征:用户特征与物品特征做交叉。
对 3 个塔输出的向量做Concatenation 和 Cross(交叉)得到 1 个向量。
与前期融合在最开始对各类特征做融合不同,三塔模型在塔输出的位置做融合。
模型各个部分的计算量:
- 通常来说,交叉塔必须足够小(通常只有一层,参数也小),速度够快。
有 $n$ 个物品,模型上层需要做 $n$ 次推理,粗排推理的大部分计算量在模型上层:这个环节无法利用缓存节省计算量,三塔模型节省的是对物品推理的计算量。
三塔模型的推理
- 从多个数据源取特征:1 个用户的画像、统计特征。$n$ 个物品的画像、统计特征
- 用户塔:只做 1 次推理
- 物品塔:未命中缓存时需要做推理 。(最坏情况下,需要做n次推理,但实际上缓存命中率非常高,99%都能命中缓存,不需要做推理。给几千个候选物品做粗排,物品塔只需要做几十次推理。)
- 交叉塔:必须做 $n$ 次推理
- 上层网络做 $n$ 次推理,给 $n$ 个物品打分
- 粗排模型的设计理念就是尽量减少推理的计算量,使得模型可以线上对几千篇笔记打分
Feature Crossover
Factorized Machine (FM)
FM 以前在召回和排序都很常用,现在用得少了,主要了解一下思想。特征交叉有必要,可以让模型变得很准确!
线性模型
- 有 $d$ 个特征,记作 $\mathbf{x}=\left[x_{1},\cdot\cdot\cdot,x_{d}\right]$
- 线性模型:$p\ =\ b\ +\textstyle{\sum_{i=1}^{d}}w_{i}x_{i}$ ,$b$ 是偏移项 bias
- 模型有 $d+1$ 个参数:${\bf w}=\left[{\bf w}{1},\cdot\cdot\cdot,{\bf w}{d}\right]$ 和 $b$
- 预测是特征的加权和(只有加,没有乘) ,即特征之间没有交叉
二阶交叉特征
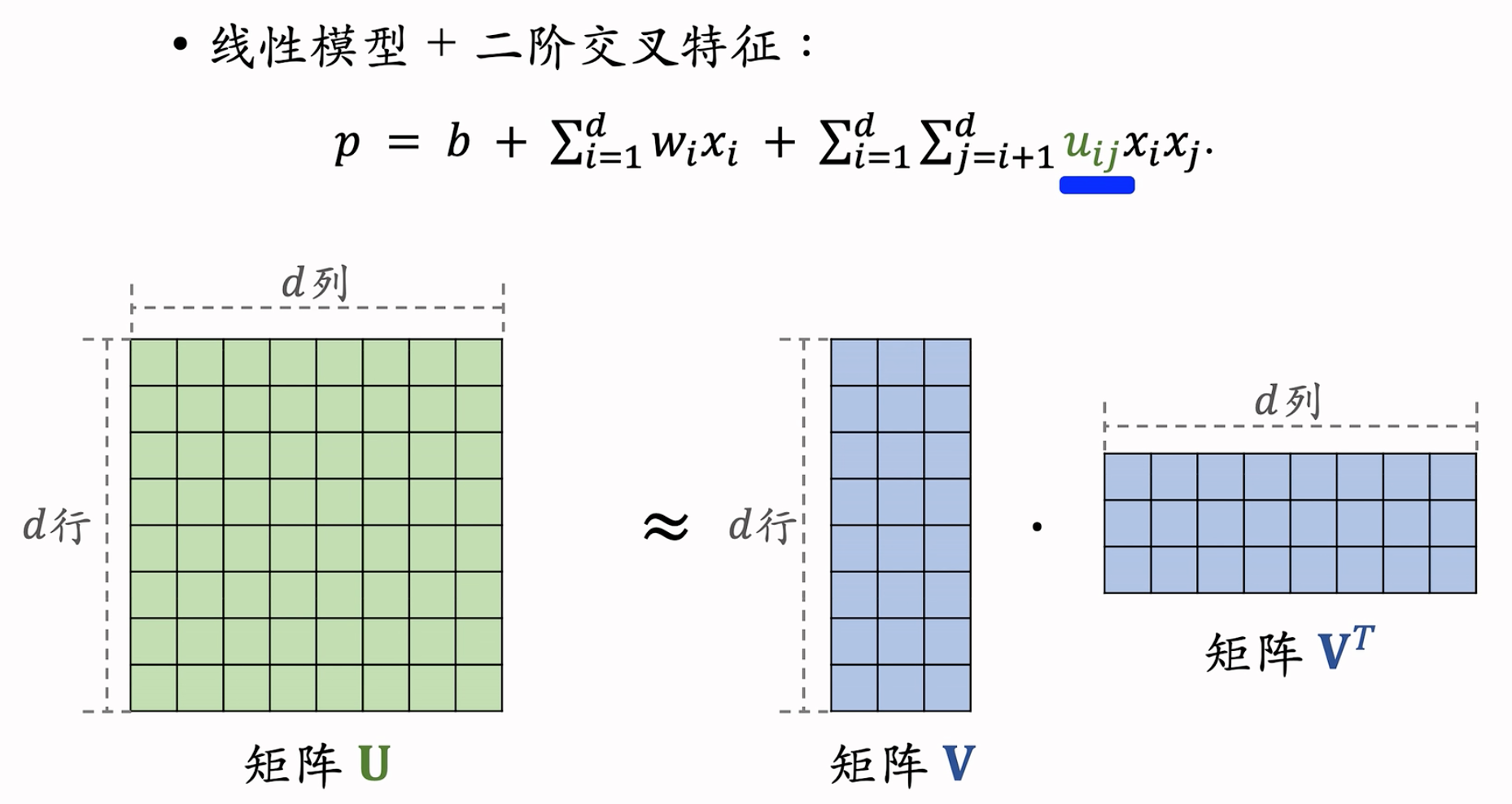
有 $d$ 个特征,记作 $\mathbf{x}=\left[x_{1},\cdot\cdot\cdot,x_{d}\right]$
线性模型 + 二阶交叉特征: $p=b+\sum_{i=1}^{d},w_{i}x_{i}+\sum_{i=1}^{d}\sum_{j=i+1}^{d}u_{ij}x_ix_j$ ,公式中的 $x_ix_j$ 就是两个特征的交叉,$u_{ij}$ 是权重。(例如:房子大小和每平米价格,交叉明显对于价格的预估更准确!)
模型有 $O(d^2)$ 个参数 ,$d$ 较大时,参数数量过多,且容易出现过拟合。减少参数!
减少参数的方式:
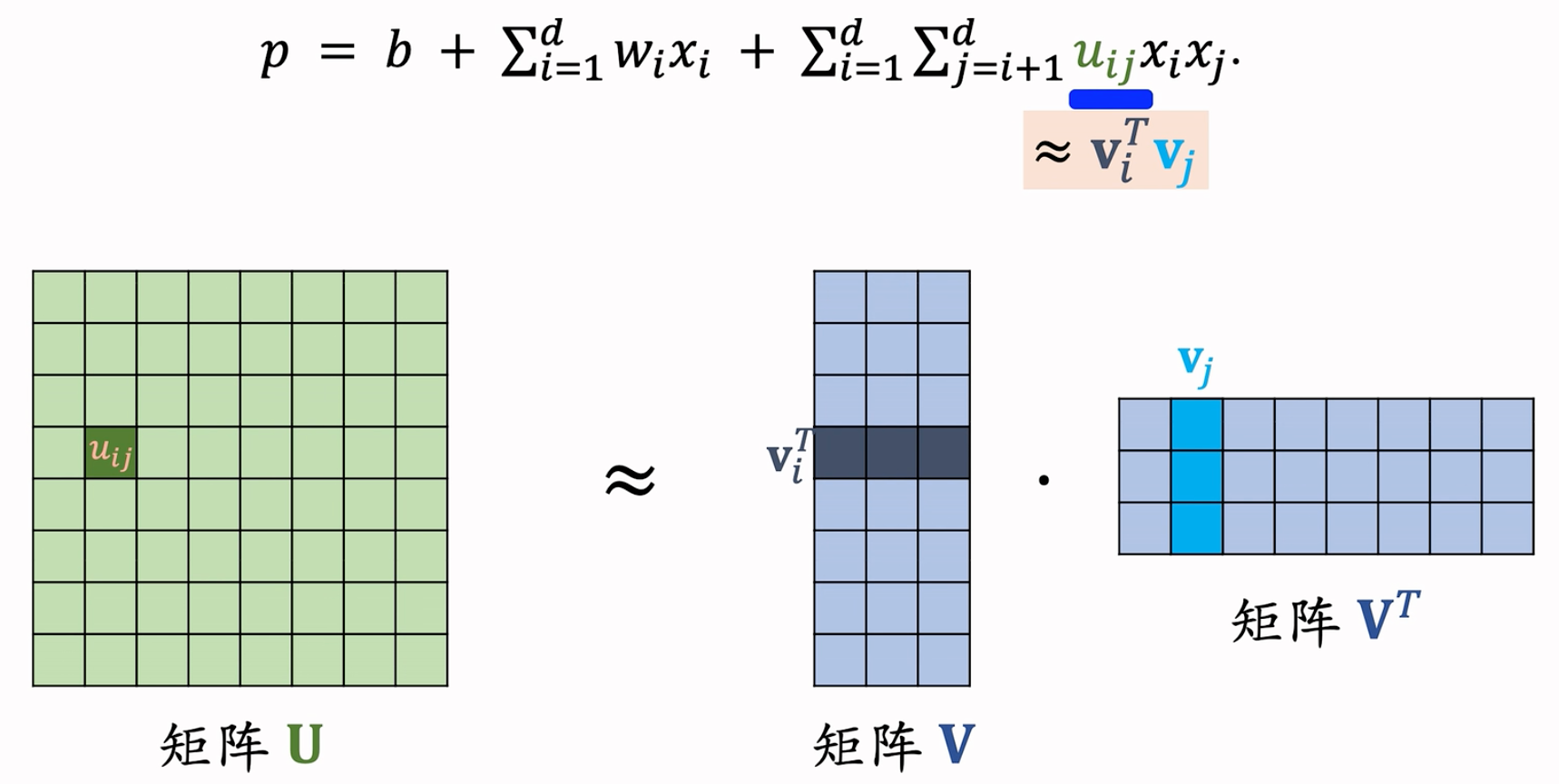
- Factorized Machine (FM): $p=b+\sum_{i=1}^{d},w_{i}x_{i}+\sum_{i=1}^{d}\sum_{j=i+1}^{d}(\bold{v}_i^T\bold{v}_j)x_ix_j$
- 使用矩阵 $\bold{V}\bold{V}^T$ 来近似矩阵 $\bold{U}$
- FM 模型有 $O(kd)$ 个参数($k\ll d$,是一个超参数),参数量从 $O(d^2)$ 降低到了 $O(kd)$ 。
总结:
- FM 是线性模型的替代品,能用线性回归、逻辑回归的场景,都可以用 FM。
- FM 使用二阶交叉特征,表达能力比线性模型更强
- 通过做近似 $u_{ij}\approx\bold{v}_i^T\bold{v}_j$,FM 把二阶交叉权重的数量从 $O(d^2)$ 降低到 $O(kd)$
- 早期的推荐系统通常使用LR,在LR中用FM做特征交叉,流行了很长一段时间。但是现在工业界里面,FM的这种做法已经过时了。小红书里面早都下掉了FM。
参考文献:Steffen Rendle.Factorization machines. In ICDM, 2010.
Deep & Cross Networks (DCN)
Deep & Cross Networks (DCN) 译作“深度交叉网络”,可以用于召回双塔模型、粗排三塔模型、精排模型。DCN 由一个深度网络和一个交叉网络组成,交叉网络的基本组成单元是交叉层 (Cross Layer)。这节课最重点的部分就是交叉层。
双塔/三塔的每一个塔,精排多目标排序模型的shared bottom,排序MMoE模型的每一个神经专家网络。都可以使用任意的网络结构,最简单就是全连接,但是也可以用更加复杂/有效的网络结构。
交叉层(Cross Layer)
网络结构:
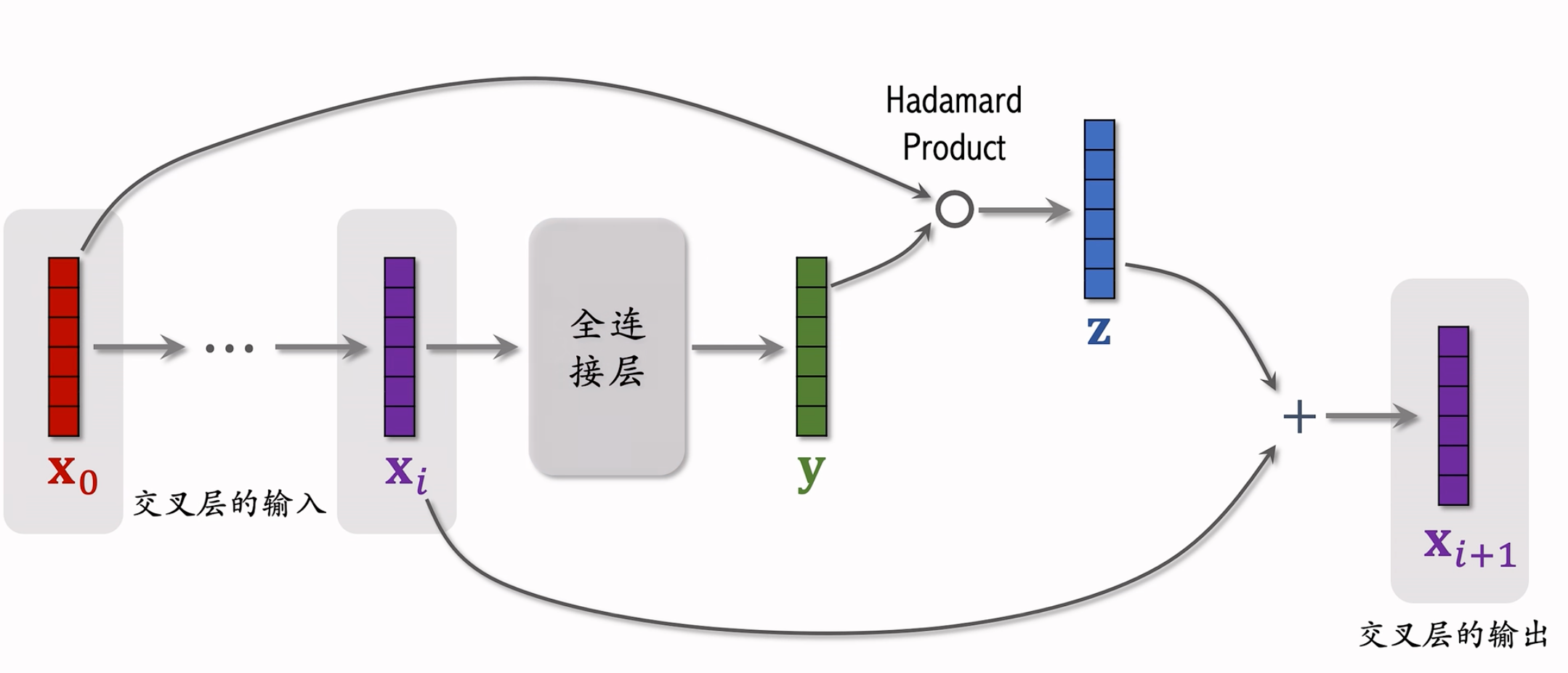
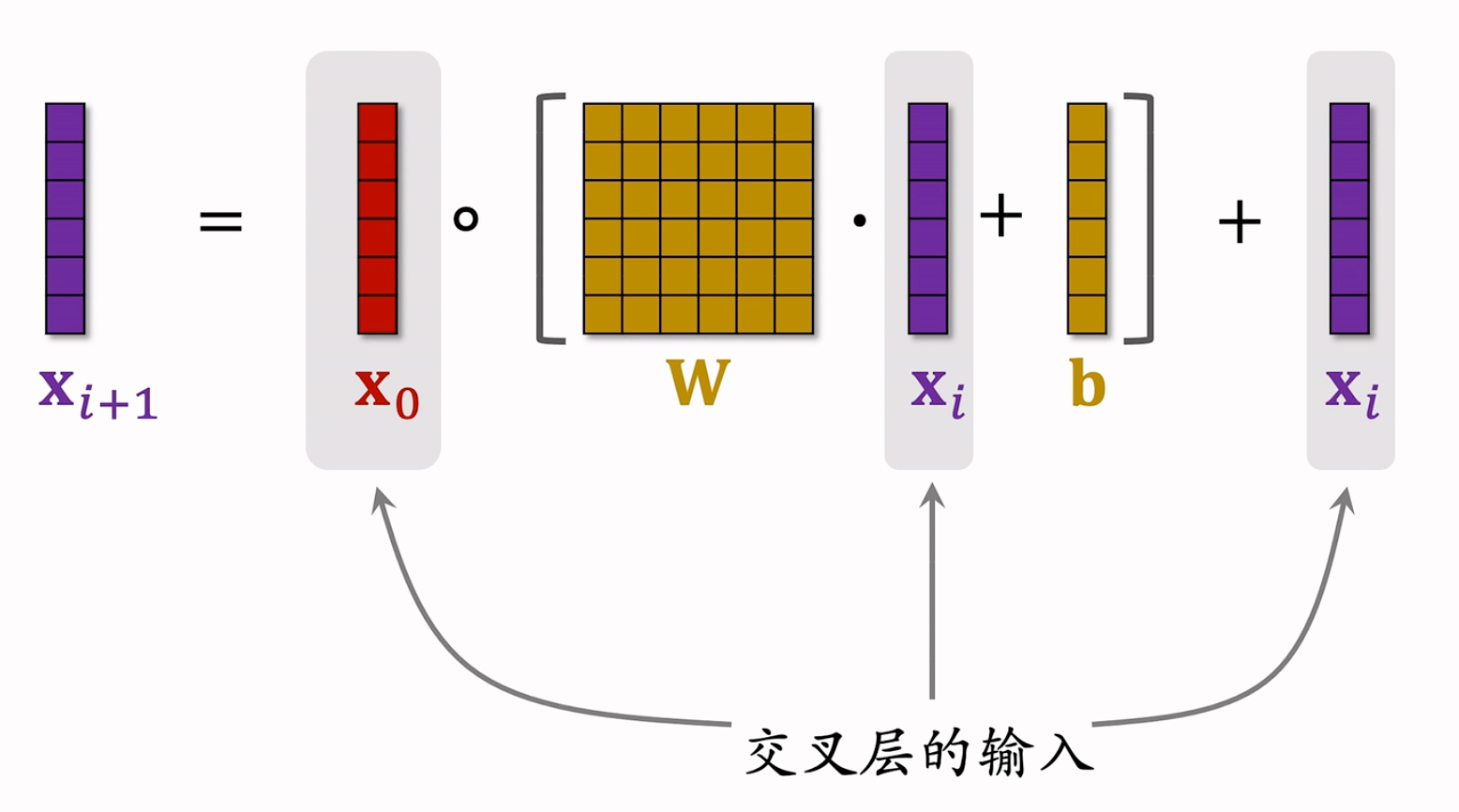
Hadmamard Product是逐元素相乘,要求矩阵的shape完全一致!有点类似于 ResNet 中的 跳跃链接 Skip Connection,防止梯度消失。每个交叉层的输入和输出都是向量,并且形状相同。
交叉网络(Cross Network)
交叉网络由多个交叉层堆叠而来:
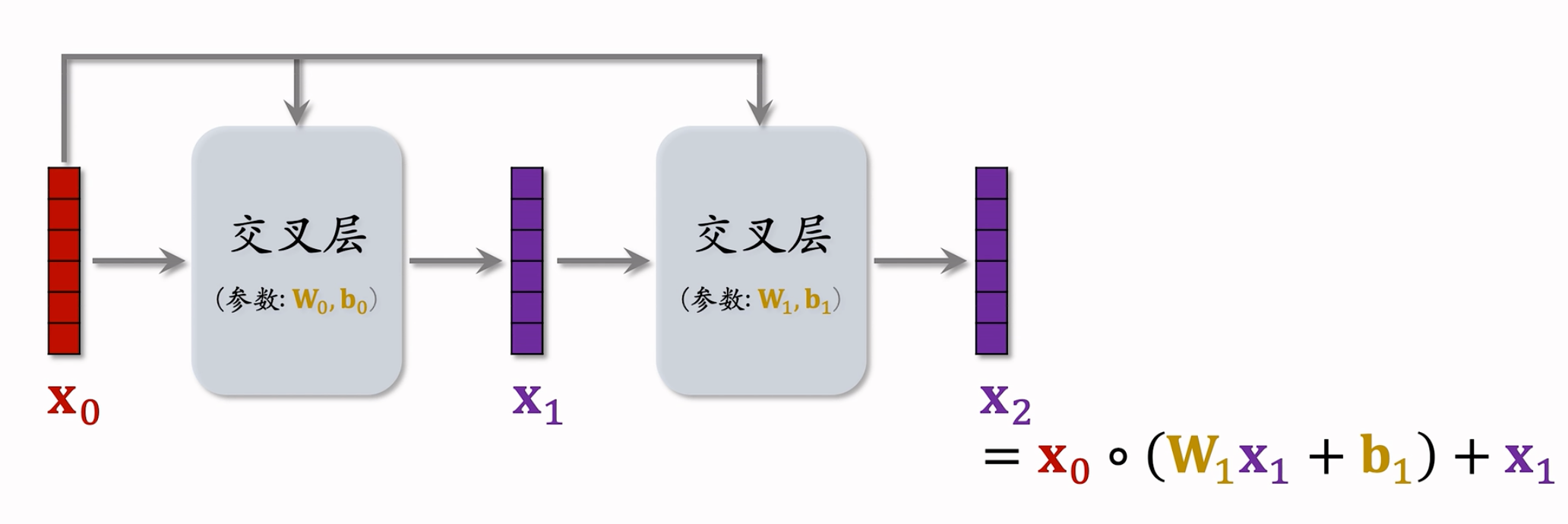
参考文献:这节课介绍的是 Cross Network V2,于2021年提出。老版本的 Cross Network是在2017年提出的。参考文献:
- Ruoxi Wang et al. DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems. In WWW, 2021.
- Ruoxi Wang et al. Deep & Cross Network for Ad Click Predictions. In ADKDD, 2017.
深度交叉网络DCN
网络结构:
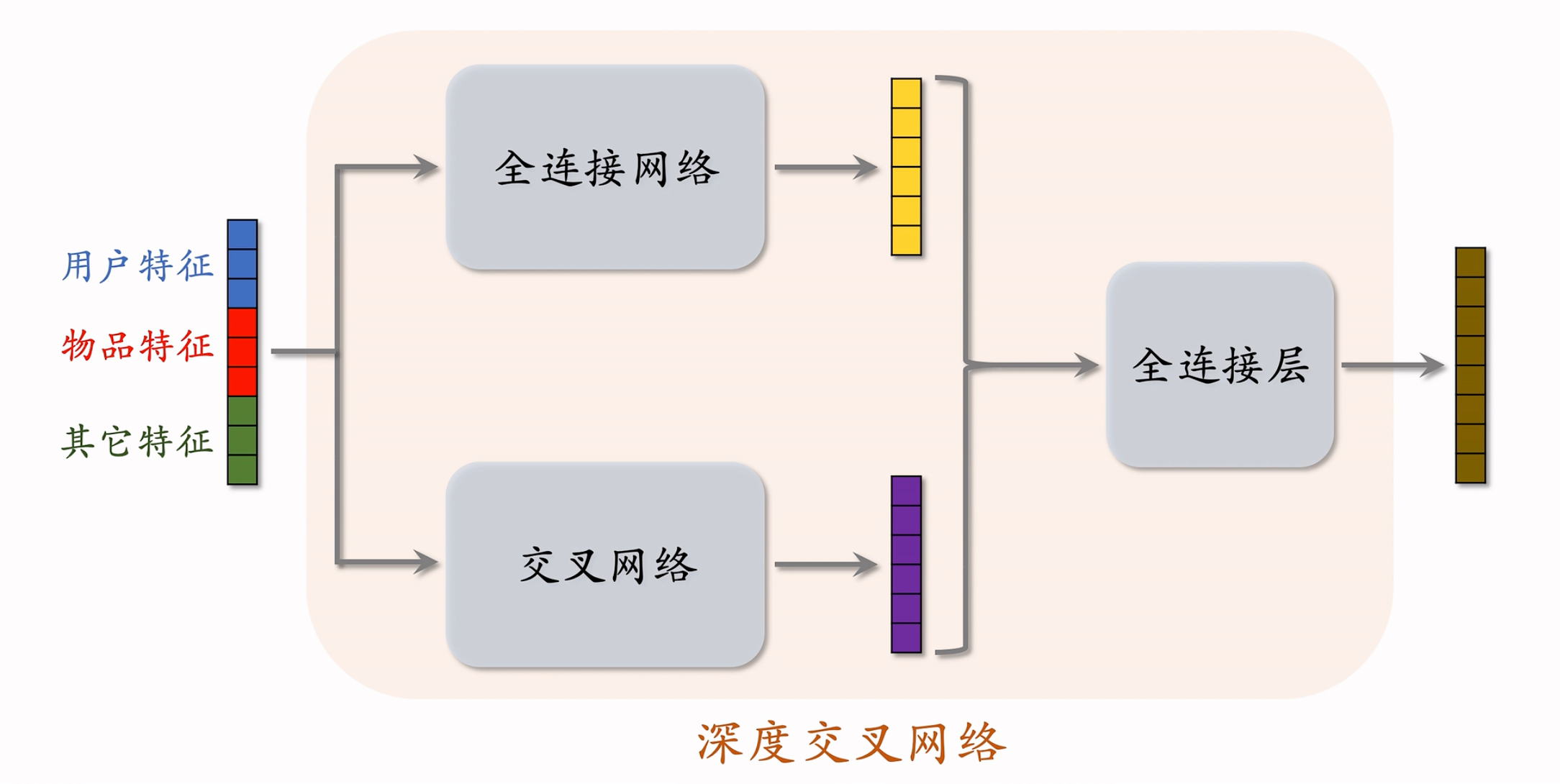
把 全连接网络、交叉网络、全连接层 拼到一起,就是 深度交叉网络 DCN。
比简单的全连接神经网络效果更好,被业界普遍接受,可以用于召回或者是排序。
召回、排序模型中的各种 塔、神经网络、专家网络 都可以是 DCN。
LHUC(PPNet)
LHUC 这种神经网络结构,可以用于精排。LHUC 的起源是语音识别,后来被应用到推荐系统,快手将其称为 PPNet,现在已经在业界广泛落地。视频中遗漏一个细节:将LHUC用于推荐系统,门控神经网络(2 x sigmoid)的梯度不要传递到用户ID embedding特征,需要对其做 stop gradient。
参考文献:
- Pawel Swietojanski, Jinyu Li, & Steve Renals. Learning hidden unit contributions for unsupervised acoustic model adaptation. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2016.
- 快手落地万亿参数推荐精排模型,2021。链接:https://ai.51cto.com/art/202102/644214.html
说话者的特征:例如说话者的 ID,年龄,性别 等
处理说话者的特征的神经网络
网络结构:
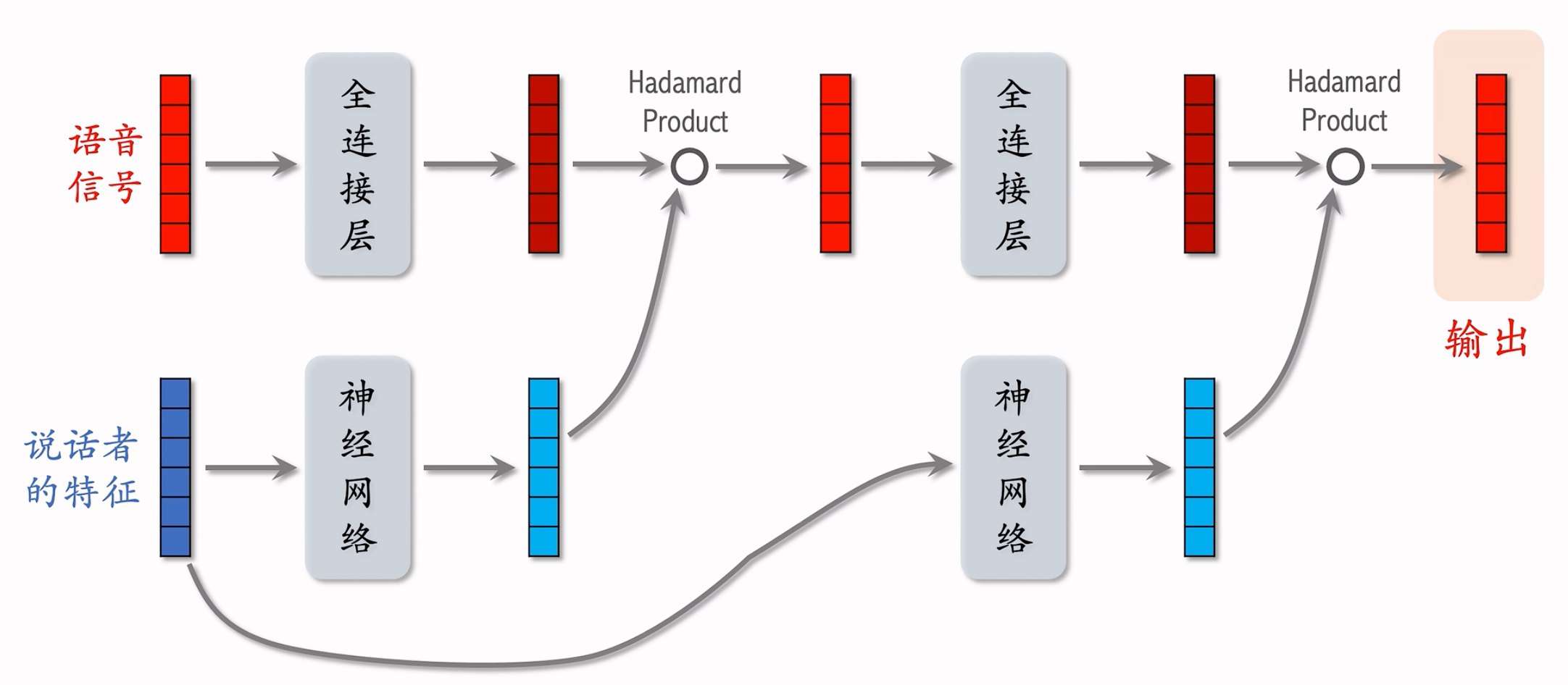
内部包含多个全连接层
下半部分的神经网络是由多个全连接层组成,激活函数是 Sigmoid 乘以 2,Sigmoid作用于每个元素上,Sigmoid输出的每个元素都介于[0, 2]。部分值大于 1,部分值小于 1,就可以拿去作为放缩因子,放大某些特征,缩小某些特征,实现个性化。
在推荐系统中:
模型结构:
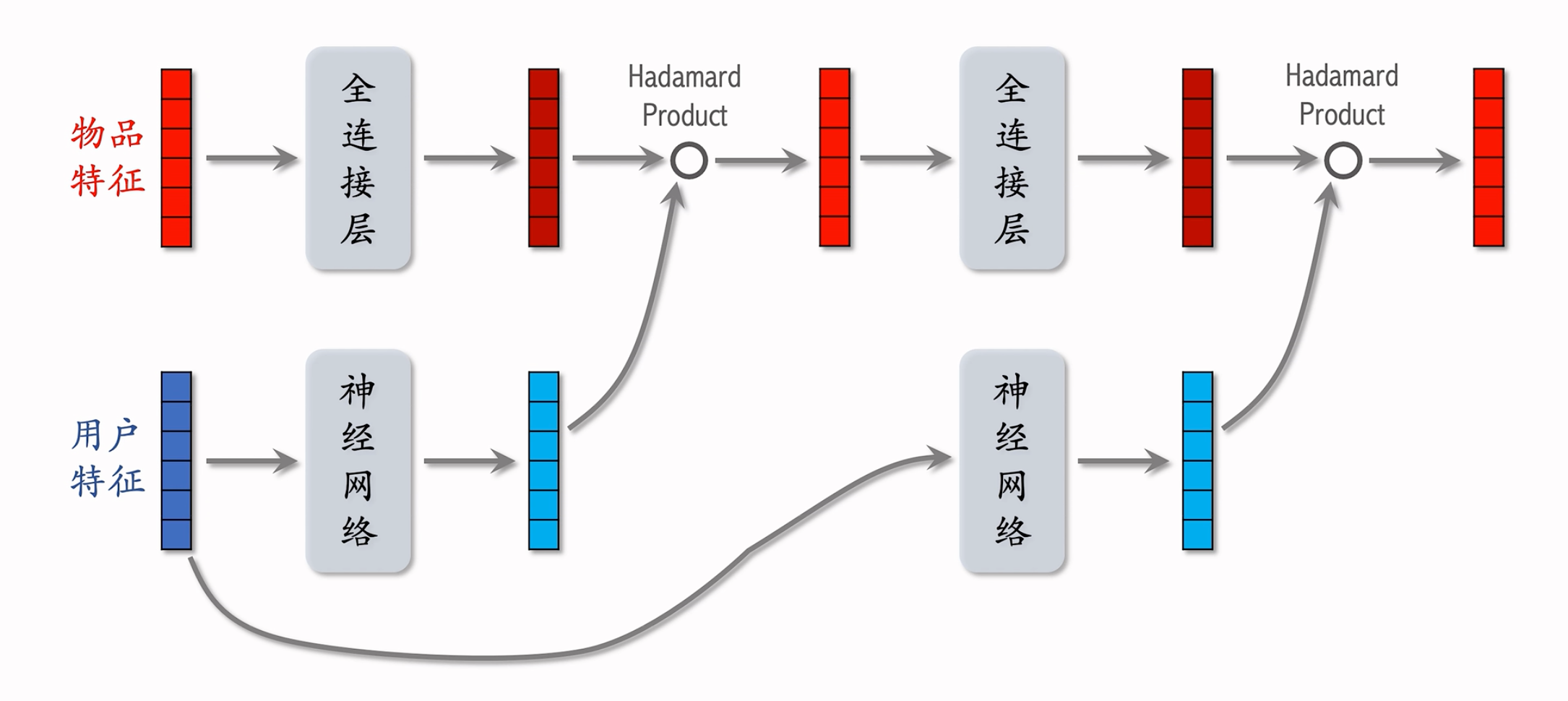
只是简单的把输入的特征活成了用户特征&物品特征。
SENet & Bilinear Cross
参考文献:
- Jie Hu, Li Shen, and Gang Sun. Squeeze-and-Excitation Networks. In CVPR, 2018.
- Tongwen Huang, Zhiqi Zhang, and Junlin Zhang. FiBiNET: Combining Feature Importance and Bilinear feature Interaction for Click-Through Rate Prediction. In RecSys, 2019.
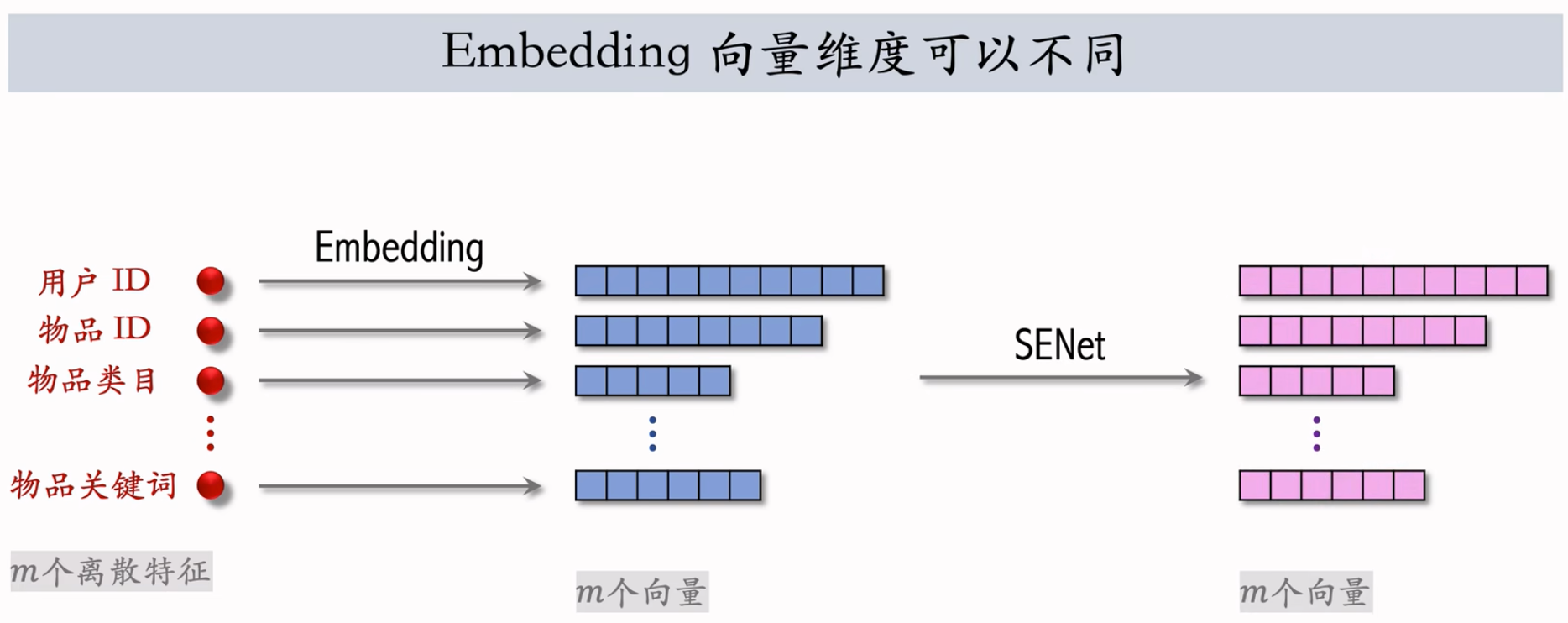
SENet
首先,把所有的m维离散的特征,做Embedding(假设dimension为k)会得到很多的向量(m x k),接下来SENet如何对这些Embedding做操作呢?
第一部分:
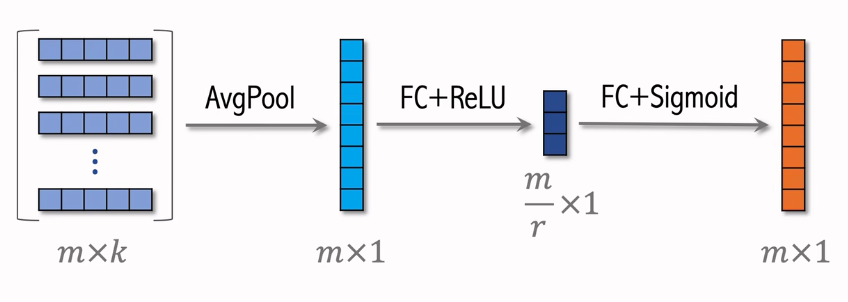
- $r$ 是压缩比列,设置为大于 1 的数。再用FC + Sigmoid,恢复出m维的向量。这个向量的元素都介于0和1之间。
- 原文中是按照特征通道的数量来进行压缩的,压缩后每个多维的特征通道变成一个实数,这个实数某种程度上具有全局的感受野。
- 给我的感觉其实就是attention哈哈哈哈哈,本质就是提取出里面的特征,再去算出来对每一个部分的“重视程度”。
第二部分:
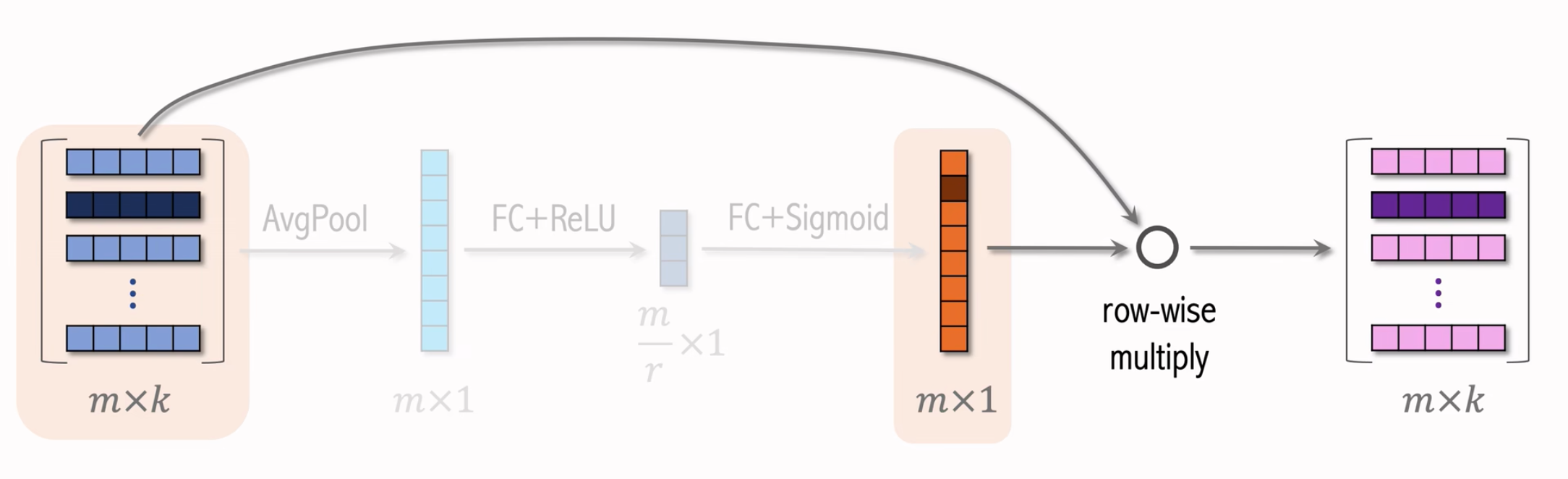
- 每个特征乘上对应这个特征的权重,拿到一个m x k的output。
- 使用右侧的 $m$ 维向量对左边矩阵的行做加权,赋予原始的Embedding对应的权重。
- 例如:学习发现物品 ID 对任务的重要性不高,就给物品 ID embedding 降权。
整体框架:
其实对于这m个特征,他们的Embedding向量维度可以不同,不会影响SENet。
框架图:
红色和蓝色的向量形状完全相同。
$m$ 个离散特征的 Embedding 向量维度可以不同。
SENet 本质是对离散特征做 field-wise 加权。Field 举例:
- 用户 ID Embedding 是 64 维向量。64 个元素算一个 field,获得相同的权重。
- 对于每一个Embedding,都对应了一个val(m x 1)权重,这个权重会作用于这个Embedding的每一个元素上,因此是field-wise的!
如果有 $m$ 个 fields,那么权重向量是 $m$ 维。
Field间特征交叉
最简单的特征交叉方法:
- 内积:假设m个fields,m x m,共得到$m ^ 2$个实数。$f_{ij} = x_{i}^{T} \times x_j$,还好,因为m就几十个。顶多产出几百个/几千个数字。
- 哈达玛乘积:假设m个fields,m x m,共得到$m ^ 2$个向量。$f_{ij} = x_{i} \bigodot x_j$,不太行,m就几十个。会产出几百个/几千个向量,这就有点夸张了。
- 两者都需要每个特征的Embedding向量维度一样,都是k维向量,不然算不了。
- 像哈达玛这种,就不能这么搞了,参数量太大。如果要用它做特征交叉,必须人工选择 tier 做交叉。
Bilinear Cross(内积)
更加先进的特征交叉方法。有内积和哈达玛乘积两种方式。
内积方式:
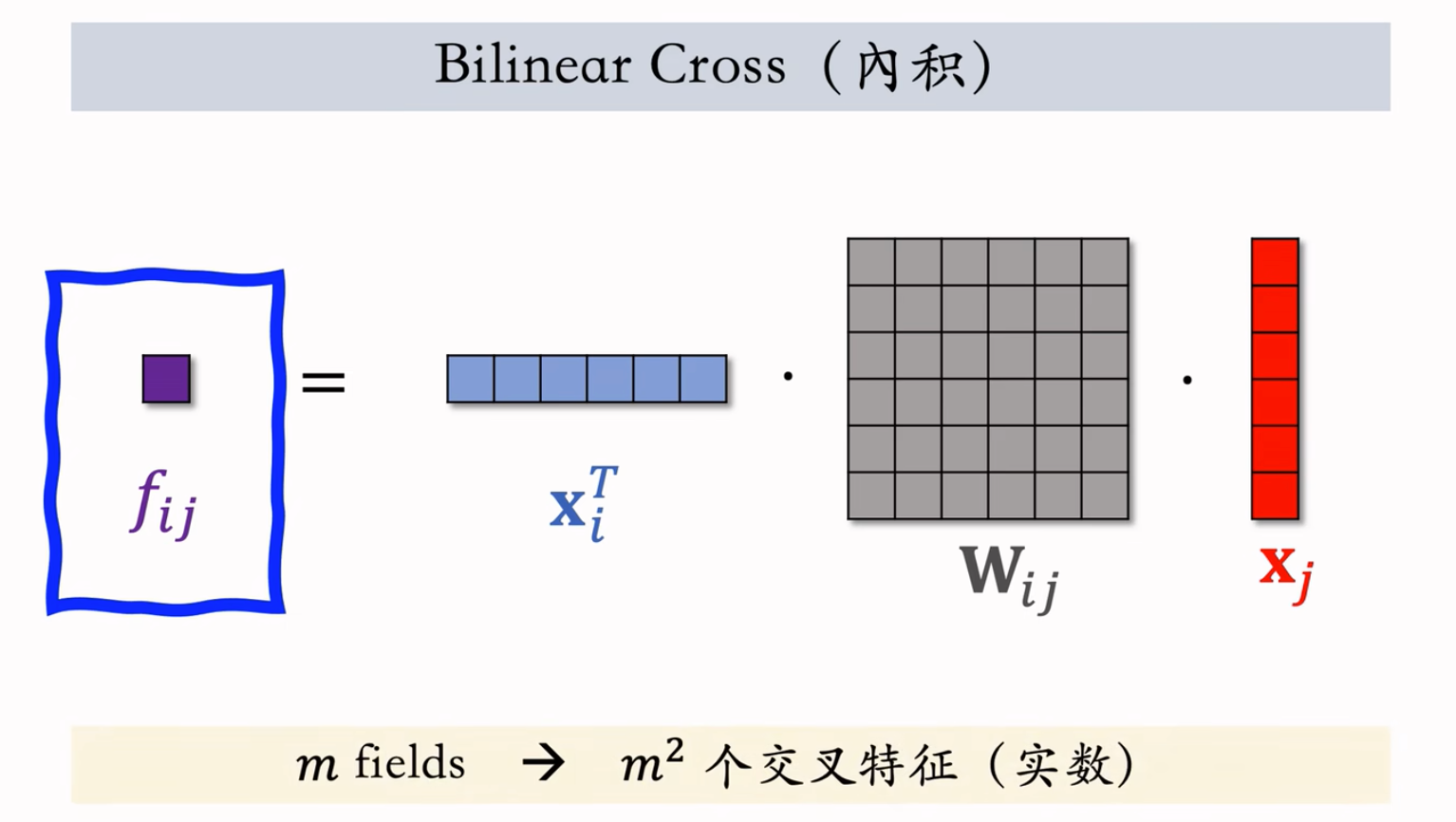
不要求特征形状相同
$m$ fields → $m^2$ 个交叉特征(实数) ,$m$ fields → $m^2/2$ 个参数矩阵。
参数矩阵过多,需要人工指定某些相关且重要的特征做交叉,不能对所有特征做两两交叉。
Bilinear Cross(哈达玛乘积)
哈达玛方式,和上面累死,只不过把点乘那里改为了哈达玛乘积:
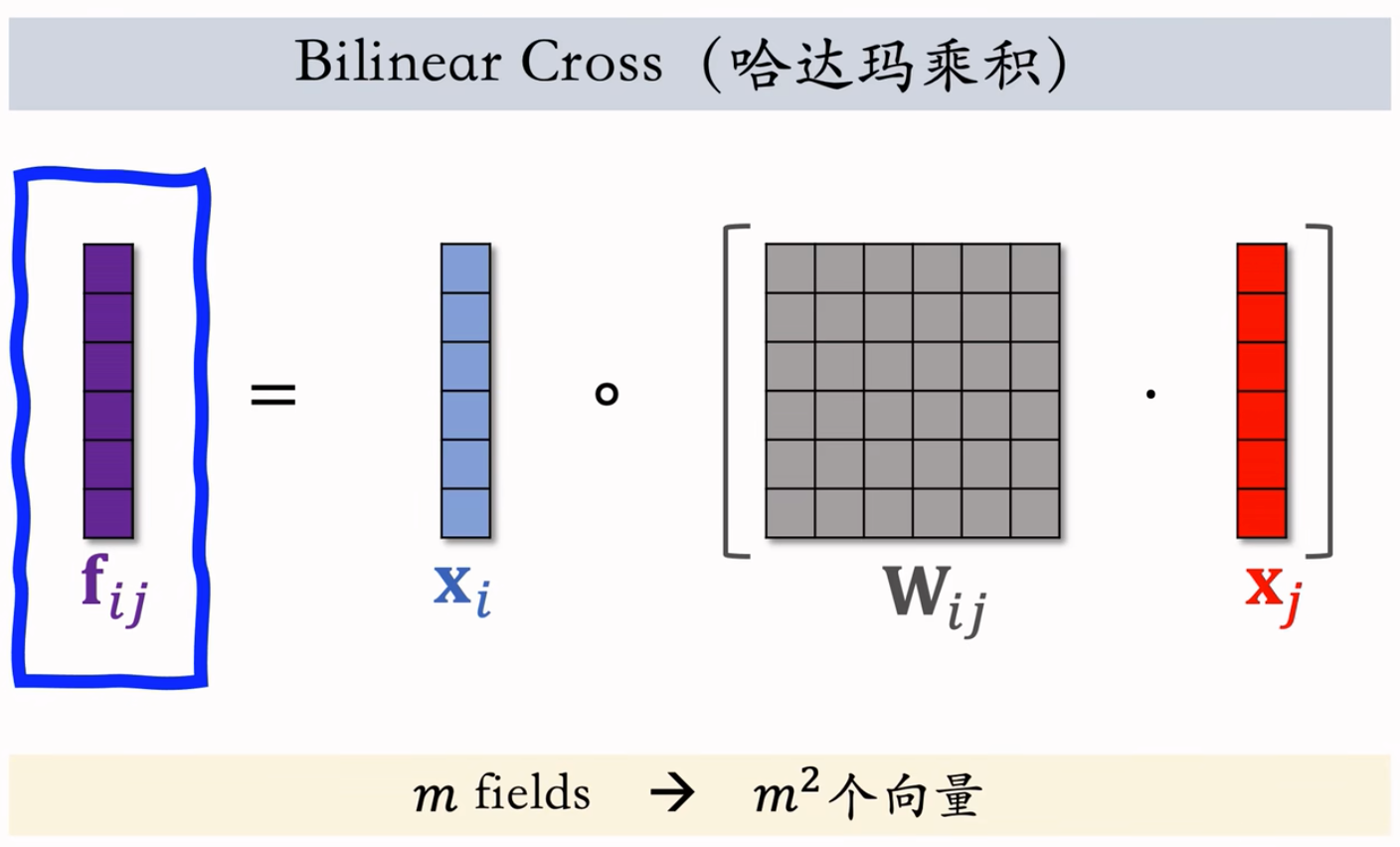
$m$ fields → $m^2$ 个向量
在实践中依然需要人工指定某些特征做交叉
小结
- SENet 对离散特征做 field-wise 加权
- Field 间特征交叉:
- 向量内积
- 哈达玛乘积
- Bilinear Cross
FiBiNet
模型结构
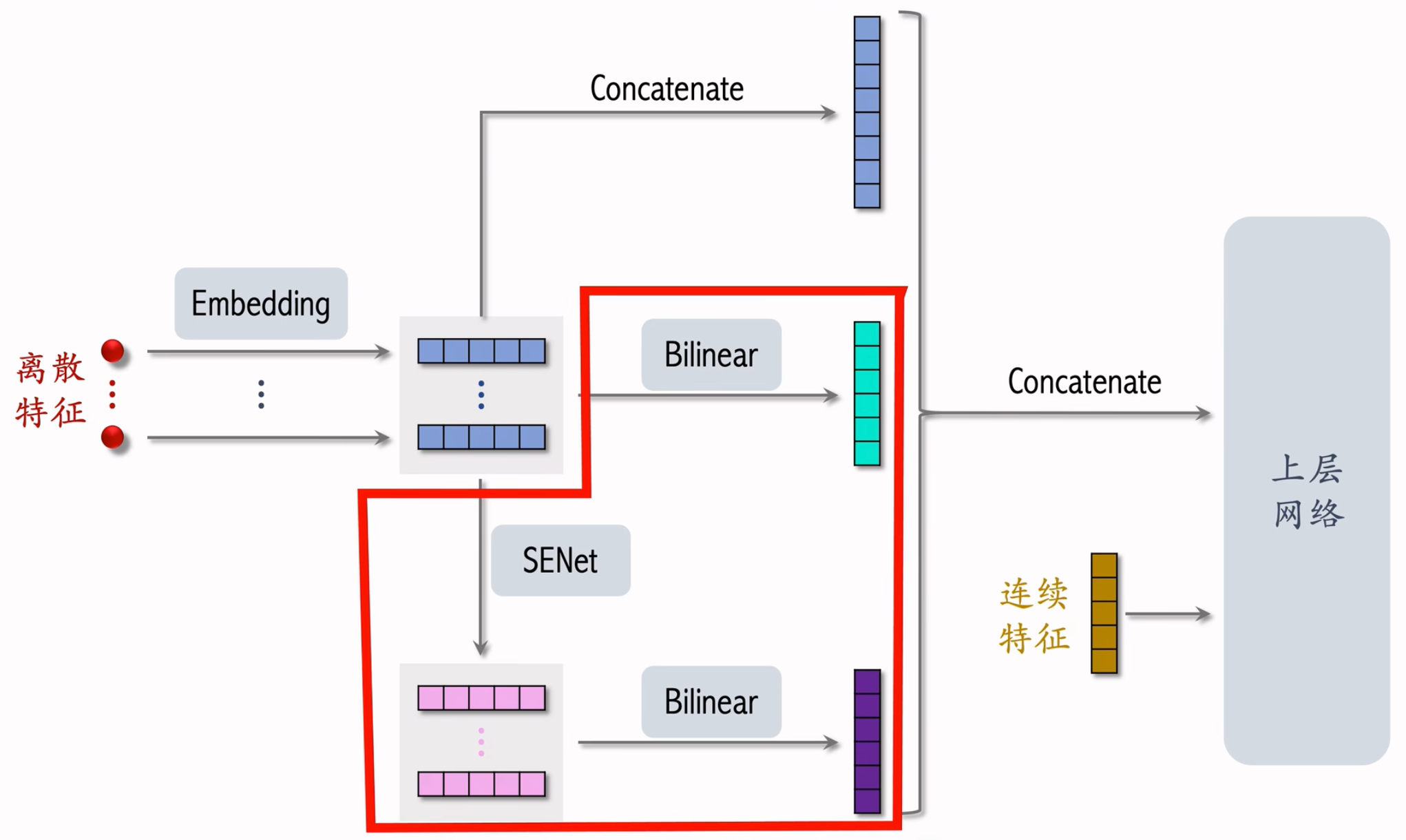
以前我们就直接把离散特征的 Embedding 拼接后再与连续特征拼接
FiBiNet 多做了一些工作
- 对离散特征的 Embedding 做 Bilinear Cross,得到交叉特征并拼接为 1 个向量
- 用 SENet 对 Embedding 做加权,再对这些向量做 Biliner Cross,得到交叉特征并拼接为 1 个向量。王老师个人认为这里的两条路径中,下面那条SENet -> Biliner Cross 多余了,小红书没有用,而是直接做了拼接。
小红书借鉴了 FiBiNet
- SENet 和 Bilinear Cross 在精排模型上确实有效
- 模型结构以及 Bilinear Cross 的实现都与原文区别很大
Last N
User Last N Modeling
用户行为序列简称为 LastN,即用户最后交互的 $n$ 个物品,LastN 可以反映用户对什么样的物品感兴趣。
适用于召回双塔模型、粗排三塔模型、精排模型,都可以用Last N。很有效!用于召回和排序,指标都会大涨!
本节课后面重点关注 用户特征 中的 LastN 行为序列。Last N记录是用户最近交互过的N个物品的ID。
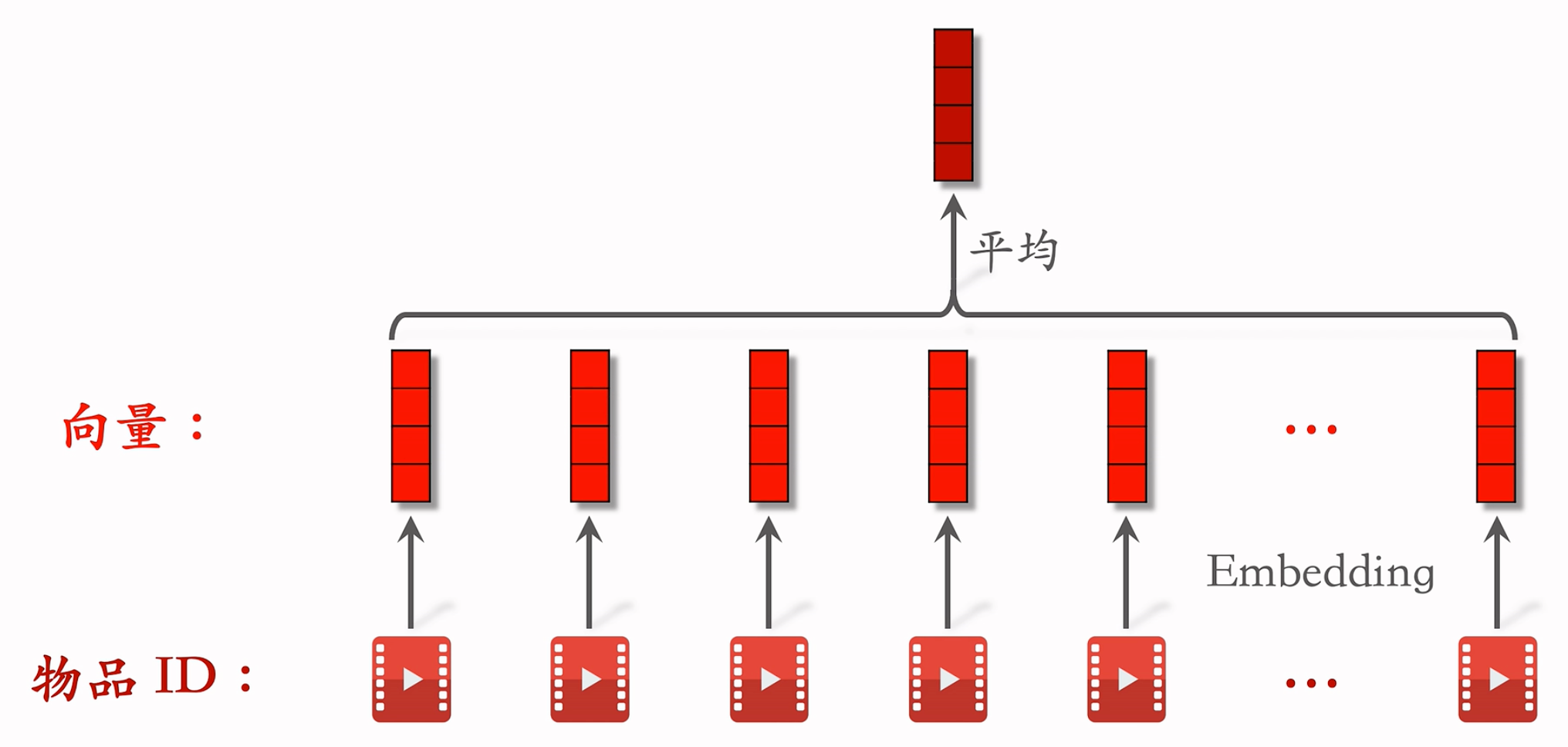
LastN 特征
- LastN:用户最近的 $n$ 次交互(点击、点赞等)的物品 ID
- 对 LastN 物品 ID 做 embedding,得到 $n$ 个向量
- 把 $n$ 个向量取平均,作为用户的一种特征/
- 适用于召回双塔模型、粗排三塔模型、精排模型
参考文献:Covington, Adams, and Sargin. Deep neural networks for YouTube recommendations. In ACM Conference on Recommender Systems, 2016.
小红书召回实践
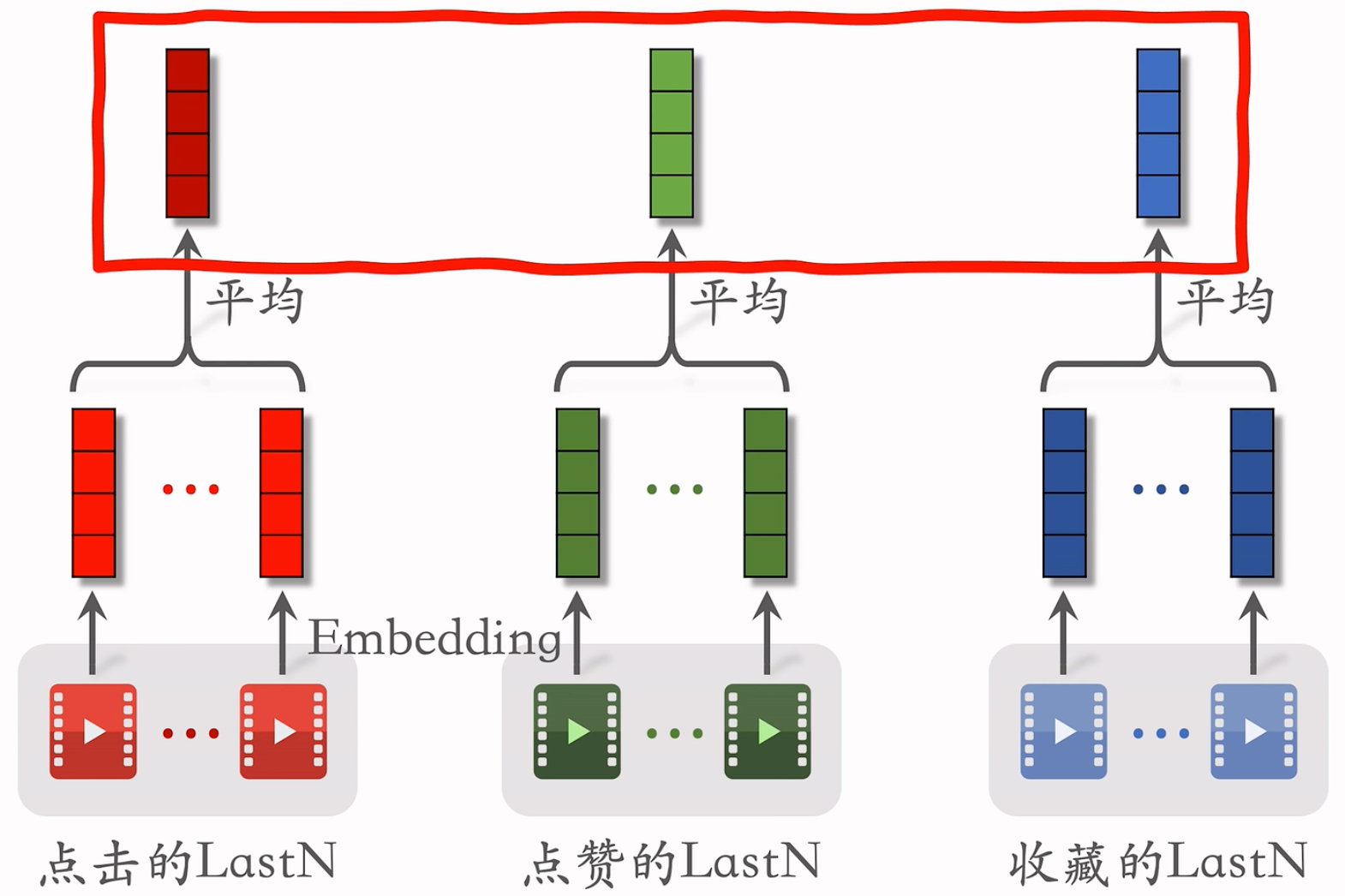
- 取平均是早期的用法,现在也很常用,效果不错。现在更多的是用 Attention,效果更好,计算量更大。
- 上面得到的多个向量拼接起来,作为一种用户特征,传到召回或排序模型中。
- 实际用Last N的时候,Embedding 不只有物品 ID,还会有物品类别等特征,把ID Embedding和其他的Em bedding拼在一起,效果更好。
DIN Model(Deep Interest Network)
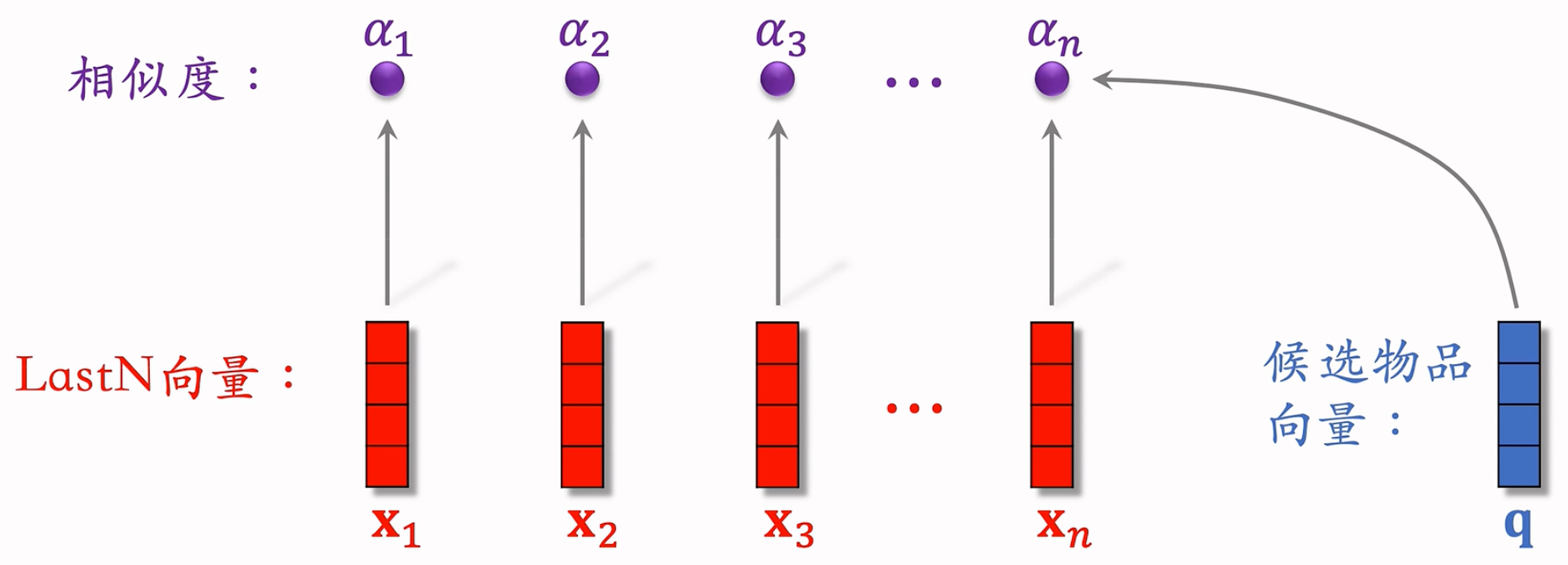
DIN 模型
- DIN 用加权平均代替平均,即注意力机制(attention)
- 权重:候选物品与用户 LastN 物品的相似度。哪个Last N和候选物品更相似,它的权重就越高。
参考文献:Zhou et al. Deep interest network for click-through rate prediction. In KDD, 2018.
计算过程:
候选物品:例如粗排选出了 500 个物品,那这 500 个就是精排的候选物品
计算相似度的方法很多,如 内积 和 余弦相似度 等
DIN 模型总结
- 计算相似度,可能用个cos之类的东西。每个Last N中的向量,都和q单独算一个。
- 相乘再相加:
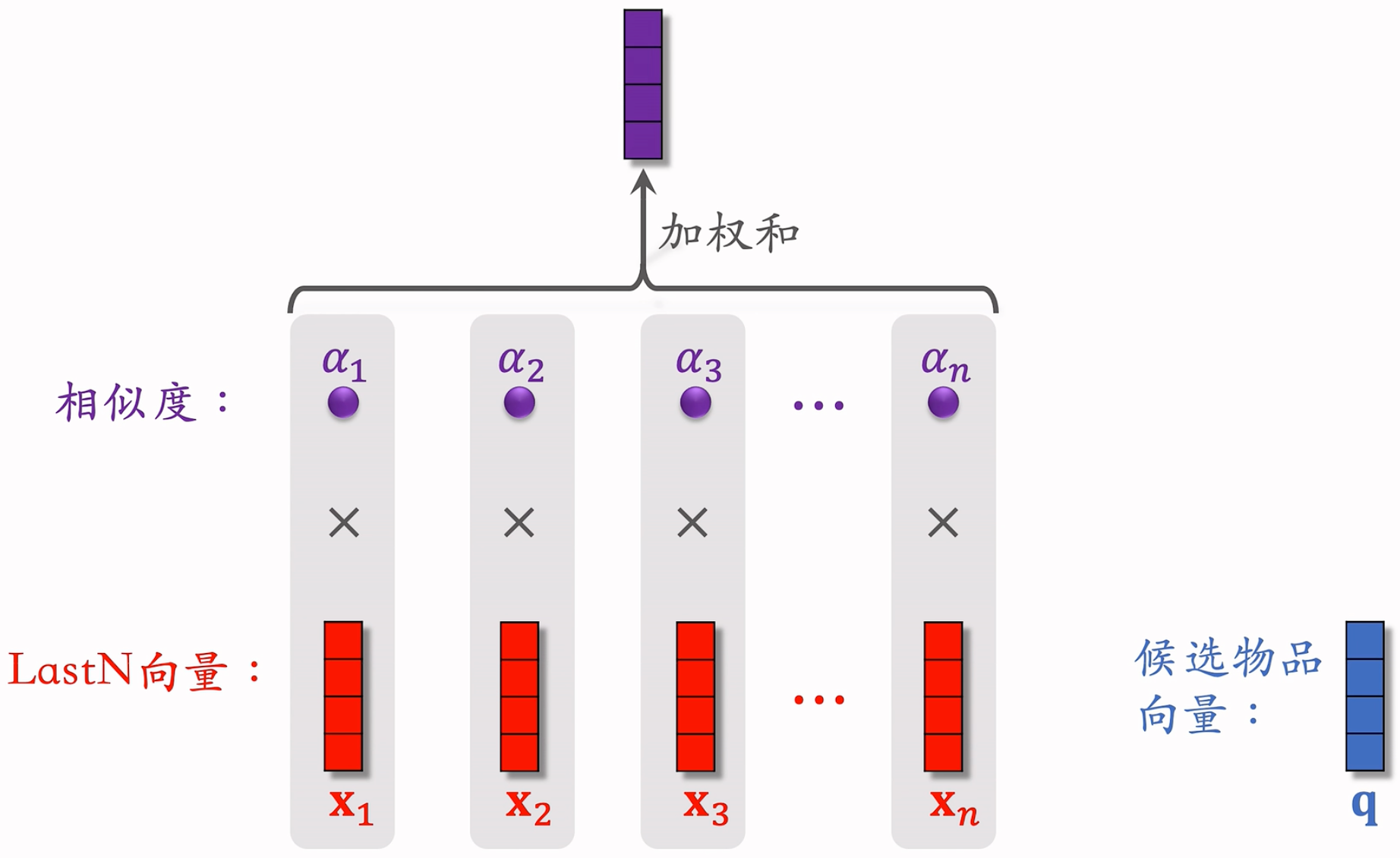
总结
- 对于某候选物品,计算它与用户 LastN 物品的相似度
- 以相似度为权重,求用户 LastN 物品向量的加权和,结果是一个向量
- 把得到的向量作为一种用户特征,输入排序模型,预估(用户,候选物品)的点击率、点赞率等指标
- 本质是注意力机制(attention)
注意力机制:
可以和Transformer的q, k, v对应上的昂!
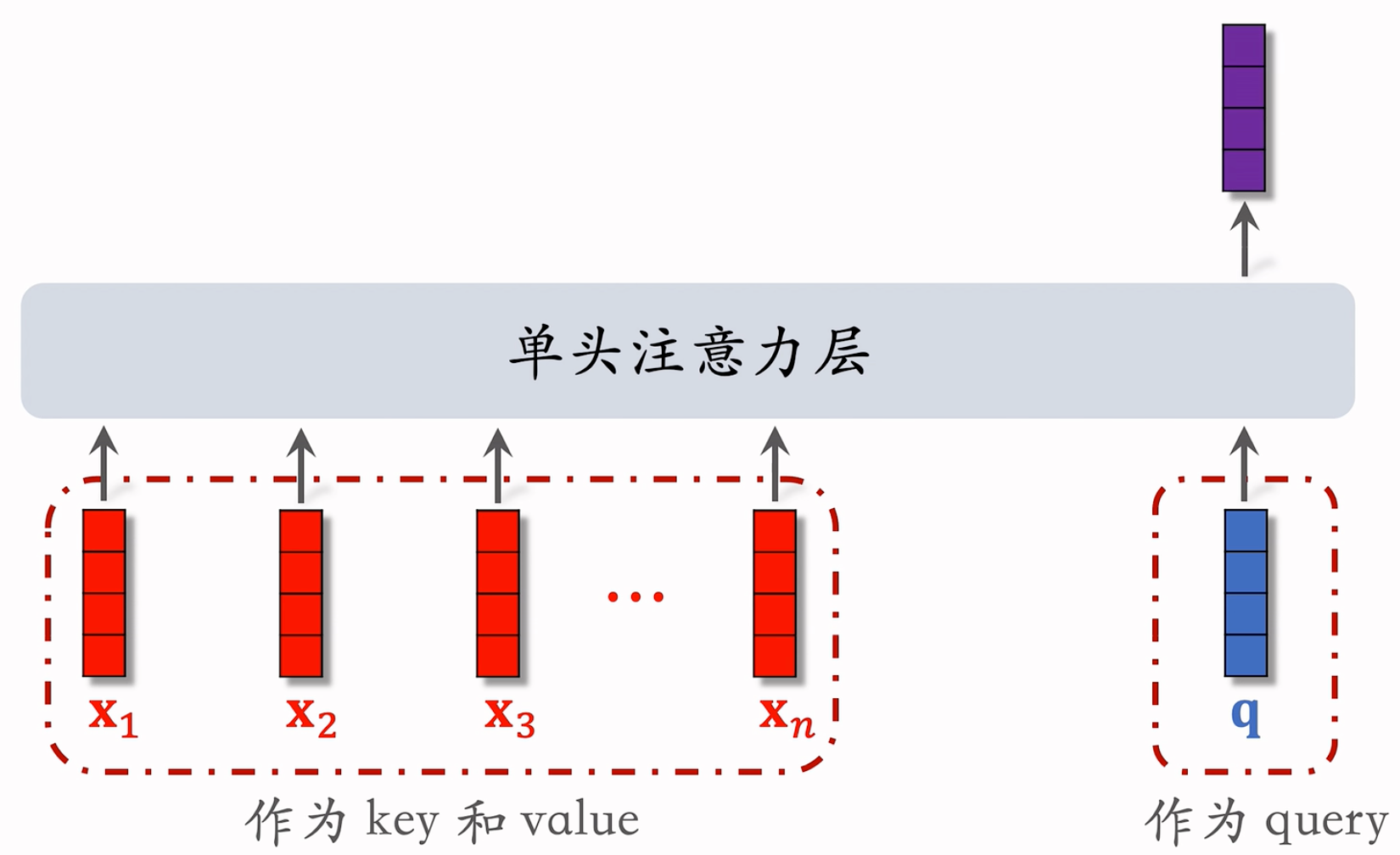
简单平均 v.s. 注意力机制:
- 简单平均 和 注意力机制 都适用于精排模型
- 简单平均适用于双塔模型、三塔模型
- 简单平均只需要用到 LastN,属于用户自身的特征,与候选物品无关
- 把 LastN 向量的平均作为用户塔的输入
- 注意力机制不适用于双塔模型、三塔模型
- 注意力机制 需要用到 LastN + 候选物品
- 用户塔看不到候选物品,不能把 注意力机制 用在用户塔
- 它是作为用户特征的,所以只会出现在用户这边。用双塔也就为了user_emb和item_emb,放到item tower没法跟user_tower的lastN做交叉。感觉双塔/三塔的后期融合,就杜绝了user和item在特征早期,做交叉/注意力机制的可能性。
SIM Model(Search-based User Interest Modeling)
SIM 模型的主要目的是保留用户的长期兴趣。
DIN 模型
- 计算用户 LastN 向量的加权平均
- 权重是候选物品与 LastN 物品的相似度
DIN 模型的缺点
- 注意力层的计算量 正比于 $n$(用户行为序列的长度)
- 只能记录最近几百个物品,否则计算量太大
- 缺点:关注短期兴趣,遗忘长期兴趣。王老师的同事做过实验,增长记录的行为序列,可以显著提升推荐系统的所有指标,但增加的计算量太大了
参考文献:Zhou et al. Deep interest network for click-through rate prediction. In KDD, 2018.
如何改进 DIN?
- 目标:保留用户长期行为序列($n$ 很大),而且计算量不会过大
- 改进 DIN:
- DIN 对 LastN 向量做加权平均,权重是相似度
- 如果某 LastN 物品与候选物品差异很大,则权重接近零
- 快速排除掉与候选物品无关的 LastN 物品,降低注意力层的计算量
SIM模型:
- 保留用户长期行为记录,$n$ 的大小可以是几千
- 对于每个候选物品,在用户 LastN 记录中做快速查找,找到 $k$ 个相似物品。(N = 1000,k = 100,从最近的1000个交互中,快速找到最相关的100个)
- 把 LastN 变成 TopK,然后输入到注意力层,k很小!就很厉害!
- SIM 模型减小计算量(从 $n$ 降到 $k$)
参考文献:Qi et al. Search-based User Interest Modeling with Lifelong Sequential Behavior Data for Click-Through Rate Prediction. In CIKM, 2020.
SIM步骤
第一步:查找
- 方法一:Hard Search —— 根据规则做筛选。
- 根据候选物品的类目,保留 LastN 物品中类目相同的
- 简单,快速,无需训练
- 方法二:Soft Search
- 把物品做 embedding,变成向量
- 把候选物品向量作为 query,做 $k$ 近邻查找,保留 LastN 物品中最接近的 $k$ 个
- 论文表明:Soft效果更好,AOC更高。编程实现更复杂,计算量也更高。
- 也要看基建,如果基建不行,Hard就可以了。
- 方法一:Hard Search —— 根据规则做筛选。
第二步:注意力机制
和DIM其实结构上没有什么大的不同。
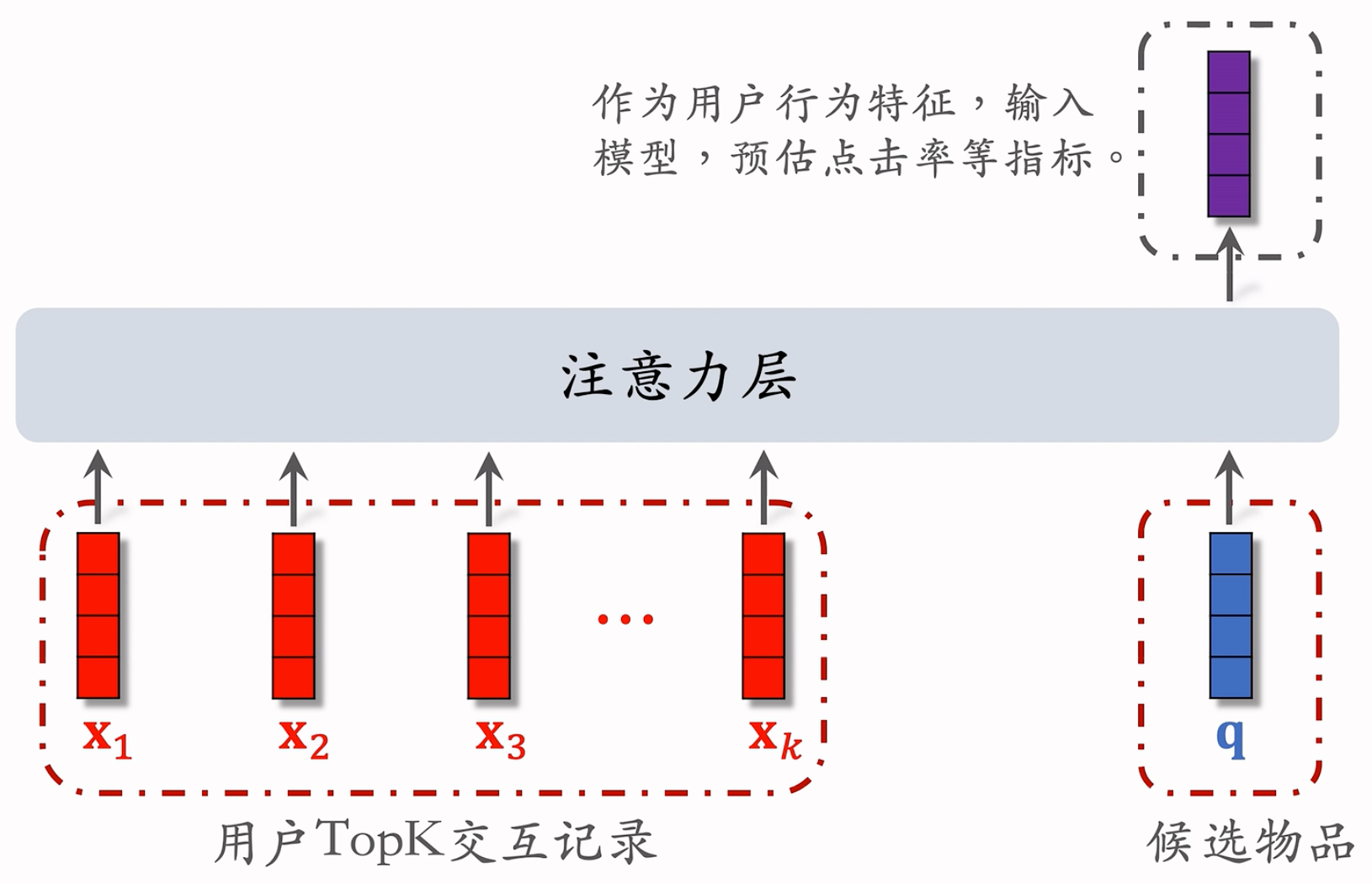
Top N变成Top K了哈
Trick:使用时间信息
- 用户与某个 LastN 物品的交互时刻距今为 $\delta$
- 对 $\delta$ 做离散化,再做 embedding,变成向量 $\bold{d}$ ,例如把时间离散为 1 天内、7 天内、30 天内、一年、一年以上。
- 把两个向量做 concatenation,表征一个 LastN 物品
- 向量 $\bold{x}$ 是物品 embedding
- 向量 $\bold{d}$ 是时间的 embedding
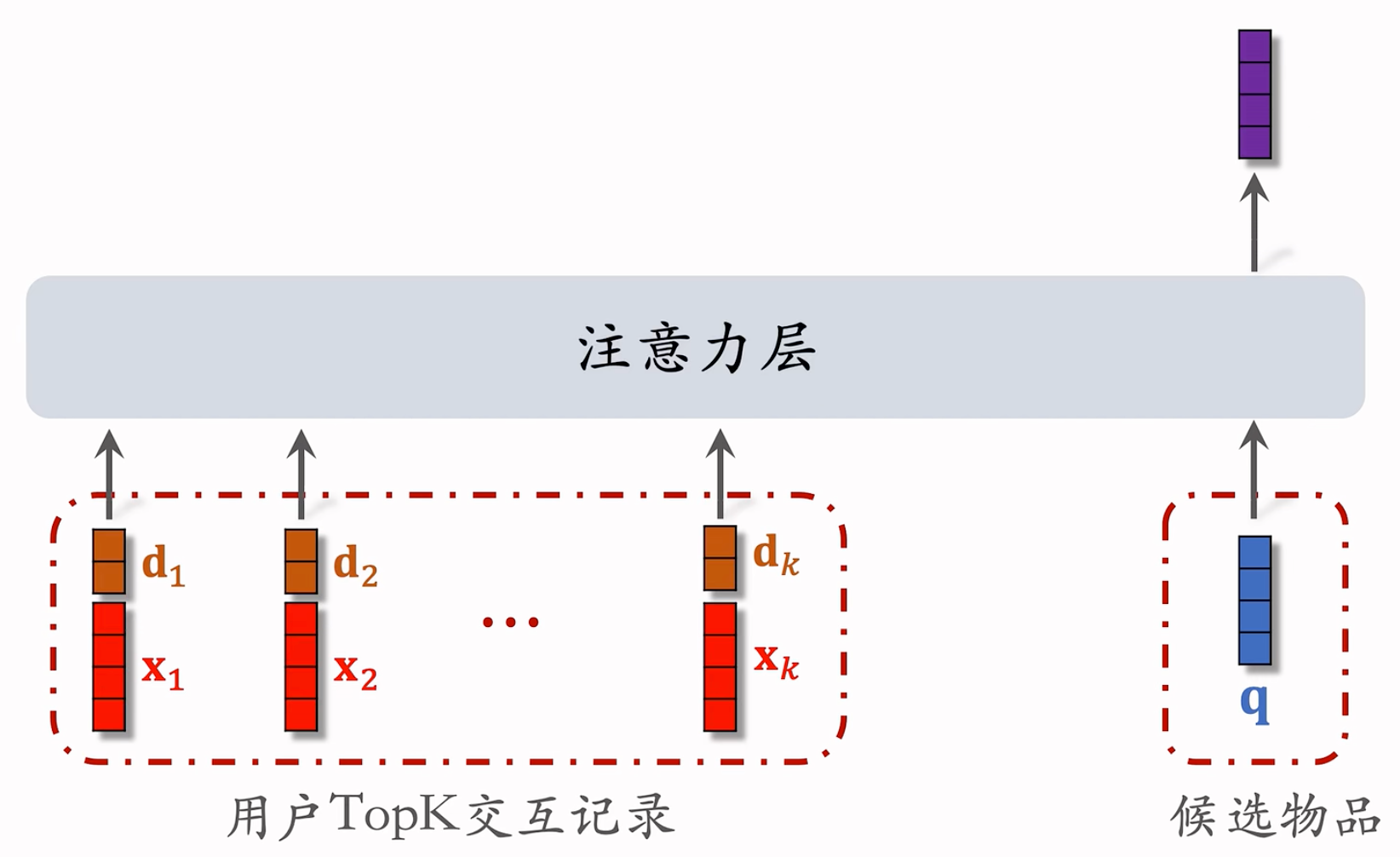
为什么SIM使用时间信息?
DIN 的序列短,记录用户近期行为
SIM 的序列长,记录用户长期行为
时间越久远,重要性越低
论文表明:使用时间信息可以带来显著的提升。
结论:
- 长序列(长期兴趣)优于短序列(近期兴趣)
- 注意力机制优于简单平均
- Soft search 还是 hard search?取决于工程基建
- 使用时间信息有提升
Ideas
- 感觉就是Top n -> Top k,多加了一层漏斗哈哈哈哈,别的没啥区别。
- 看到弹幕有人说,这个时间序列加上去,就和大模型里面,加上了Positional Embedding一样,这里的Position就是距离当前时间的位置,妙!新的思考方式,时空都可以抽象为Positional Embedding啊!
Re-ranking
Diversity in recommendation systems
多样性:推荐给用户的物品两两间不相似,则说明推荐有多样性。
物品相似度的度量
- 相似性的度量
- 基于物品属性标签:类目、品牌、关键词……
- 基于物品向量表征
- 用召回的双塔模型学到的物品向量(不好)
- 基于内容的向量表征(好),用CV/NLP模型,提取文字/图片的特征向量。
- 相似性的度量
基于物品属性标签 :
- 物品属性标签:类目、品牌、关键词……,标签通常是通过 CV 或 NLP 算法通过图文推算的,不一定准确。
- 根据 一级类目、二级类目、品牌 计算相似度
- 物品 $i$:美妆、彩妆、香奈儿
- 物品 $j$:美妆、香水、香奈儿
- 相似度:$\rm sim_1(i,j)=1,\rm sim_2(i,j)=0,\rm sim_3(i,j)=1$
- 加权和,得到相似度总分,权重根据经验设置。
双塔模型的物品向量表征:
结构:
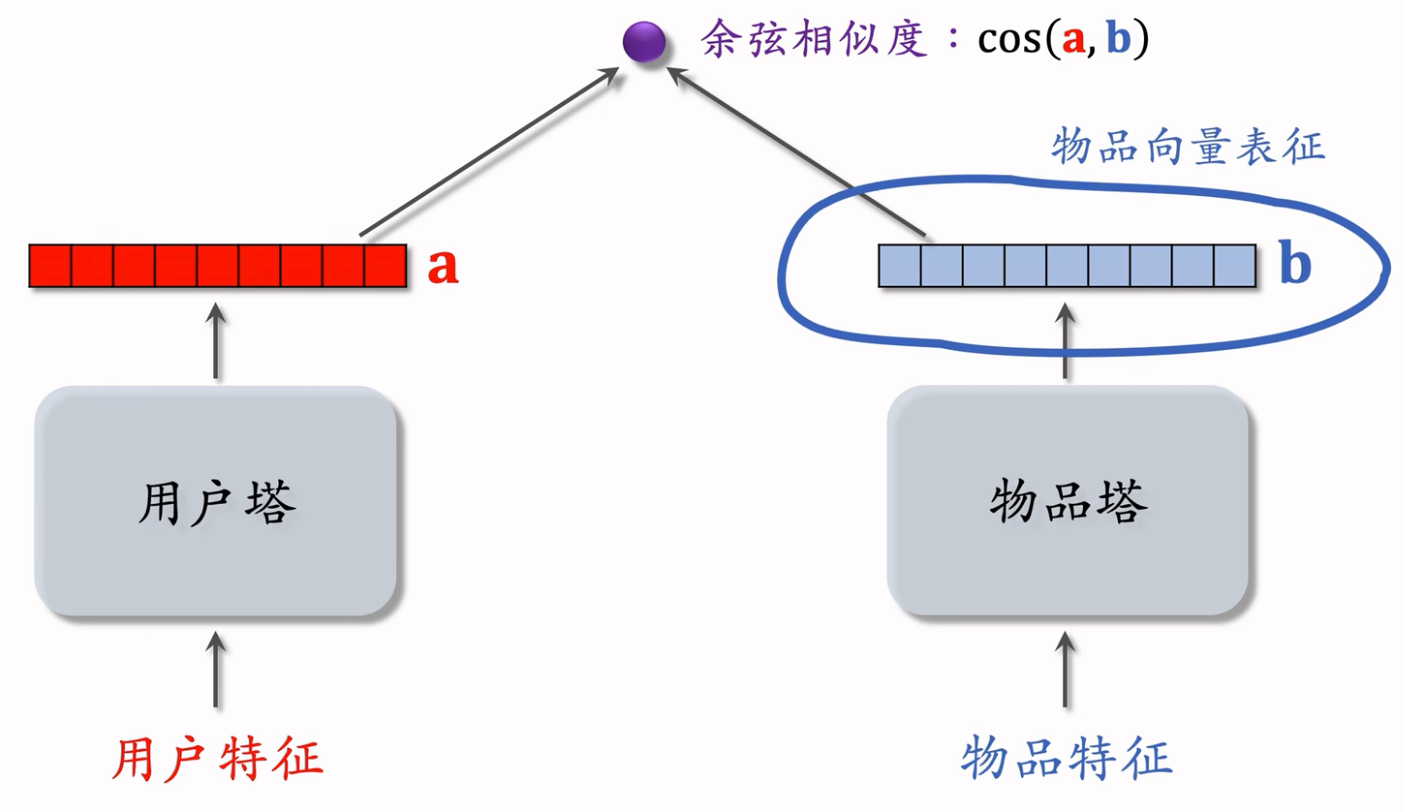
多样性问题上,我们只需要物品塔的输出。因为我们是对于物品的相似度做判别。如果相似,则物品向量表征的内积/余弦相似度比较大。
可以将物品塔的表征用在多样性问题上!但是!效果不太好。原因:
- 推荐系统的头部效应明显,新物品和长尾物品的曝光少。
- 双塔模型学不好 新物品 和 长尾物品 的向量表征。
基于图文内容的物品表征:
最好的办法!以小红书的笔记为例子,用CNN提取图片的向量,用Bert提取文字的特征拿到另外一个向量。这俩拼起来,就是图文笔记的表征。
Bert/CNN怎么训练呢?公开的对于小红书效果不好,如果用内部的数据做训练,还要人工标注,比较麻烦。
CLIP是当前公认最有效的预训练方法。
- 思想: 对于图片,文本二元组,预测图文是否匹配。
- 优势:无需人工标注。小红书的笔记天然包含图片 + 文字,大部分笔记图文相关
- 做预训练时:同一篇笔记的图文 作为正样本,它们的向量应该高度相似;来自不同笔记的图文作为负样本。
参考文献:Radford et al. Learning transferable visual models from natural language supervision. In ICML, 2021.
基于图文内容的物品表征
- 一个 batch 内有 $m$ 对正样本
- 一张图片和 $m-1$ 条文本组成负样本,这个 batch 内一共有 $m(m-1)$ 对负样本。
提升多样性的方法:
粗排和精排用多目标模型对物品做 pointwise打分,就打分,不考虑物品间的关联。
对于物品 $i$,模型输出点击率、交互率的预估,融合成分数 $reward _i$
$reward _i$ 表示用户对物品 $i$ 的兴趣,即物品本身对用户的价值。
粗排/精排:给定 $n$ 个候选物品,排序模型打分 ${\rm{reward}} _i,…,{\rm{reward}} _n$。

后处理:从 $n$ 个候选物品中选出 $k$ 个,既要它们的总分高,也需要它们有多样性。
增加多样性可以显著提升推荐系统指标(尤其是时长、留存率),所以工业界在后处理阶段,都是使用多样性算法。
精排的后处理通常被称为 — 重排,它决定n个物品中,哪k个曝光,以及展示给用户的顺序。粗排的后处理往往被大家忽视,也需要多样性算法,而不是简单的从几千个物品中选reward最高的几百个,也能提升业务指标!优化粗排之后在小红书获得了很大的收益,有意义的!
Maximal Marginal Relevance (MMR)
最早被用到搜索排序,然后才被用在推荐排序,沿用了MMR这个名字
多样性
- 精排给 $n$ 个候选物品打分,融合之后的分数为 $\rm{reward} _i,…,\rm{reward} _n$,n的大小一般是几百
- 把第 $i$ 和 $j$ 个物品的相似度记作 $\rm sim(i,j)$
- 重排:从 $n$ 个物品中选出 $k$ 个,既要有高精排分数,也要有多样性
计算集合 ${\mathcal{R}}$ 中每个物品 $i$ 的 Marginal Relevance 分数: ${{\mathrm{MR}_{i}}}={{\theta\cdot\mathrm{reward}_{i}-(1-\theta)\cdot\max_{j\in {\mathcal{S}}}{sim}(i,j)}}${#
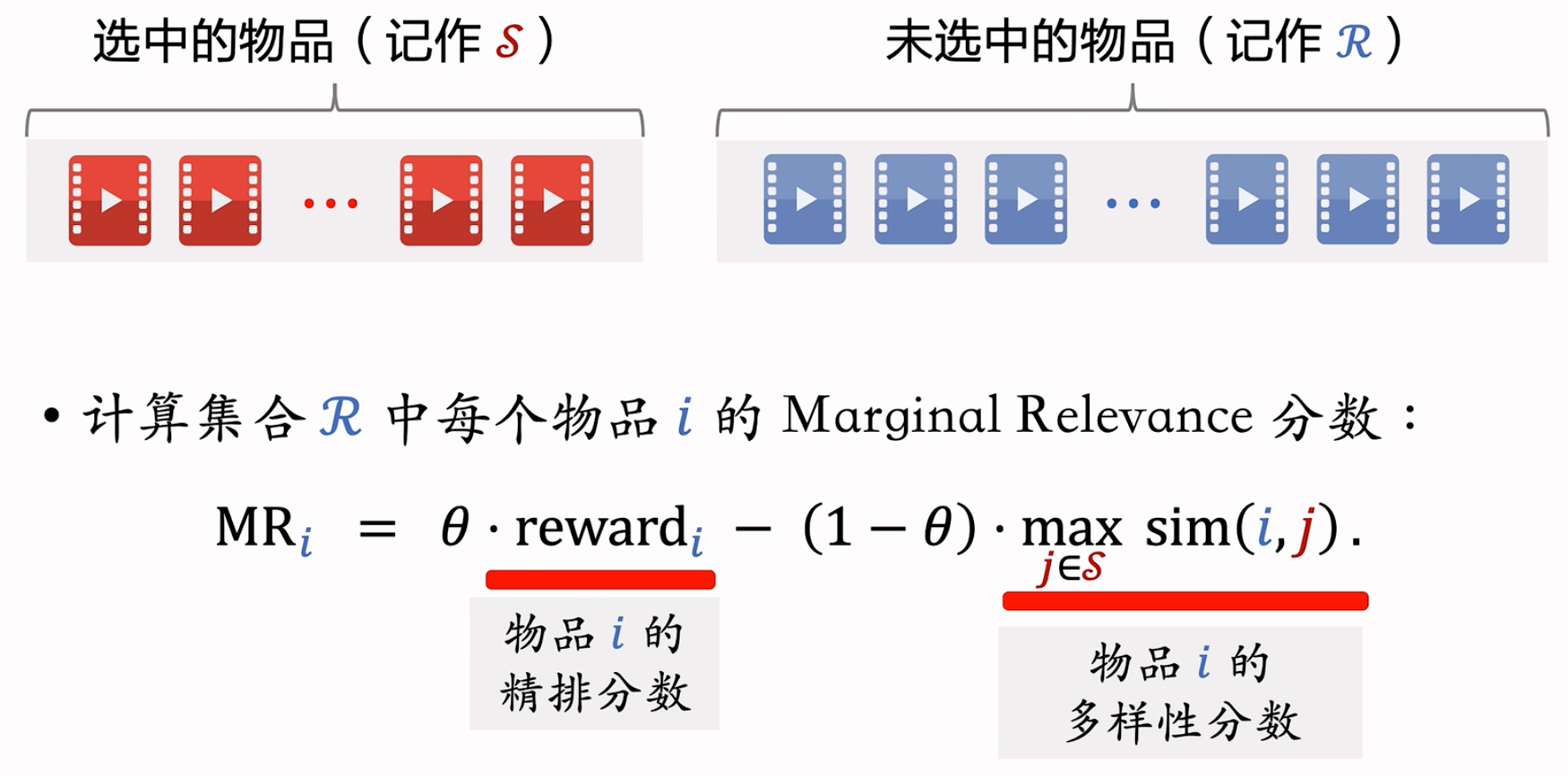
- $reward_i$:物品 $i$ 的精排分数
- $\max_{j\in \mathcal{S}} sim(i,j)$:物品 $i$ 的多样性分数
- 物品 $i$ 尚未选中,而物品 $j\in \mathcal{S}$ 都是已选中物品
- 若物品 $i$ 与已选中的某个物品 $j$ 相似度比较大,则起到抑制作用
- theta属于0,1之间的参数,平衡物品的价值和多样性。theta越大,则reward更重要,越小,则多样性更重要。
Maximal Marginal Relevance (MMR): ${\rm argmax}_{i\in {\mathcal{R}}} {\rm MR}_i$
- 每一轮从集合 $\mathcal{R}$ 中选择 $ {\rm MR}$ 分数最高的物品 $i$,然后将其移入集合 $\mathcal{S}$
概括 MMR 算法流程:
- 初始化:已选中的物品 ${\mathcal{S}}$ 初始化为空集,未选中的物品 ${\mathcal{R}}$ 初始化为全集 ${ 1,…,n}$
- 选择精排分数 $\rm{reward} _i$ 最高的物品,从集合 ${\mathcal{R}}$ 移到 ${\mathcal{S}}$
- 做 $k-1$ 轮循环:
- 计算集合 ${\mathcal{R}}$ 中所有物品的分数 $<!–swig4–>}$
- 选出分数最高的物品,将其从 ${\mathcal{R}}$ 移到 ${\mathcal{S}}$
滑动窗口:
MMR: $argmax_{i\in {\mathcal{R}}} \{ {{\theta\cdot\mathrm{reward}_{i}-(1-\theta)\cdot\max_{j\in {\mathcal{S}}}sim(i,j)}}\}$ {#
- 缺点:已选中的物品越多(即集合 ${\mathcal{S}}$ 越大),越难找出物品 $i\in{\mathcal{R}}$,使得 $i$ 与 ${\mathcal{S}}$ 中的物品都不相似。
- 设 $\rm sim$ 的取值范围是 [0, 1]。当 ${\mathcal{S}}$ 很大时,多样性分数 $\max_{j\in \mathcal{S}}\rm sim(i,j)$ 总是约等于 1,导致 MMR 算法失效
解决方案:设置一个滑动窗口 ${\mathcal{W}}$,比如最近选中的 10 个物品,用 ${\mathcal{W}}$ 代替 MMR 公式中的 ${\mathcal{S}}$
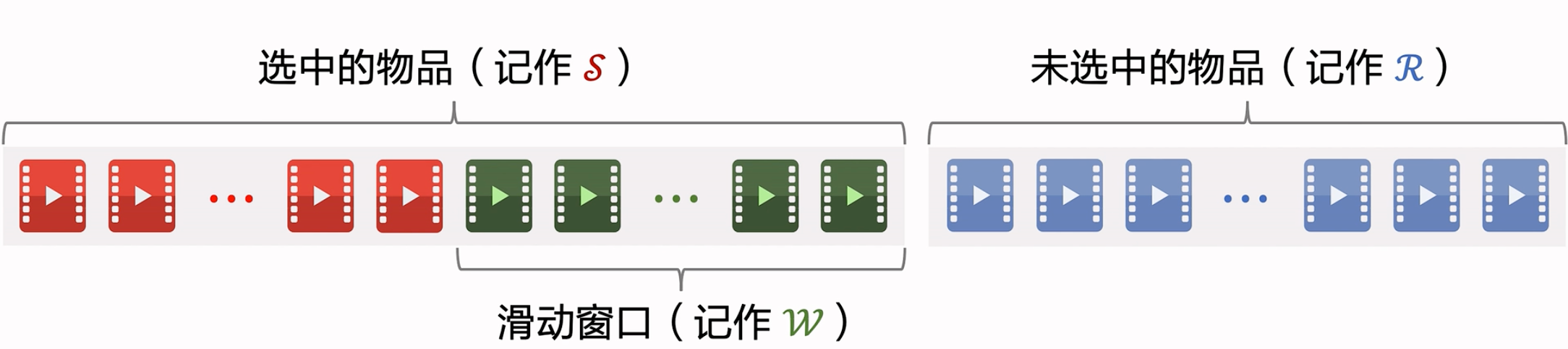
标准 MMR:$argmax_{i\in {\mathcal{R}}} \{ {{\theta\cdot\mathrm{reward}_{i}-(1-\theta)\cdot\max_{j\in {\mathcal{S}}}sim(i,j)}}\}$ {#
用滑动窗口:$argmax_{i\in {\mathcal{R}}} \{ {{\theta\cdot\mathrm{reward}_{i}-(1-\theta)\cdot\max_{j\in {\mathcal{W}}}sim(i,j)}}\}$ {#
用滑动窗口的可解释性:给用户曝光的连续物品应该不相似,但没必要最新的物品和 30 个之前的物品还不相似。
没必要嘛,看到30个之后,早都忘了之前的了。核心想法:远的可以相似,但是近的不行,要有较大的差异。否则用户可以感知到多样性不好。
总结:
- MMR 使用在精排的后处理(重排)阶段
- 根据精排分数和多样性分数给候选物品排序
- MMR 决定了物品的最终曝光顺序
- 实际应用中通常带滑动窗口,这样比标准 MMR 效果更好
Re-ranking Rules
推荐系统有很多业务规则,比如不能连续出多篇某种类型的物品、某两种类型的物品笔记间隔多少。这些业务规则应用在重排阶段,可以与 MMR、DPP 等多样性算法相结合。
简介
工业界的推荐系统一般有很多业务规则,这些规则通常是为了保护用户体验,做重排时这些规则必须被满足
下面举例重排中的部分规则,以及这些规则与 MMR 相结合
规则的优先级高于多样性算法
重排的规则:
规则:最多连续出现 $k$ 篇某种笔记
- 小红书推荐系统的物品分为图文笔记、视频笔记
- 最多连续出现 $k=5$ 篇图文笔记,最多连续出现 $k=5$ 篇视频笔记
- 如果排 $i$ 到 $i+4$ 的全都是图文笔记,那么排在 $i+5$ 的必须是视频笔记
规则:每 $k$ 篇笔记最多出现 1 篇某种笔记
- 运营推广笔记的精排分会乘以大于 1 的系数(boost),帮助笔记获得更多曝光
- 为了防止 boost 影响体验,限制每 $k=9$ 篇笔记最多出现 1 篇运营推广笔记
- 如果排第 $i$ 位的是运营推广笔记,那么排 $i+1$ 到 $i+8$ 的不能是运营推广笔记
规则:前 $t$ 篇笔记最多出现 $k$ 篇某种笔记
- 排名前 $t$ 篇笔记最容易被看到,对用户体验最重要(小红书的 top 4 为首屏)
- 小红书推荐系统有带电商卡片的笔记,过多可能会影响体验
- 前 $t=1$ 篇笔记最多出现 $k=0$ 篇带电商卡片的笔记。即排名第一的笔记,不能是电商推广
- 前 $t=4$ 篇笔记最多出现 $k=1$ 篇带电商卡片的笔记
注:不是小红书的真实数据
MMR + 重排规则
- MMR 每一轮选出一个物品,重排要结合 MMR 与规则,在满足规则的前提下最大化 MR。
- 每一轮要先用规则,从备选集合$R$中,排除掉部分物品,得到子集$R’$
- 将MMR公式中的$R$替换为子集$R’$,选中的物品符合规则。
- 很容易的集合,公式都不变,就换个选物品的集合 -> 合规的子集就可以了!
DPP(Determinantal Point Process)
行列式点过程 (determinantal point process, DPP) 是一种经典的机器学习方法,在 1970’s 年代提出,在 2000 年之后有快速的发展。DPP 是目前推荐系统重排多样性公认的最好方法。
DPP 的数学比较复杂,这节课先介绍数学基础,下节课再介绍它在推荐系统的应用。这节课的内容主要是超平行体、超平行体的体积、行列式与体积的关系。
参考文献: Chen et al. Fast greedy map inference for determinantal point process to improve recommendation diversity. In NIPS, 2018.
Math Basics
背景:线性代数
DPP:行列式点过程
DPP 的目标是从一个集合中选出尽量多样化的物品,契合重排的目标
它是目前推荐系统领域公认的最好多样性算法
超平形体
二维空间
平行四边形
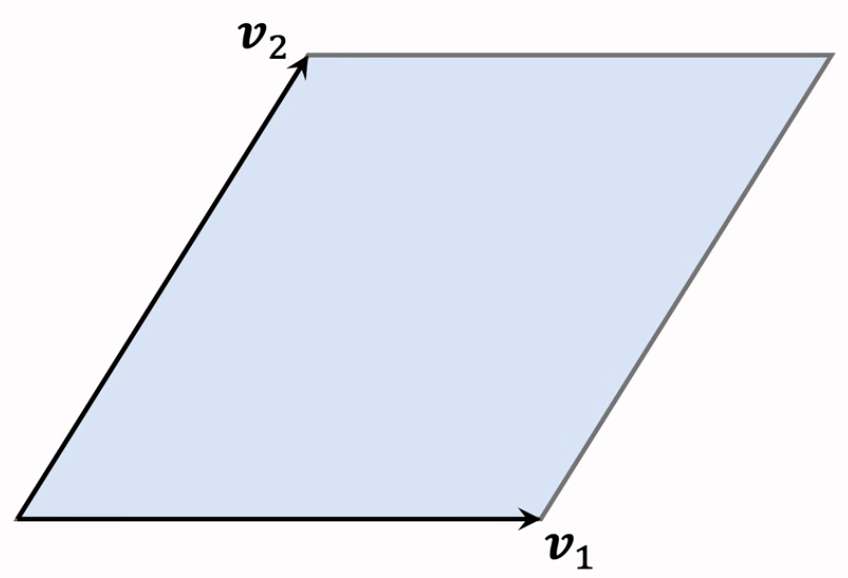
平行四边形中的任何一个点可以表示为:$x=\alpha_{1}v_{1}+\alpha_{2}v_{2}$
系数 $\alpha_{1}$ 和 $\alpha_{2}$ 取值范围是 [0,1]
三维空间
平行六面体
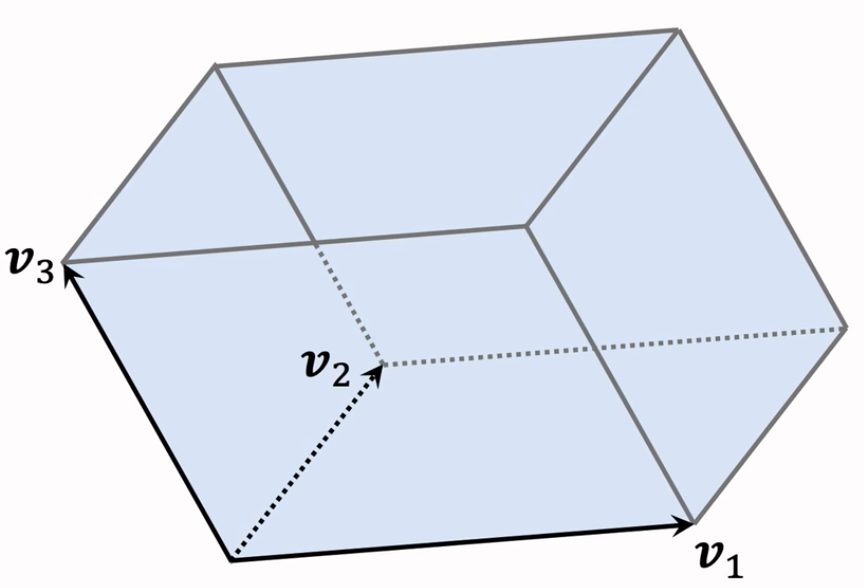
平行六面体中的任何一个点可以表示为:$x=\alpha_{1}v_{1}+\alpha_{2}v_{2}+\alpha_{3}v_{3}$
系数 $\alpha_{1},\alpha_{2},\alpha_{3}$ 取值范围是 [0,1]
超平形体的数学定义为:
- 一组向量 $v_{1},\cdots,v_{k}\in\mathbb{R}^{d}$ 可以确定一个 $k$ 维超平行体:${\mathcal{P}}(v_{1},\cdots,v_{k})={\alpha_{1}v_{1}+\cdots+\alpha_{k}v_{k}\mid0\leq\alpha_{1},\cdots,\alpha_{k}\leq1}$
- 要求 $k\leq d$,比如 $d=3$ 维空间中有 $k=2$ 维平行四边形
- 如果想让超平形体有意义,那么 $v_{1},\cdots,v_{k}$ 必须线性无关
- 如果 $v_{1},\cdots,v_{k}$ 线性相关,则体积 ${\rm vol} ({\mathcal{P}})=0$。(例:有 $k=3$ 个向量,落在一个平面上,则平行六面体的体积为 0)
面积/体积计算:
平行四边形:
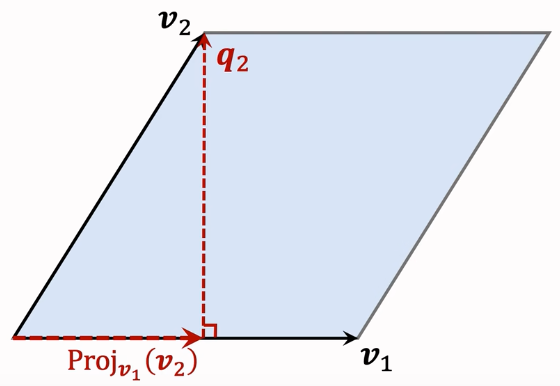
计算 $v_2$ 在 $v_1$ 上的投影: $\mathrm{Proj}{v{1}}(v_{2})={\frac{v_{1}^{T}v_{2}}{||v_{1}||{2}^{2}}}\cdot v{1}$ ,计算 $q_{2}=v_{2}-\mathrm{Proj}{v{1}}(v_{2})$ ,性质:底 $v_1$ 与高 $q_2$ 正交
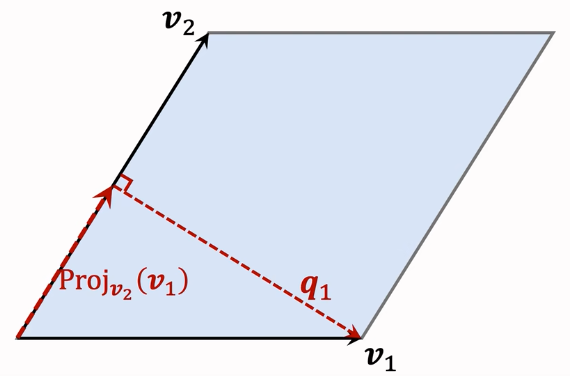
计算 $v_1$ 在 $v_2$ 上的投影: $\mathrm{Proj}{v{2}}(v_{1})={\frac{v_{1}^{T}v_{2}}{||v_{2}||{2}^{2}}}\cdot v{2}$ ,计算 $q_{1}=v_{1}-\mathrm{Proj}{v{2}}(v_{1})$ ,性质:底 $v_2$ 与高 $q_1$ 正交 。
平行六面体的体积
- 体积 = $底面积× ||高||_2$
- 平行四边形 $ {\mathcal{P}}(v_1,v_2)$ 是平行六面体 $ {\mathcal{P}}(v_1,v_2,v_3)$ 的底,就用上面讲的方法计算该平行四边形的面积。
- 高 $q_3$ 垂直于底 $ {\mathcal{P}}(v_1,v_2)$
如果固定向量 $v_1,v_2,v_3$ 的长度,体积何时最大化、最小化?
- 设 $v_1,v_2,v_3$ 都是单位向量
- 当三个向量正交时,平行六面体为正方体,体积最大化, $\rm vol=1$
- 当三个向量线性相关时,体积最小化,$\rm vol=0$
衡量物品的相似性
给定 $k$ 个物品,把它们表征为单位向量 $v_{1},\cdots,v_{k}\in\mathbb{R}^{d}$( $d\geq k$)
用超平行体的体积衡量物品的多样性,体积介于 0 和 1 之间
如果 $v_{1},\cdots,v_{k}$ 两两正交(多样性好),则体积最大化,$vol=1$,如果 $v_{1},\cdots,v_{k}$ 线性相关(多样性差),则体积最小化,$vol=0$
给定 $k$ 个物品,把它们表征为单位向量 $v_{1},\cdots,v_{k}\in\mathbb{R}^{d}$( $d\geq k$)
把它们作为矩阵 $V\in\mathbb{R}^{d\times k}$ 的列
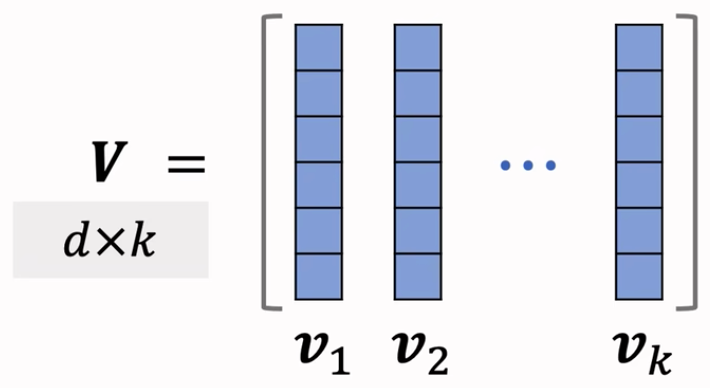
设 $d\geq k$
- 行列式与体积满足: $\operatorname*{det}(V^{T}V),=,\operatorname*{vol}(\mathcal{P}(v_{1},\cdots,v_{k}))^{2}$
- 即行列式和体积是等价的,最大化行列式等价于最大化体积。
- 因此,可以用行列式 $\operatorname*{det}(V^{T}V)$ 衡量向量 $v_{1},\cdots,v_{k}$ 的多样性
Diversity Algorithm
多样性问题
- 精排给 $n$ 个物品打分:$\rm{reward} _i,…,\rm{reward} _n$
- $n$ 个物品的向量表征:$v_{1},\cdots,v_{k}\in\mathbb{R}^{d}$
- 从 $n$ 个物品中选出 $k$ 个物品,组成集合 $\mathcal{S}$
- 价值大:分数之和 $\sum_{j\in\mathcal{S}} {\rm{reward}}_j$ 越大越好
- 多样性好:$\mathcal{S}$ 中 $k$ 个向量组成的超平形体 $\mathcal{P}(\mathcal{S})$ 的体积越大越好
DPP过程:
DPP 是一种传统的统计机器学习方法:$\operatorname{argmax}{\mathcal{S}:|{\mathcal{S}}|=k}\log\operatorname*{det}(V{\mathcal{S}}^{T},V_{\mathcal{S}})$
- 从集合 $\mathcal{ S}$ 中选出 $k$ 个
- 该公式严格来说叫 k-DPP
Hulu 的论文将 DPP 应用在推荐系统: $\begin{array}{l}{{argmax_{\mathcal{S:| \mathcal{S} |=k}}}}\end{array}\theta\cdot\left(\sum_{j\in \mathcal{S}}\mathrm{reward}_{j}\right)+(1-\theta)\cdot\log\operatorname*{det}(V_{\mathcal{ S}}^{T}\,V_{\mathcal{ S}})$ {#
- 前半部分计算集合中物品的价值
- 后半部分是行列式的对数,物品多样性越好,这部分越大
- Hulu 论文的主要贡献不是提出该公式,而是快速求解该公式
参考文献:Chen et al. Fast greedy map inference for determinantal point process to improve recommendation diversity. In NIPS, 2018.
DPP 是个组合优化问题,从集合 ${ 1,…,n}$ 中选出一个大小为 $k$ 的子集 $\mathcal{ S}$,精确 DPP 是不可能的,因为它是个 NP-hard 问题。
简单来讲,Hulu提出的算法,可以降低时间复杂度,通过矩阵运算的技巧。可以求出现有矩阵“加上一行,加上一列”,得到的结果,并且很快,不需要重新计算整个矩阵。在现有选择的物品(矩阵)上,再选择一个物品(矩阵上加一行一列),传统算法需要重新计算整个矩阵,但是Hulu提出的算法,能够在之前的运算结果上,能够快速算出新矩阵的近似准确值,从而快速得到结果。这种速度和时间复杂度上取得的提升,使DPP确实能够直接用在操作系统中。
详细算法过程可以回去看Wang老师的课程,或者精读论文和相关笔记。
DPP拓展
- 滑动窗口
- 用 S 表示已选中的物品,用 R 表示未选中的物品,DPP 的贪心算法求解: $\begin{array}{c}{{\mathrm{argmax_{i\in \mathcal{R}}}~\theta\cdot{\rm reward} }_{i}\ +\ (1-\theta)\cdot\log \mathrm{det}(\bold{ \textstyle{A}}_{\mathcal{ S}\cup\{i\}})}\end{array}$ {#
- 缺点:
- 随着集合 $\mathcal{ S}$ 增大,其中相似物品越来越多,物品向量会趋近线性相关
- 导致行列式 ${\rm det}(\bold{ \textstyle{A}}_{\mathcal{ S}})$ 会坍缩到零,对数趋于负无穷
- 贪心算法: $\begin{array}{c}{{\mathrm{argmax_{i\in \mathcal{R}}}~\theta\cdot{\rm reward} }_{i}\ +\ (1-\theta)\cdot\log \mathrm{det}(\bold{ \textstyle{A}}_{\mathcal{ S}\cup\{i\}})}\end{array}$ {#
- 滑动窗口: $\begin{array}{c}{{\mathrm{argmax_{i\in \mathcal{R}}}~\theta\cdot{\rm reward} }_{i}\ +\ (1-\theta)\cdot\log \mathrm{det}(\bold{ \textstyle{A}}_{\mathcal{ W}\cup\{i\}})}\end{array}$ {#
- 规则约束
- 贪心算法每轮从 $\mathcal{ R}$ 中选出一个物品:$\begin{array}{c}{{\mathrm{argmax_{i\in \mathcal{R}}}~\theta\cdot{\rm reward} }_{i}\ +\ (1-\theta)\cdot\log \mathrm{det}(\bold{ \textstyle{A}}_{\mathcal{ W}\cup\{i\}})}\end{array}$ {#
- 有很多规则约束,例如最多连续出 5 篇视频笔记(如果已经连续出了 5 篇视频笔记,下一篇必须是图文笔记)
- 用规则排除掉 $\mathcal{ R}$ 中的部分物品,得到子集 $\mathcal{ R}’$,然后求解:$\begin{array}{c}{{\mathrm{argmax_{i\in \mathcal{R'}}}~\theta\cdot{\rm reward} }_{i}\ +\ (1-\theta)\cdot\log \mathrm{det}(\bold{ \textstyle{A}}_{\mathcal{ W}\cup\{i\}})}\end{array}$ {#
- 这一部分的操作,感觉和上面的做法都是很一样的,这种思想直接平迁到了DPP。
- 滑动窗口
Item Cold Start
很少有 UGC(User Generated Content) 能让冷启动达到天花板。
Optimization goals & evaluation indicators
物品冷启动
- 小红书上用户新发布的笔记
- B站上用户新上传的视频
- 今日头条上作者新发布的文章
此处主要考虑 UGC(User Generated Content) 的物品冷启动
- 与 UGC 相反的是 PGC(Platform Generated Content),例如网飞、腾讯视频
- UGC 冷启比 PGC 更难,因为用户上传的内容良莠不齐,而且量大
思考:为什么要特殊对待新笔记?新笔记需要冷启动的原因
- 新笔记缺少与用户的交互,导致推荐的难度大、效果差
- 扶持新发布、低曝光的笔记,可以增强作者发布意愿
优化冷启的目标
- 精准推荐:克服冷启的困难,把新笔记推荐给合适的用户,不引起用户反感
- 激励发布:流量向低曝光新笔记倾斜,激励作者发布
- 挖掘高潜:通过初期小流量的试探,找到高质量的笔记,给与流量倾斜
评价指标
- 作者侧指标:反映用户的发布意愿
- 发布渗透率、人均发布量。
- 低曝光扶持越好,作者侧指标越好。
- 用户侧指标:反映推荐是否精准,是否会引起用户反感
- 新笔记指标:新笔记的点击率、交互率。推荐的准,这个指标会好看。
- 大盘指标:消费时长、日活、月活。
- 冷启动不是促进消费指标增长,但是也不能显著伤害消费指标,应该尽量让消费指标持平。
- 内容侧指标:反映冷启是否能挖掘优秀笔记
- 类似于30天内点击超过1000的笔记
- 高热笔记占比,小红书应该也用了。
- 作者侧指标:反映用户的发布意愿
作者侧指标
- 发布渗透率(penetration rate)
- 发布渗透率 = 当日发布人数 / 日活人数,发布一篇或以上,就算一个发布人数,例:
- 当日发布人数 = 100 万
- 日活人数 = 2000 万
- 发布渗透率 = 100 / 2000 = 5%
- 发布渗透率 = 当日发布人数 / 日活人数,发布一篇或以上,就算一个发布人数,例:
- 人均发布量
- 人均发布量 = 当日发布笔记数 / 日活人数,例:
- 每日发布笔记数 = 200 万
- 日活人数 = 2000 万
- 人均发布量 = 200 / 2000 = 0.1
- 人均发布量 = 当日发布笔记数 / 日活人数,例:
- 发布渗透率、人均发布量反映出作者的发布积极性
- 冷启的重要优化目标是促进发布,增大内容池
- 新笔记获得的曝光越多,首次曝光和交互出现得越早,作者发布积极性越高
- 发布渗透率(penetration rate)
用户侧指标
- 新笔记的消费指标
- 新笔记的点击率、交互率
- 问题:曝光的基尼系数很大
- 即少量头部新笔记推送准确,但大部分新笔记的推送不准,综合下来点击率、交互率也很高
- 少数头部新笔记占据了大部分的曝光
- 新笔记的点击率、交互率
- 分别考察高曝光、低曝光新笔记
- 高曝光:比如 >1000 次曝光
- 低曝光:比如 <1000 次曝光
- 大盘消费指标(不区分新老笔记)
- 优化冷启时,不是为了提升大盘指标,而是确保新策略不显著伤害大盘指标
- 大盘的消费时长、日活、月活
- 新笔记扶持有跷跷板效应,大力扶持低曝光新笔记会发生什么?
- 作者侧发布指标变好
- 用户侧大盘消费指标变差(损害用户体验)
- 新笔记的消费指标
内容侧指标
- 高热笔记占比
- 高热笔记:前 30 天获得 1000+ 次点击
- 高热笔记占比越高,说明冷启阶段挖掘优质笔记的能力越强
冷启动优化点
- 优化全链路(召回、排序等)
- 流量调控(流量如何在新老笔记中分配)
Item Cold Start: Simple Recall Channel
召回的依据
- ✔ 自带图片、文字、地点
- ✔ 算法或人工标注的标签
- ❌ 没有用户点击、点赞等信息。这些信息可以反映笔记的质量,以及哪类用户喜欢该笔记
- ❌ 没有笔记 ID embedding。ID embedding 是从用户和笔记的交互中学习出来的
双塔模型是推荐系统中最重要的召回通道,没有之一。离开双塔模型,很难做好新笔记的推荐。同时影响召回和排序。
冷启动召回的困难
- 缺少用户交互,还没学好笔记 ID embedding,导致双塔模型效果不好。
- 缺少用户交互,导致 ItemCF 不适用。
召回通道
- ❌ ItemCF 召回(不适用)
- ❔ 双塔模型(改造后适用)
- ✔ 类目、关键词召回(适用)
- ✔ 聚类召回(适用)
- ✔ Look-Alike 召回(适用)
ID Embedding Improvement
ID Embedding的改进
- 改进方案 1:新笔记使用 default embedding
- 物品塔做 ID embedding 时,让所有新笔记共享一个 ID,而不是用自己真正的 ID
- Default embedding:共享的 ID 对应的 embedding 向量,学出来的 Default embedding 比随机初始化一个 ID embedding 要好。
- 到下次模型训练的时候,新笔记才有自己的 ID embedding 向量
- 改进方案 2:利用相似笔记 embedding 向量
- 查找 top k 内容最相似的高曝笔记
- 把 k 个高曝笔记的 embedding 向量取平均,作为新笔记的 embedding
- 之所以用高曝笔记,是因为它们的 embedding 通常学得比较好
- 改进方案 1:新笔记使用 default embedding
多个向量召回池
- 多个召回池,让新笔记有更多曝光机会
- 1 小时新笔记
- 6 小时新笔记
- 24 小时新笔记
- 30 天笔记
- 所有召回池共享同一个双塔模型,那么多个召回池不增加训练的代价。
- 多个召回池,让新笔记有更多曝光机会
Category and keyword recall
类目召回
用户画像
- 感兴趣的类目:美食、科技数码、电影……
- 感兴趣的关键词:纽约、职场、搞笑、程序员、大学……
基于类目的召回
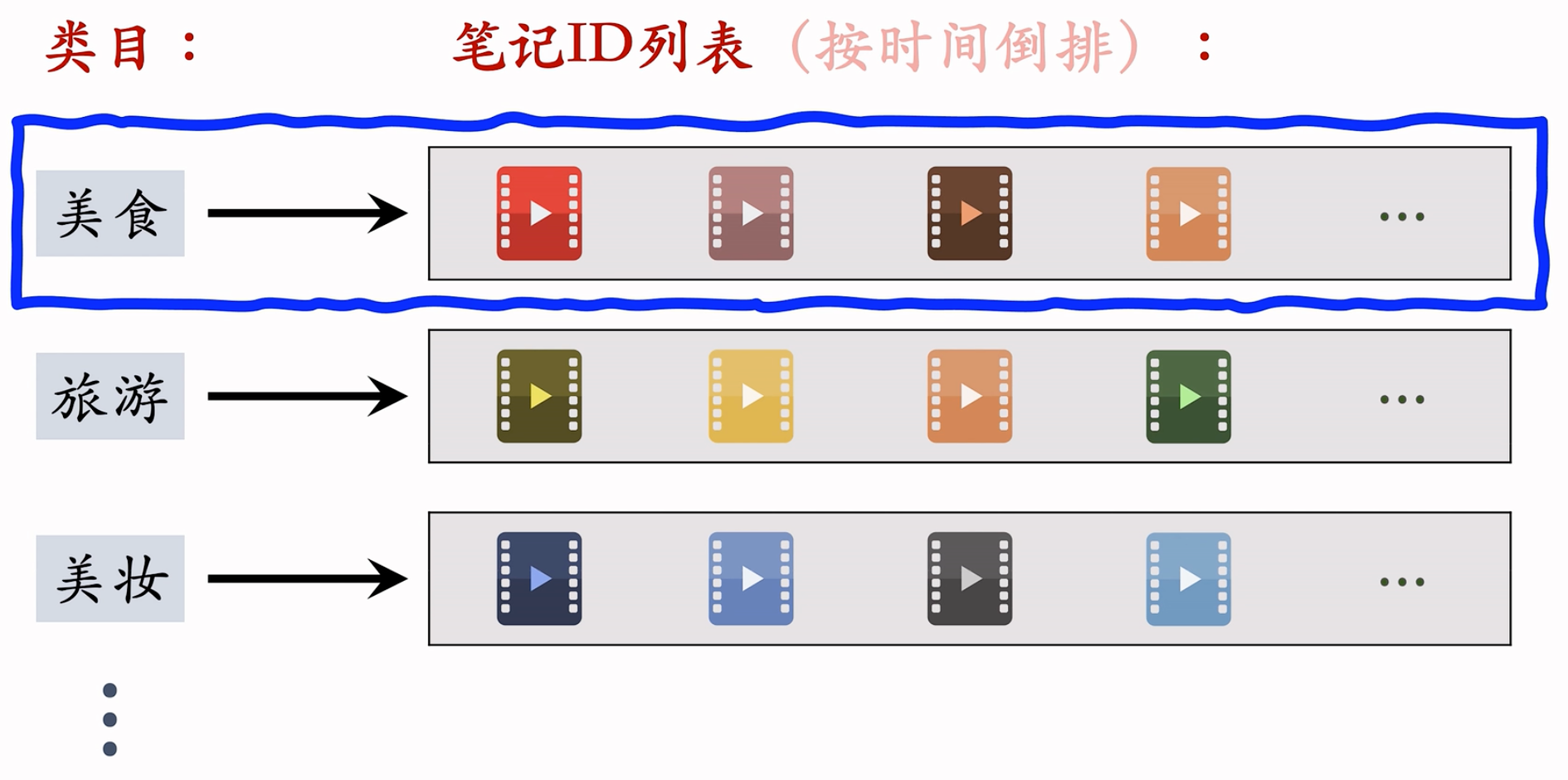
- 系统维护类目索引:类目 → 笔记列表(按时间倒排)
- 用类目索引做召回:用户画像 → 类目 → 笔记列表
- 取回笔记列表上前 k 篇笔记(即最新的 k 篇)
基于关键词的召回
- 系统维护关键词索引:关键词 → 笔记列表(按时间倒排)
- 根据用户画像上的关键词做召回
- 和上面的没啥区别,只是把关键词 -> 类目。
缺点:
- 缺点 1:只对刚刚发布的新笔记有效
- 取回某类目/关键词下最新的 k 篇笔记。
- 发布几小时之后,就再没有机会被召回。“留给每篇笔记的窗口期很短”
- 所以应该在用户高频使用软件的时间段发布内容
- 缺点 2:弱个性化,不够精准
- 类目/关键词还是太大了
- 比如我喜欢观赏鱼,但是我搜索的是宠物。推荐给我的新笔记大多数都是猫猫狗狗,我就不感兴趣。
Cluster recall
聚类召回是基于物品内容的召回通道。它假设如果用户喜欢一个物品,那么用户会喜欢内容相似的其他物品。使用聚类召回,需要事先训练一个多模态神经网络,将笔记图文表征为向量,并对向量做聚类,然后建索引。冷启动的时候特别有用!
聚类召回
- 基本思想
- 如果用户喜欢一篇笔记,那么他会喜欢内容相似的笔记
- 事先训练一个神经网络,基于笔记的类目和图文内容,把笔记映射到向量
- 对笔记向量做聚类,划分为 1000 cluster,记录每个 cluster 的中心方向(k-means 聚类,用余弦相似度)
- 聚类索引
- 一篇新笔记发布之后,用神经网络把它的图文内容映射到一个特征向量
- 从 1000 个向量(对应 1000 个 cluster)中找到最相似的向量,作为新笔记的 cluster
- 索引:cluster → 笔记 ID 列表(按时间倒排)
- 线上召回
- 给定用户 ID,找到他的 last-n 交互的笔记列表,把这些笔记作为种子笔记
- 把每篇种子笔记映射到向量,寻找最相似的 cluster(知道了用户对哪些 cluster 感兴趣)
- 从每个 cluster 的笔记列表中,取回最新的 $m$ 篇笔记
- 最多取回 $mn$ 篇新笔记
- 感觉就是基于内容的推荐呀!聚类召回与类目召回的缺点相同:只对刚发布的新笔记有效
- 基本思想
内容相似度模型
提取图文表征
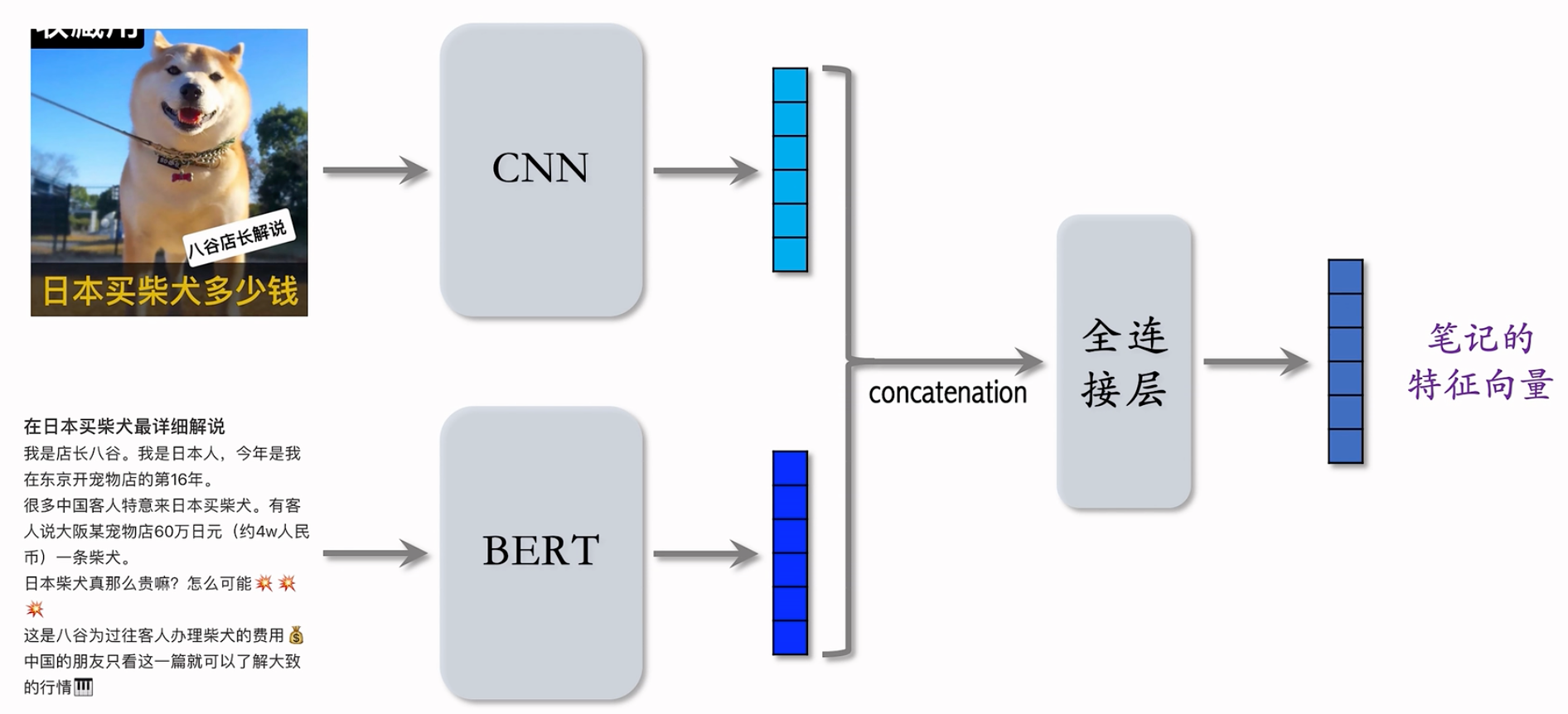
聚类召回通过内容相似度模型来把笔记映射到向量。
左右两个用的神经网络的参数是相同的
CNN 和 BERT 可以用预训练模型,全连接层是随机初始化后训练出来的
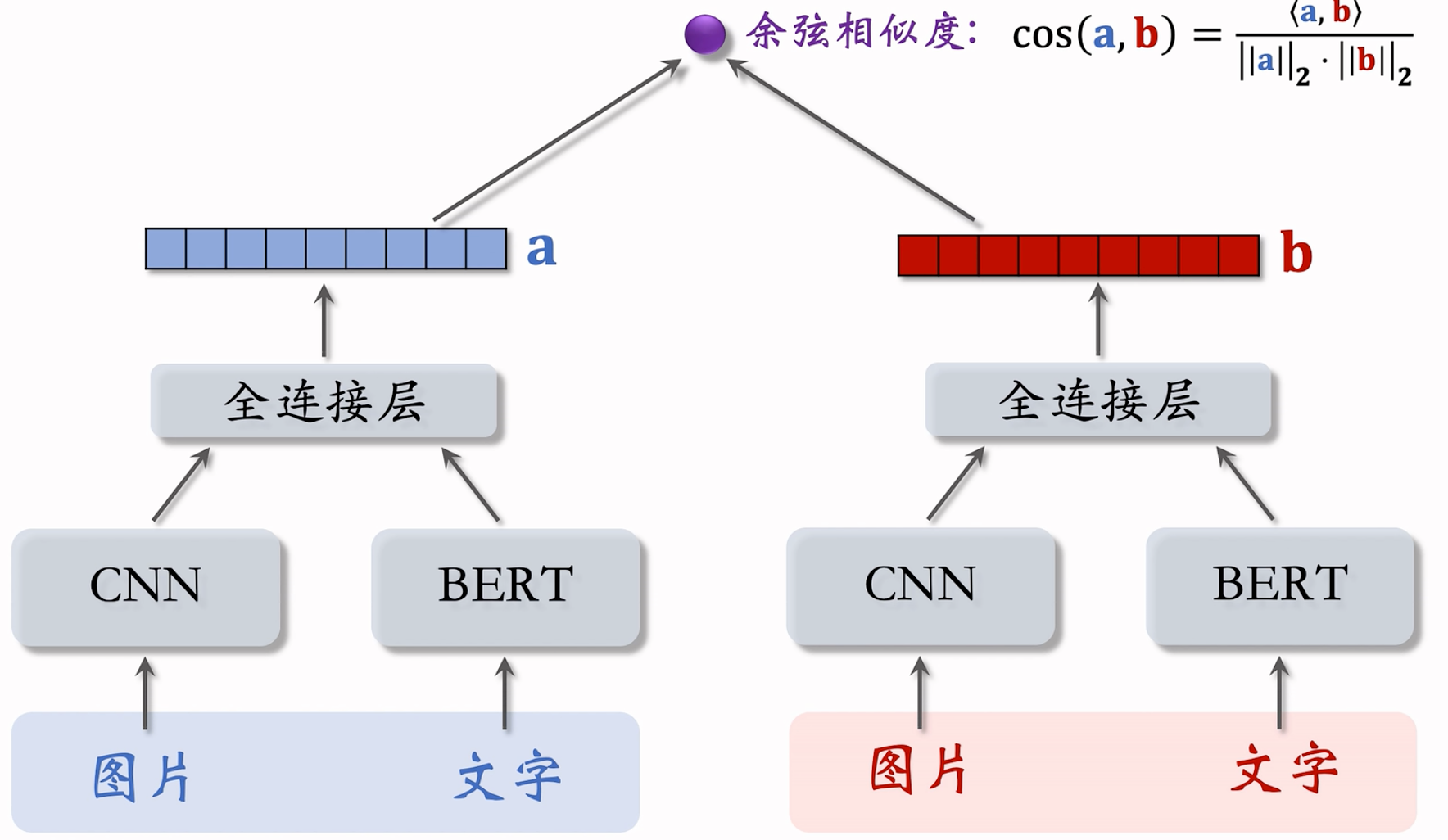
训练内容相似度模型
模型结构:
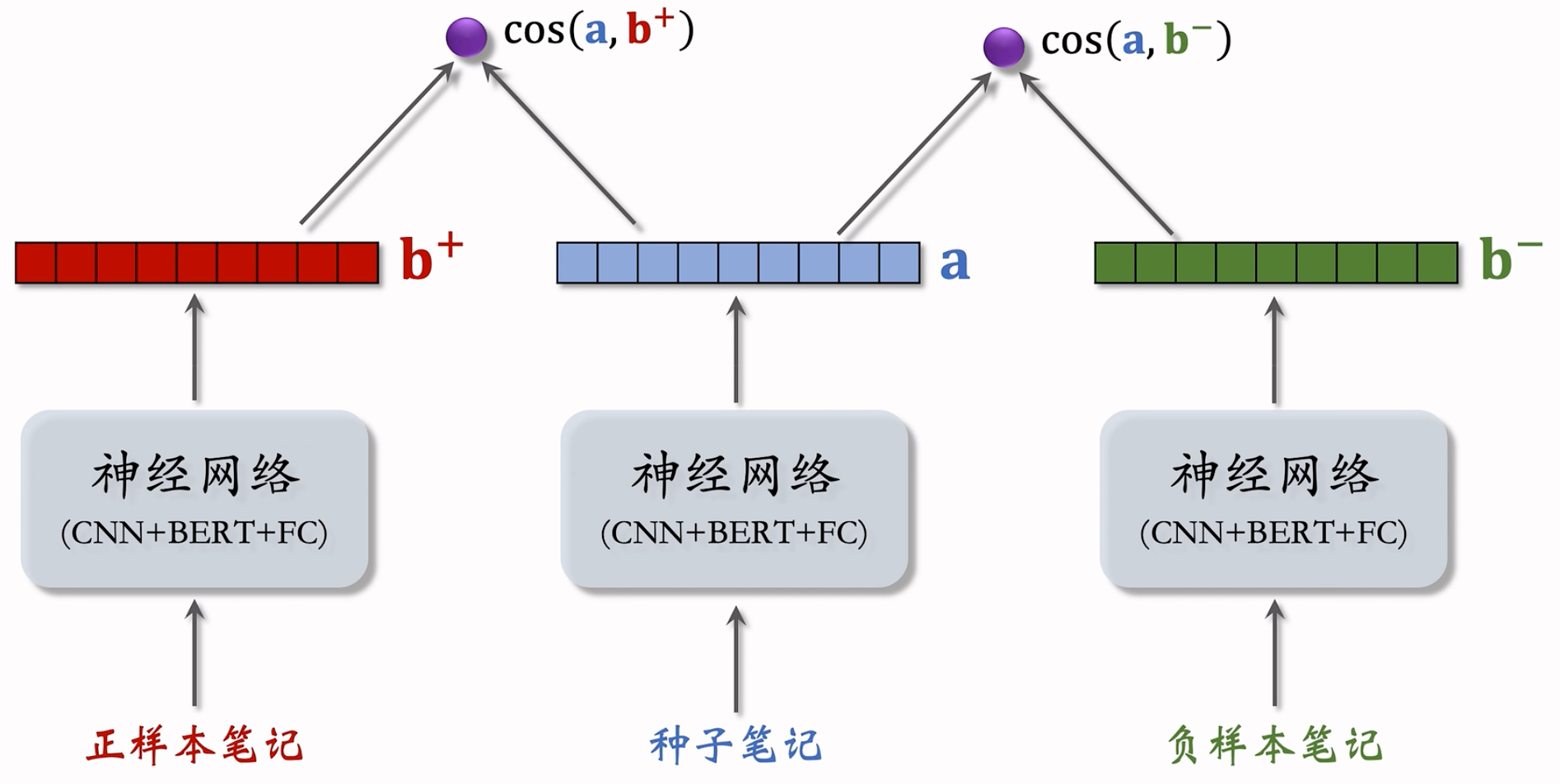
给定用户 ID,找到他的 last-n 交互的笔记列表,把这些笔记作为种子笔记
基本想法:鼓励 $\cos{(\bold{a},\bold{b}^+)}$ 大于 $\cos{(\bold{a},\bold{b}^-)}$
- Triplet hinge loss: $L(\bold{a},\bold{b}^+,\bold{b}^-)=\max{\{ 0,\cos{(\bold{a},\bold{b}^-)}+m-\cos{(\bold{a},\bold{b}^+)}\}}$ {#
- Triplet logistic loss: $L(\bold{a},\bold{b}^+,\bold{b}^-)=\log{( 1+\exp{·(\cos{(\bold{a},\bold{b}^-)}-\cos{(\bold{a},\bold{b}^+))})}}$ {#
此处的公式与召回 - 双塔模型 - Pairwise 训练中相似
< 种子笔记,正样本 >
- 方法一:人工标注二元组的相似度,人工标注代价大,不划算。
- 方法二:算法自动选正样本
- 筛选条件:
- 只用高曝光笔记作为二元组(因为有充足的用户交互信息)
- 两篇笔记有相同的二级类目,比如都是“菜谱教程”(过滤掉不相似的样本,缩小查找范围)
- 用 ItemCF 的物品相似度选正样本
- 筛选条件:
< 种子笔记,负样本 >
- 从全体笔记中随机选出满足条件的笔记:
- 字数较多(神经网络提取的文本信息有效)
- 笔记质量高,避免图文无关
- 从全体笔记中随机选出满足条件的笔记:
聚类召回总结
- 基本思想:根据用户的点赞、收藏、转发记录,推荐内容相似的笔记
- 线下训练:多模态神经网络把图文内容映射到向量
- 线上服务:用户历史喜欢的笔记 → 特征向量 → 最近的 Cluster → 每个 Cluster 上的新笔记
Look-Alike recall
Look-Alike 是一种召回通道,对冷启很有效。Look-Alike 适用于发布一段时间、但是点击次数不高的物品。物品从发布到热门,主要的透出渠道会经历三个阶段:
- 类目召回、聚类召回。它们是基于内容的召回通道,适用于刚刚发布的物品。
- Look-Alike 召回。它适用于有点击,但是点击次数不高的物品。
- 双塔、ItemCF、Swing 等等。它们是基于用户行为的召回通道,适用于点击次数较高的物品。
Look-Alike起源于互联网广告
用明确的目标用户画像。
但是实际上很多用户没有那么详细的信息。
从已知种子用户 -> 含有很多未知信息的用户。
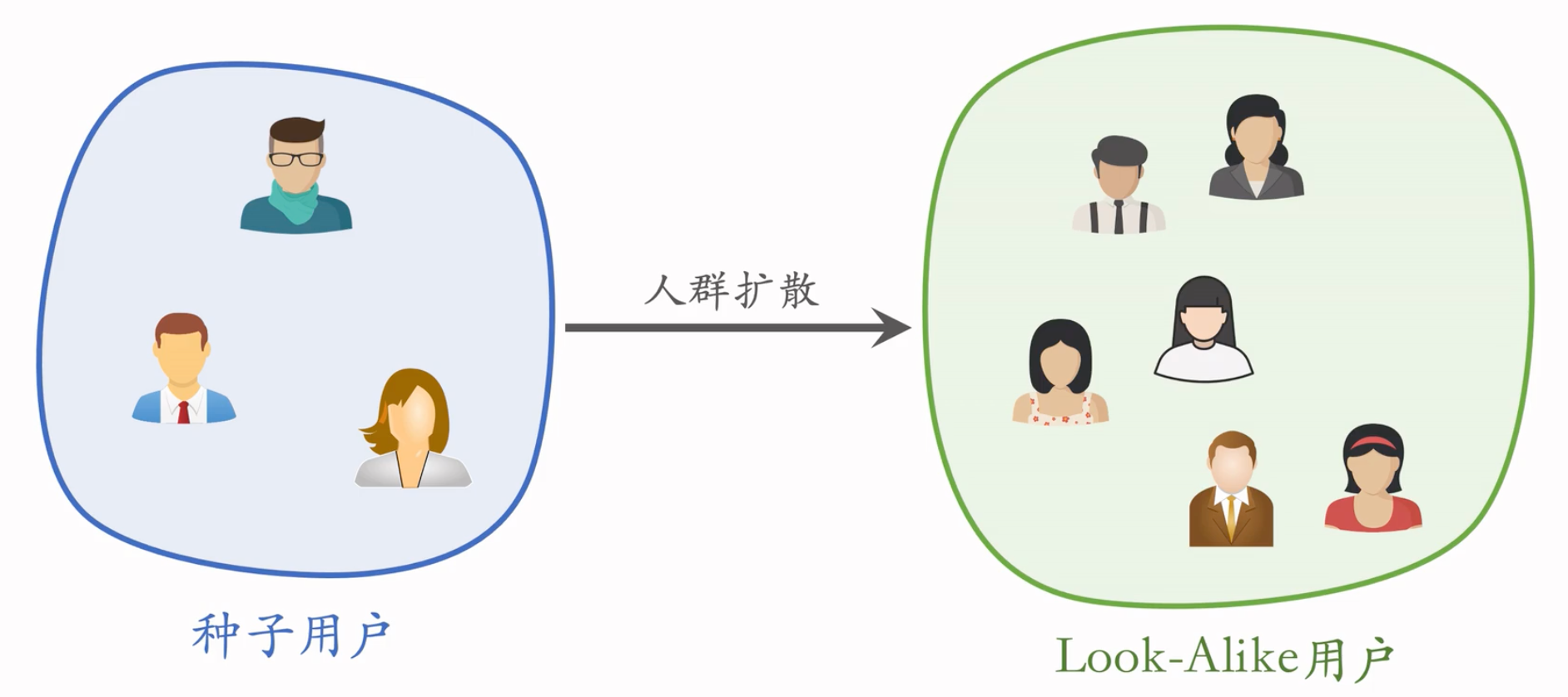
如何计算两个用户的相似度?
- UserCF:两个用户有共同的兴趣点
- Embedding:两个用户向量的 cosine 较大
Look-Alike 用于新笔记召回
点击、点赞、收藏、转发—用户对笔记可能感兴趣
系统把新笔记推荐给了许多用户,由于是新笔记,所以受众不太精准。而跟新笔记进行了交互用户,就成了种子用户。
用双塔模型学习种子用户的向量,然后取均值,把得到的向量作为 新笔记 的表征
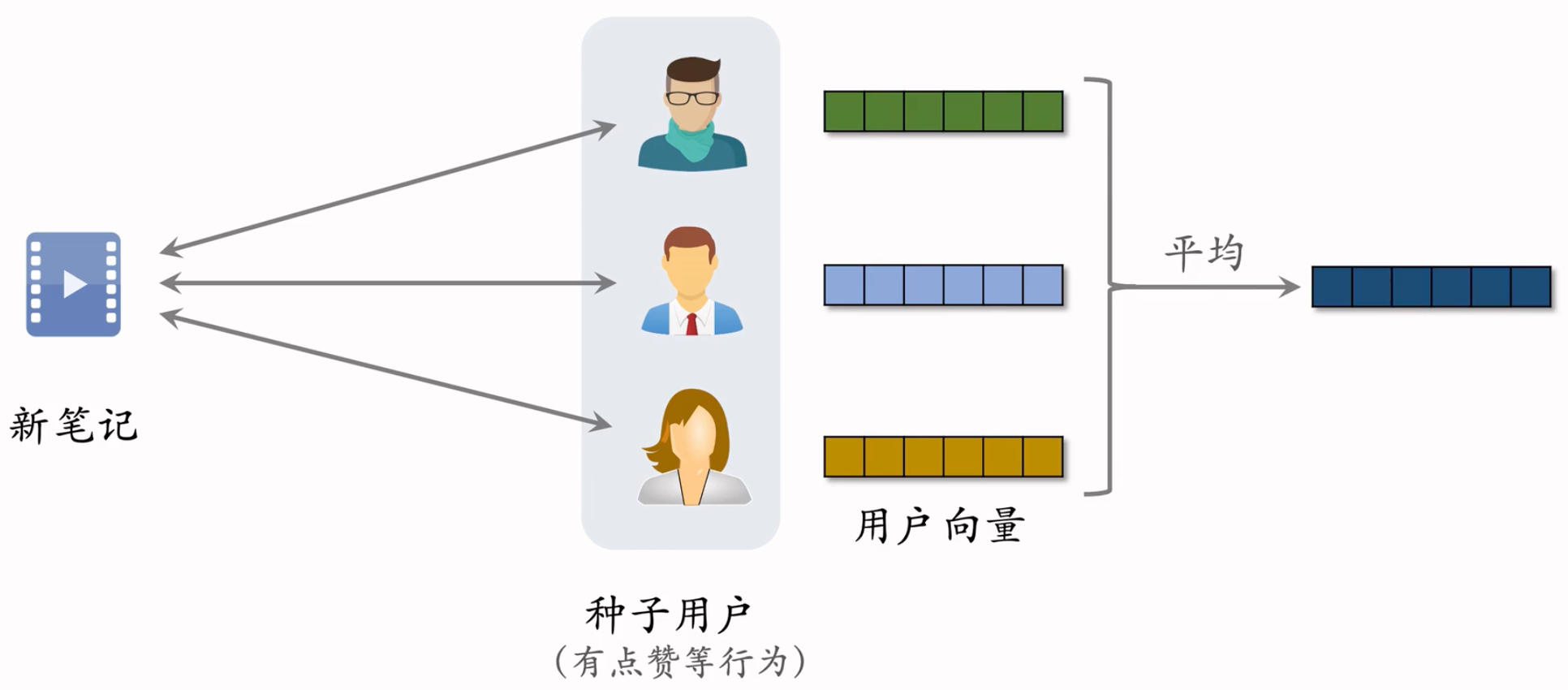
把得到的新的向量作为用户的表征。代表什么样的用户对于笔记感兴趣。
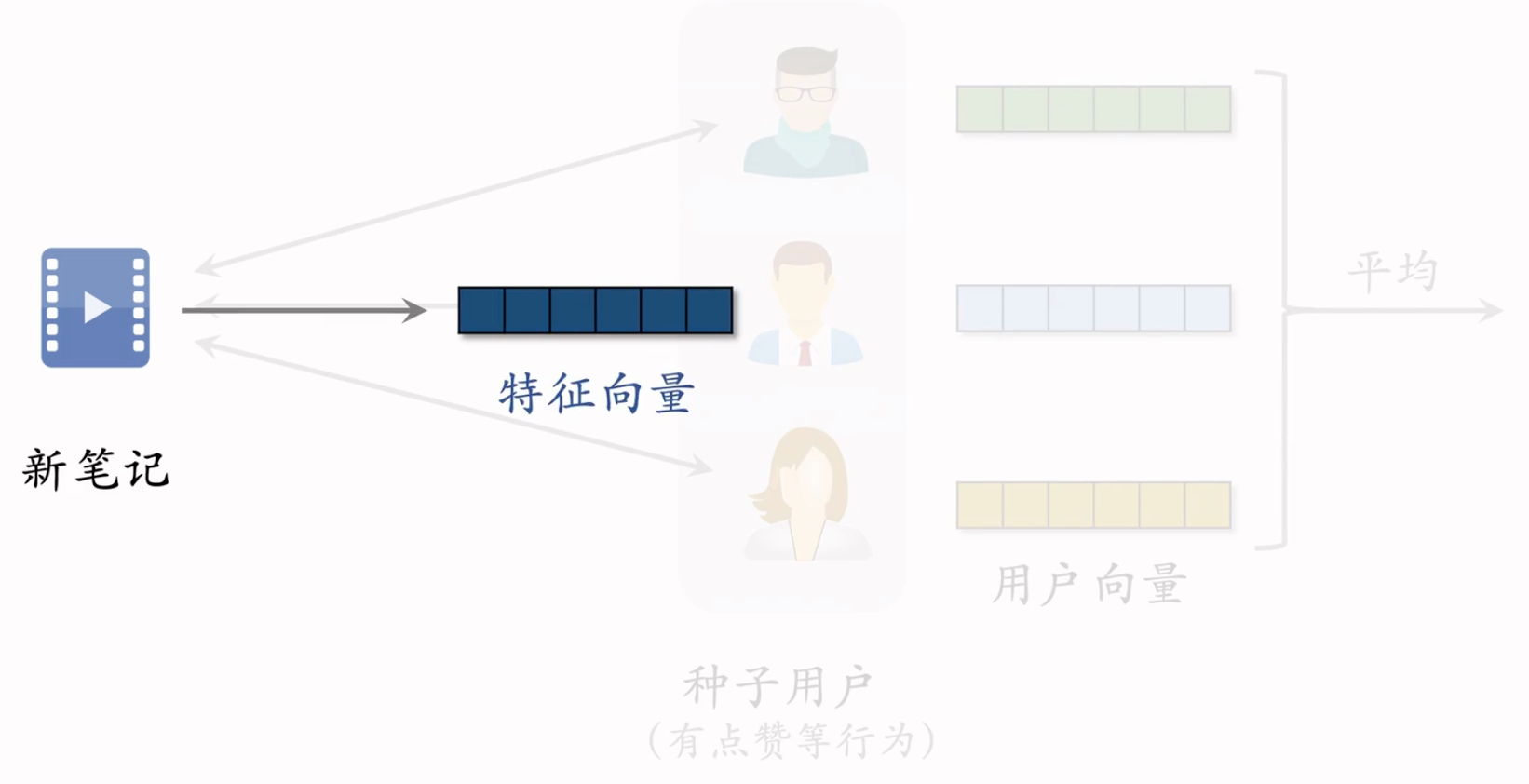
近线更新特征向量,近线:不用实时更新,做到分钟级更新即可
此处是做到每当有新交互发生后,几分钟内更新特征向量。特征向量是有交互的用户的向量的平均。
每当有用户交互该物品,更新笔记的特征向量
交互流程
根据上面的流程,得到很多笔记的Embedding,存在向量数据库里面。
给用户做推荐的时候,用双塔计算用户的Embedding,去向量数据库里面做最近邻查找,取回几十篇笔记。
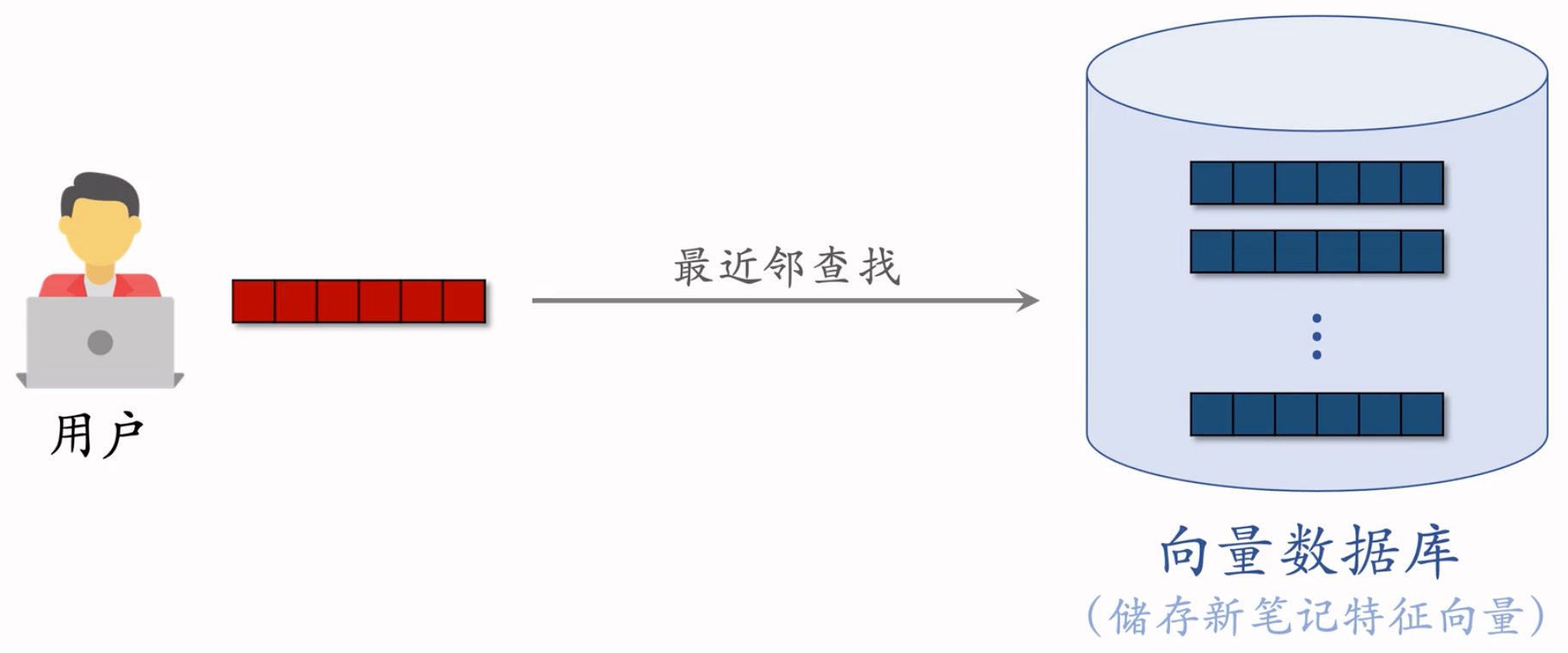
这个召回通道就叫 Look-Alike
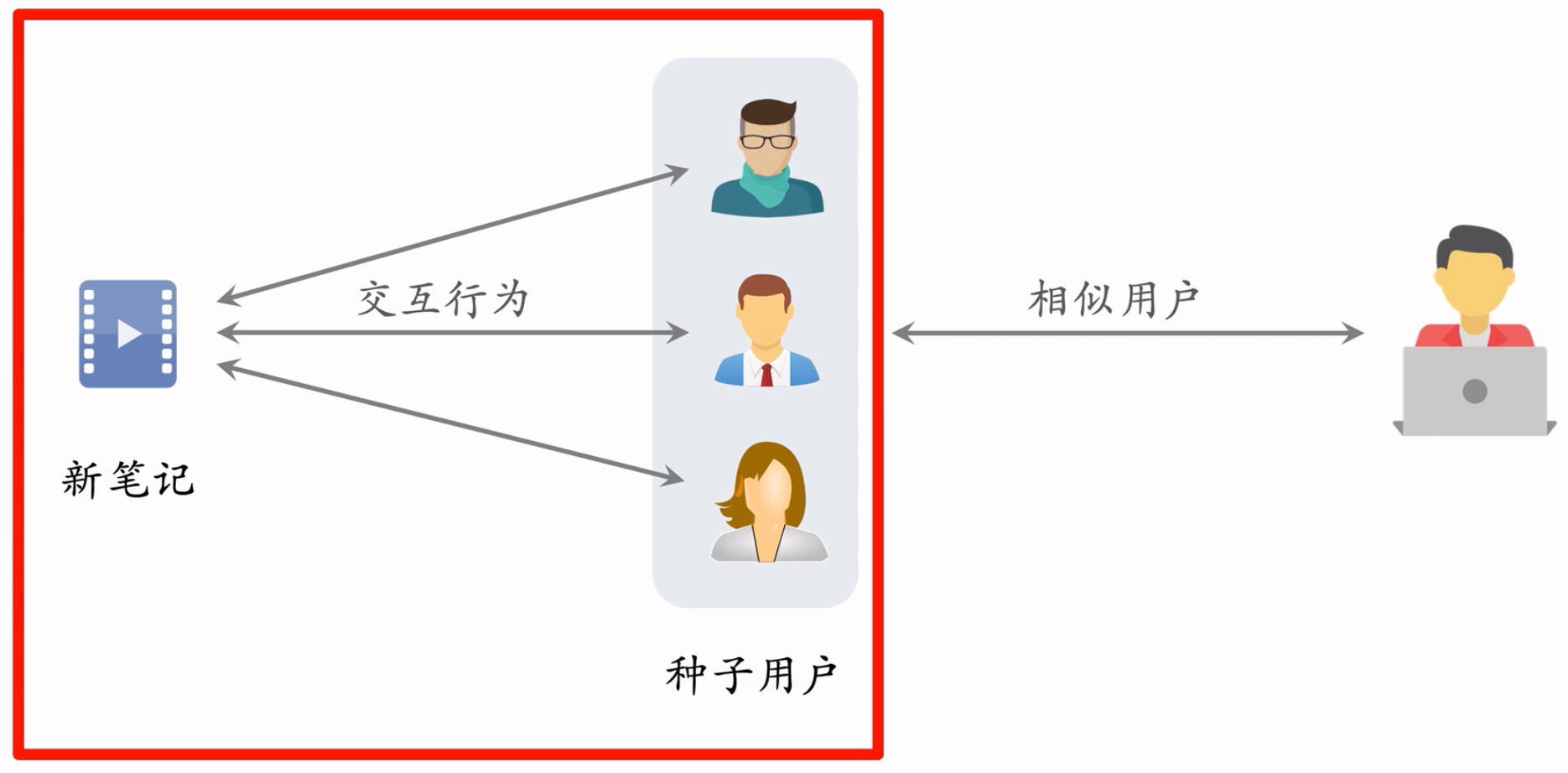
小红书的look-alike,和广告领域的look-alike原理是相同的:
Traffic Control
- 冷启动的优化点
- 优化全链路(包括召回和排序)
- 流量调控(流量怎么在新物品、老物品中分配)
- 工业界的通常做法是扶持新笔记
- 扶持新笔记的目的
- 目的 1:促进发布,增大内容池
- 新笔记获得的曝光越多,作者创作积极性越高
- 反映在发布渗透率、人均发布量
- 目的 2:挖掘优质笔记
- 做探索,让每篇新笔记都能获得足够曝光
- 挖掘的能力反映在高热笔记占比
- 目的 1:促进发布,增大内容池
- 工业界的做法
- 假设推荐系统只分发年龄 <30 天的笔记。
- 假设采用自然分发,新笔记(年龄 <24 小时)的曝光占比为 1/30,扶持新笔记,让新笔记的曝光占比远大于 1/30。
- 流量调控技术的发展
- 在推荐结果中强插新笔记(落后技术)
- 对新笔记的排序分数做提权(boost)
- 较为复杂,难点在于调整权重
- 投入产出比很划算的策略,效果还可以。实现不难,抖音、小红书前期都这么做。
- 通过提权,对新笔记做保量。高级技术!复杂精细化的提权,例如:1h内曝光必须最少是100。
- 差异化保量:根据内容质量,确定保量目标。质量越高,流量倾斜越多,保量目标越高。
New Notes Boost
- 系统的链路
- 目标:让新笔记有更多机会曝光
- 如果做自然分发,24 小时新笔记占比为 1/30
- 做人为干涉,让新笔记占比大幅提升
- 干涉粗排、重排环节,给新笔记提权
- 优点:容易实现,投入产出比好
- 缺点:
- 曝光量对提权系数很敏感
- 很难精确控制曝光量,容易过度曝光和不充分曝光
- 目标:让新笔记有更多机会曝光
New Notes Guarantee
保量:不论笔记质量高低,都保证 24 小时获得 100 次曝光
在原有提权系数的基础上,乘以额外的提权的系数,比如:
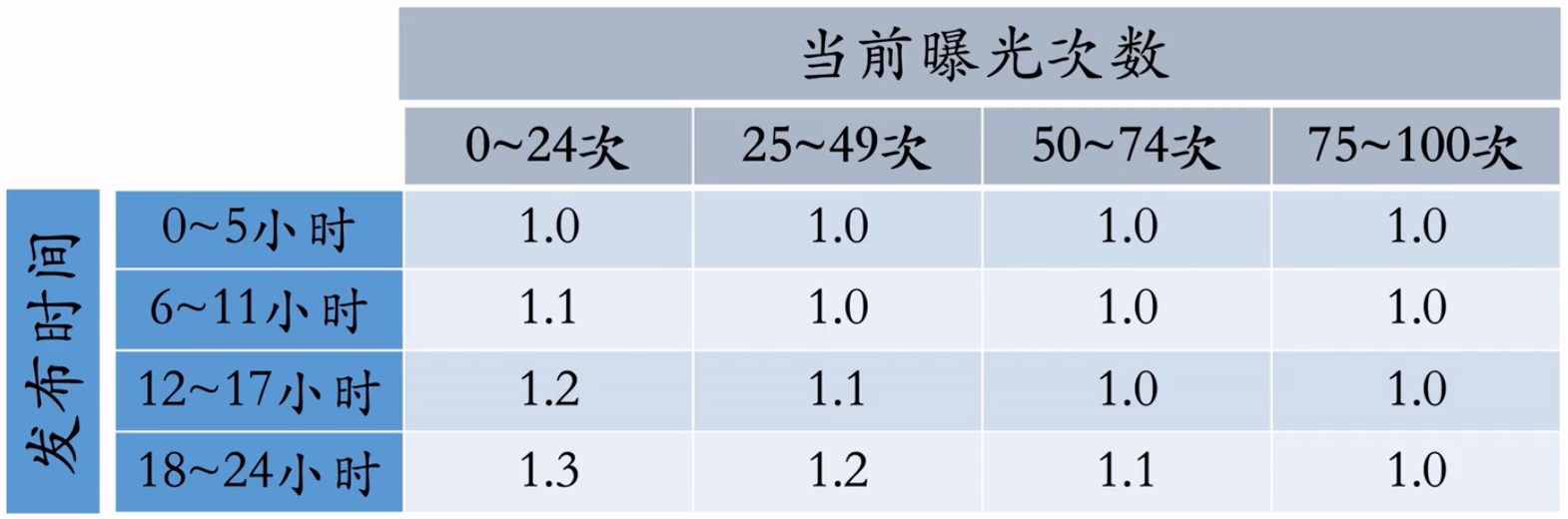
动态提权保量:用下面四个值计算提权系数
- 目标时间:比如 24 小时
- 目标曝光:比如 100 次
- 发布时间:比如笔记已经发布 12 小时
- 已有曝光:比如笔记已经获得 20 次曝光
提权系数 =$f(\frac{发布时间}{目标时间},\frac{已有曝光}{目标曝光})=f(0.5,0.2)$
保量的难点
- 保量成功率远低于 100%
- 很多笔记在 24 小时达不到 100 次曝光
- 召回、排序存在不足
- 提权系数调得不好
- 线上环境变化会导致保量失败
- 线上环境变化:新增召回通道、升级排序模型、改变重排打散规则……
- 线上环境变化后,需要调整提权系数
- 保量成功率远低于 100%
思考题
- 是否可以给所有新笔记一个很大的提权系数(比如 4 倍),直到达成 100 次曝光为止,然后再把权重恢复呢?
- 这样的保量成功率很高
- 为什么不用这种方法呢?
- 给新笔记分数 boost 越多,对新笔记越有利?
- 好处:分数提升越多,曝光次数越多
- 坏处:把笔记推荐给不太合适的受众
- 点击率、点赞率等指标会偏低
- 笔记长期会受推荐系统打压,难以成长为热门笔记:即这个笔记如果推荐给合适用户,那它是不错的,但强行提高曝光次数,导致它被经常推给不适合的用户,进而交互指标偏低。
- 是否可以给所有新笔记一个很大的提权系数(比如 4 倍),直到达成 100 次曝光为止,然后再把权重恢复呢?
Differentiated quality assurance
- 保量:不论新笔记质量高低,都做扶持,在前 24 小时给 100 次曝光
- 差异化保量:不同笔记有不同保量目标,普通笔记保 100 次曝光,内容优质的笔记保 100~500 次曝光
- 基础保量:24 小时 100 次曝光
- 内容质量:用模型评价内容质量高低,给予额外保量目标,上限是加 200 次曝光
- 作者质量:根据作者历史上的笔记质量,给予额外保量目标,上限是加 200 次曝光
- 一篇笔记最少有 100 次保量,最多有 500 次保量。达到保量目标后,就会停止扶持,新笔记和老笔记公平竞争。
A/B Test
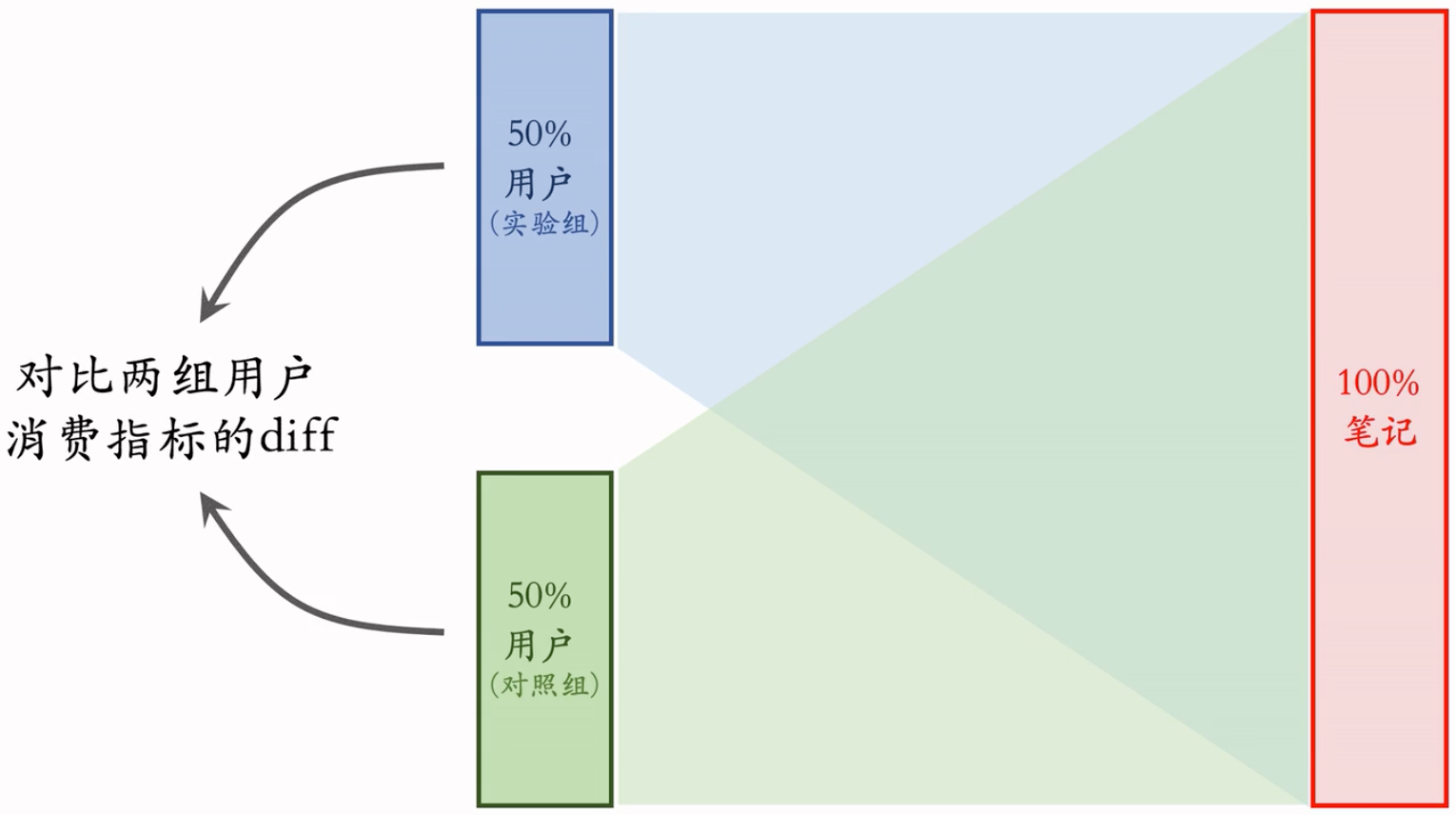
这节课的内容是物品冷启动的AB测试,内容很烧脑,不建议初学者观看。推荐系统常用的A/B测试只考察用户侧消费指标,而推荐系统的AB测试还需要额外考察作者侧发布指标。后者远比前者复杂,而且所有已知的实验方案都存在缺陷。
冷启动AB测试
- 作者侧(发布)指标:发布渗透率、人均发布量。
- 用户侧(消费)指标:
- 对新笔记的点击率、交互率
- 大盘指标:消费时长、日活、月活。(标准AB测试)
- 标准的 AB 测试只测大盘指标,而冷启动 AB 测试还要测上面提到的指标
标准的A/B测试:
冷启动的A/B测试:主要测用户侧的消费指标,还有作者侧的发布指标
用户侧实验:
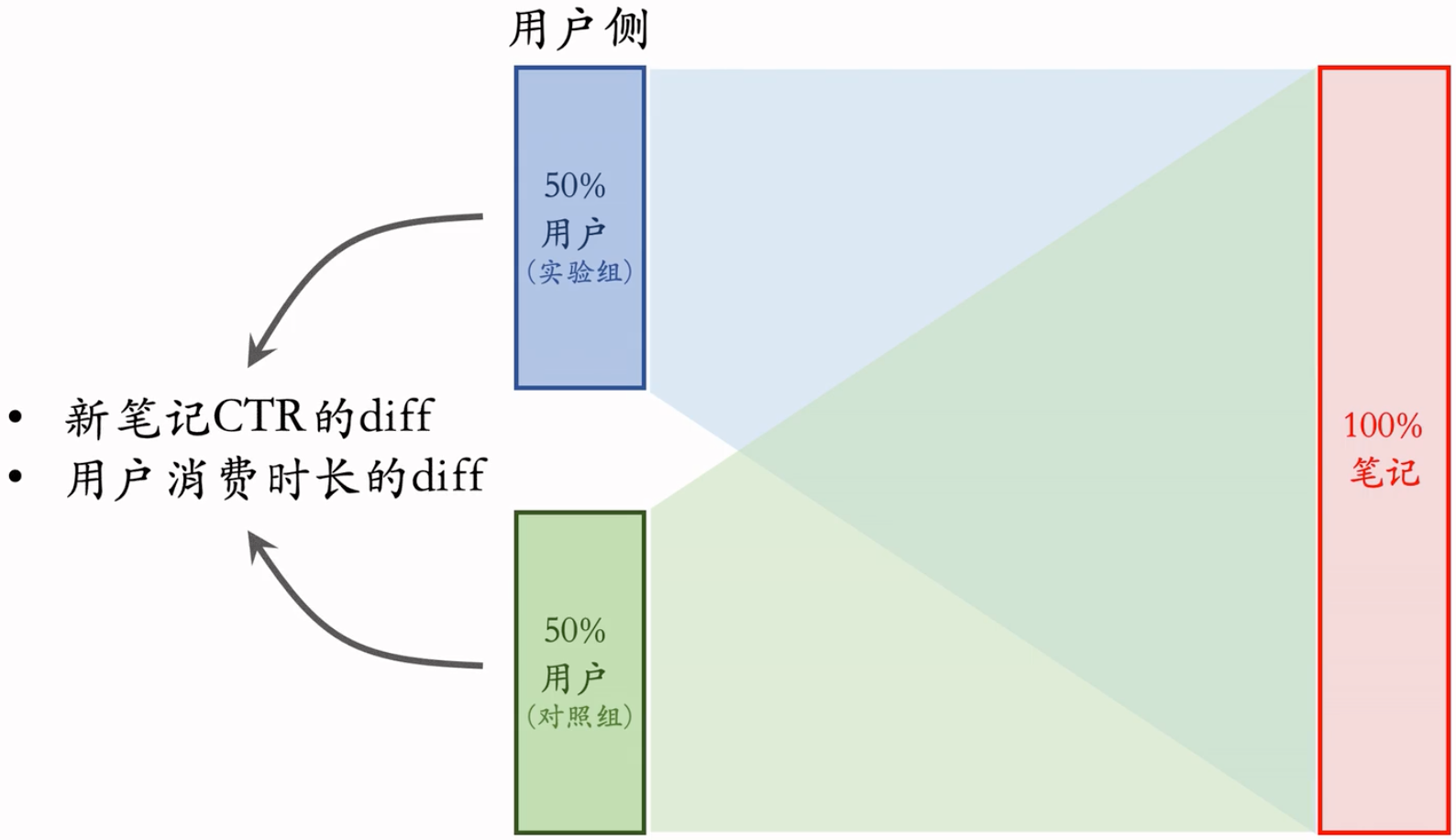
限定:保量 100 次曝光
假设:新笔记曝光越多,用户使用 APP 时长越低:这个假设很合理,因为新笔记推送不准确,过多会影响体验
新策略:把新笔记排序时的权重增大两倍
结果(只看消费指标):
- AB 测试的 diff 是负数(策略组不如对照组)。
- 如果推全,diff 会缩小(比如 −2% → −1%)。新策略对用户体验的伤害,没有A/B test观测到的那么严重。Why?
为什么会有上面的diff深入探讨:
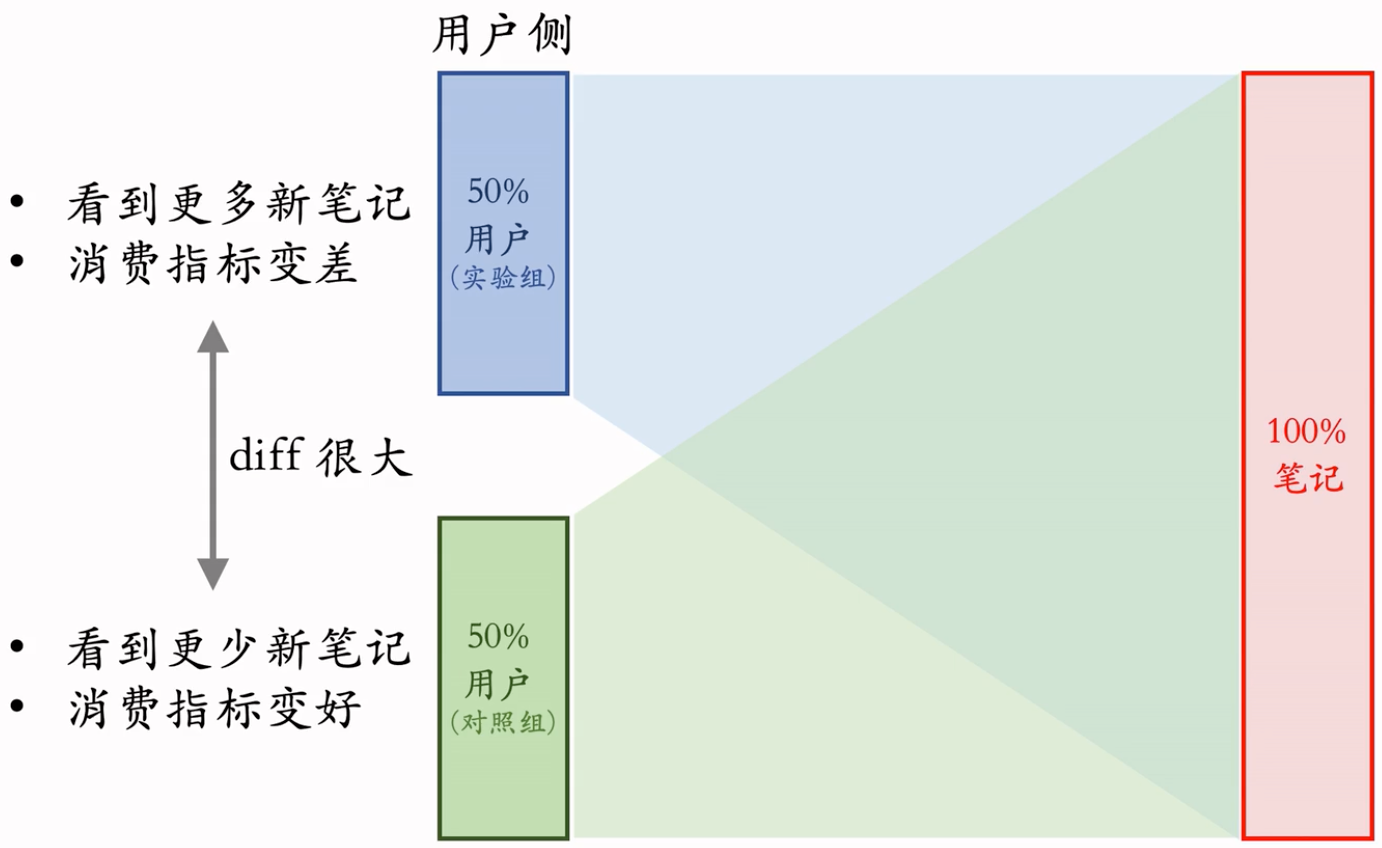
- 使用新策略后,实验组看到的新笔记会增多,又因为有着保量 100 次的目标,所以对照组看到的新笔记数量会减少。
- 实验组看多了新笔记,消费指标变差;对照组看少了新笔记,消费指标变好。
- 但推全后,这 100 次的保量目标会均匀的分配给所有用户,消费指标依然会下降,但不会有实验组那么差。 -> GPT如是说到:在实验组中,用户被强制看到至少100次新笔记,这可能导致用户感到疲劳或者不满,因为他们可能觉得内容过多或者不感兴趣。这种强制性的展示可能会对用户体验产生负面影响,从而导致消费指标的显著下降。(100次曝光都在这一小部分人群之中)然而,在推全后,虽然所有用户都会看到更多的新笔记,但这种展示不会像实验组那样强制性和频繁。这意味着用户可能会有更多的选择和控制权,从而减少对用户体验的负面影响。因此,虽然消费指标可能会有所下降,但下降的幅度不会像实验组那样剧烈。
作者侧实验
- 作者侧实验不好做,没有很完美的实验方案。
Option 1
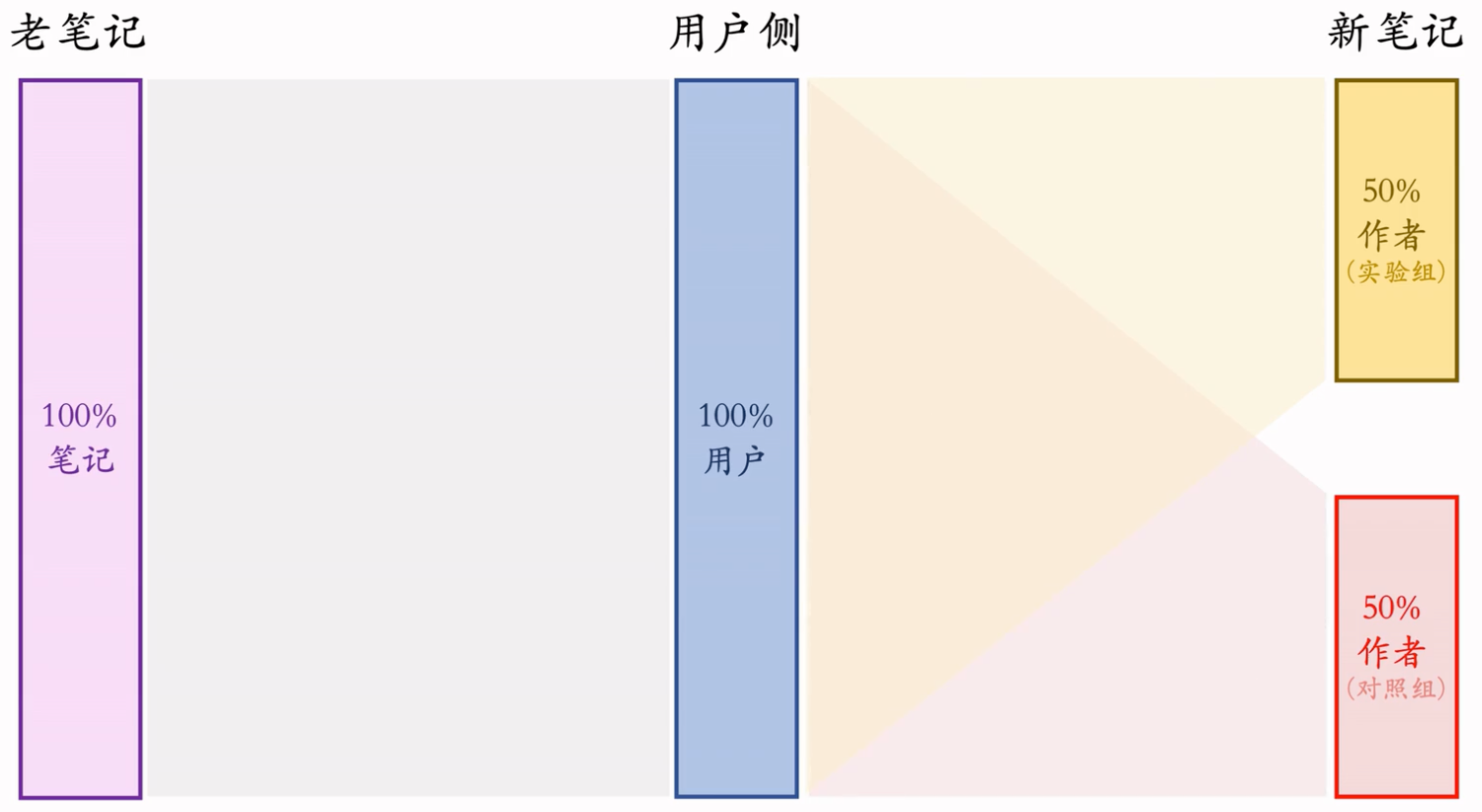
严重缺点:新笔记会抢夺流量。存在现象:实验观测到diff,但是推全后,发布指标没有发生任何变化。
缺点汇总:
缺点一:新笔记之间会抢流量

- 设定:
- 新老笔记走各自队列,没有竞争(完全独立)
- 重排分给新笔记 1/3 流量,分给老笔记 2/3 流量,两者曝光比例固定
- 新策略:把新笔记重拍的权重增大两倍
- 新笔记和老笔记公平竞争。这对新笔记来说依然是公平竞争,因为新笔记有自己的队列,只和新笔记竞争呀。而新笔记在重排中还是 1/3 流量。
- 所以新策略不会激励发布,不会改变发布侧指标。
- 结果(只看发布指标):
- AB 测试的 diff 是正数(实验组优于对照组)。为啥?因为提权后的实验组新笔记,会抢走对照组的曝光,因为实验组和对照组是公平竞争的。实验组提权后,曝光变多了,实验组指标肯定也就涨了,对照组也就跌了,这就有diff了。
- 如果推全,diff 会消失(比如 2% → 0)。在我们的设定下,新笔记权重 x 2不改变发布指标,只改变曝光量。推全后,发布侧指标就和之前一样了。
- 道理:A/B观测到的Diff是不可信的,推全之后可能会消失。
- 给实验组新笔记提权后,同是新笔记,实验组中的能获得更多曝光,而对照组中的曝光就少了。
- 而一旦推全后,就不存在新笔记间强流量的情况,diff 就消失了。
- 设定:
缺点二:新笔记和老笔记抢流量
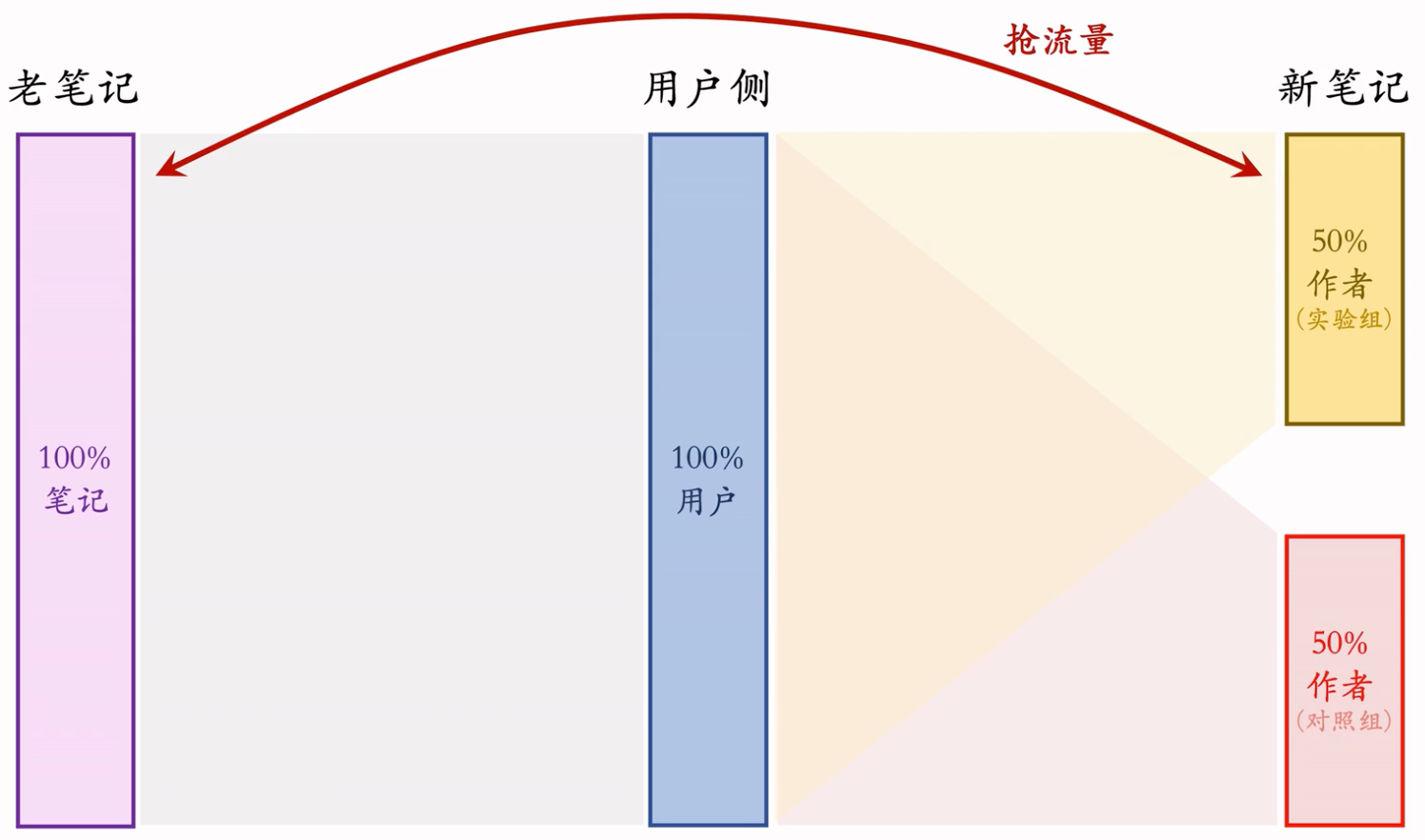
- 举例说明
- 设定:新老笔记自由竞争
- 新策略:把新笔记排序时的权重增大两倍
- AB 测试时,50% 新笔记(带策略)跟 100% 老笔记抢流量。一份新笔记,抢两份老笔记的流量。
- 推全后,100% 新笔记(带策略)跟 100% 老笔记抢流量。一份新笔记只抢一份老笔记的流量,更难抢到流量!
- 作者侧 AB 测试结果与推全结果有些差异
- 新老笔记抢流量不是问题,问题是 AB 测试与推全后的 设定 不一致,导致 AB 测试的结果不准确
- 举例说明
Option 2
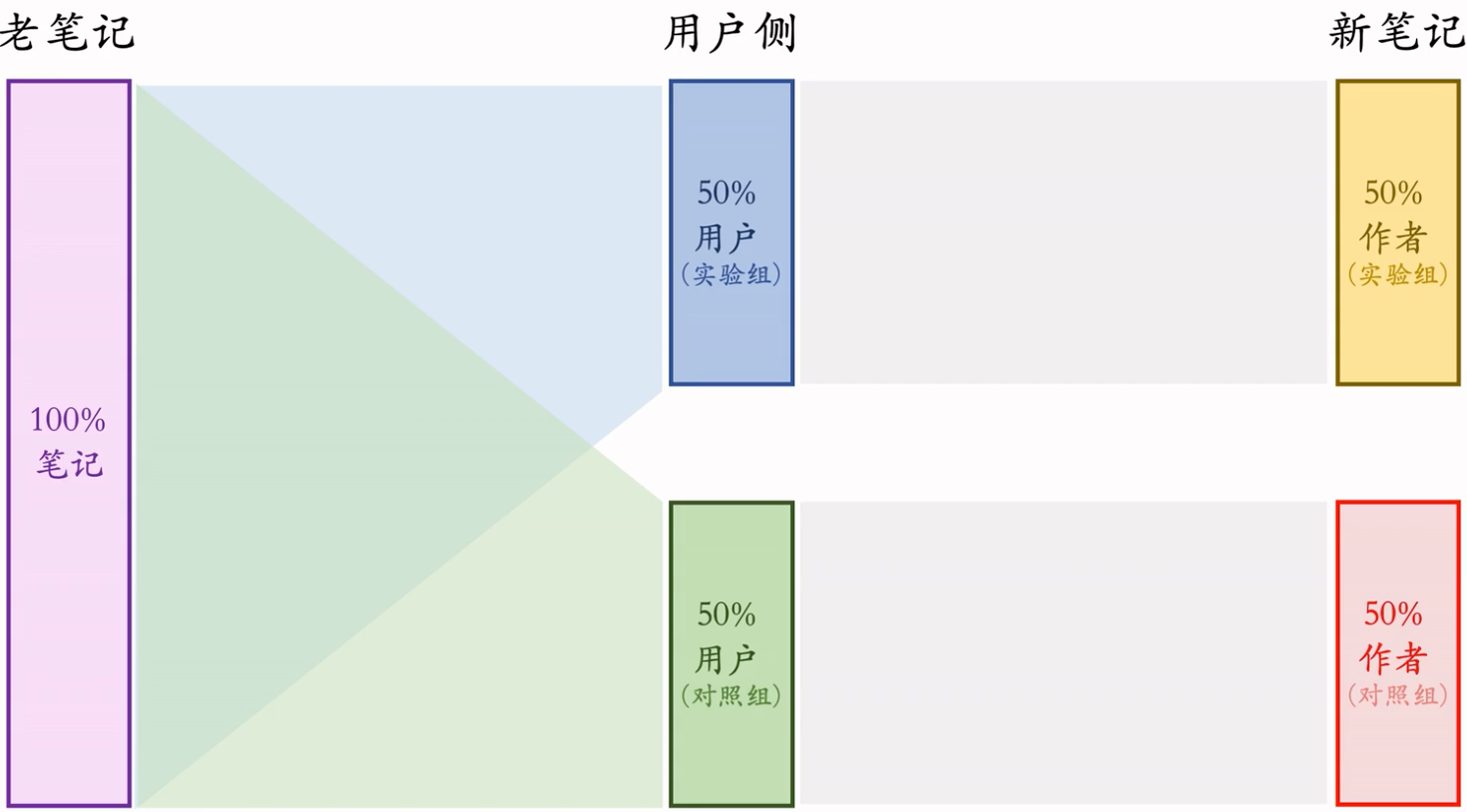
- 实验组用户只能看到实验组新笔记,对照组用户同理
- 这样就避免了两组新笔记抢流量
- 方案二比方案一的优缺点
- 优点:新笔记的两个桶不抢流量,作者侧实验结果更可信
- 相同:新笔记和老笔记抢流量,作者侧 AB 测试结果与推全结果有些差异
- 依然是 AB 测试时 50% 新笔记跟 100% 老笔记抢流量,推全后 100% 新笔记跟 100% 老笔记抢流量
- 缺点:新笔记池减小一半,对用户体验造成负面影响。原来100篇最好的,现在只剩50篇,还有再凑上50%没那么好的,会因为A/B test影响业务大盘,造成损失。
Option 3
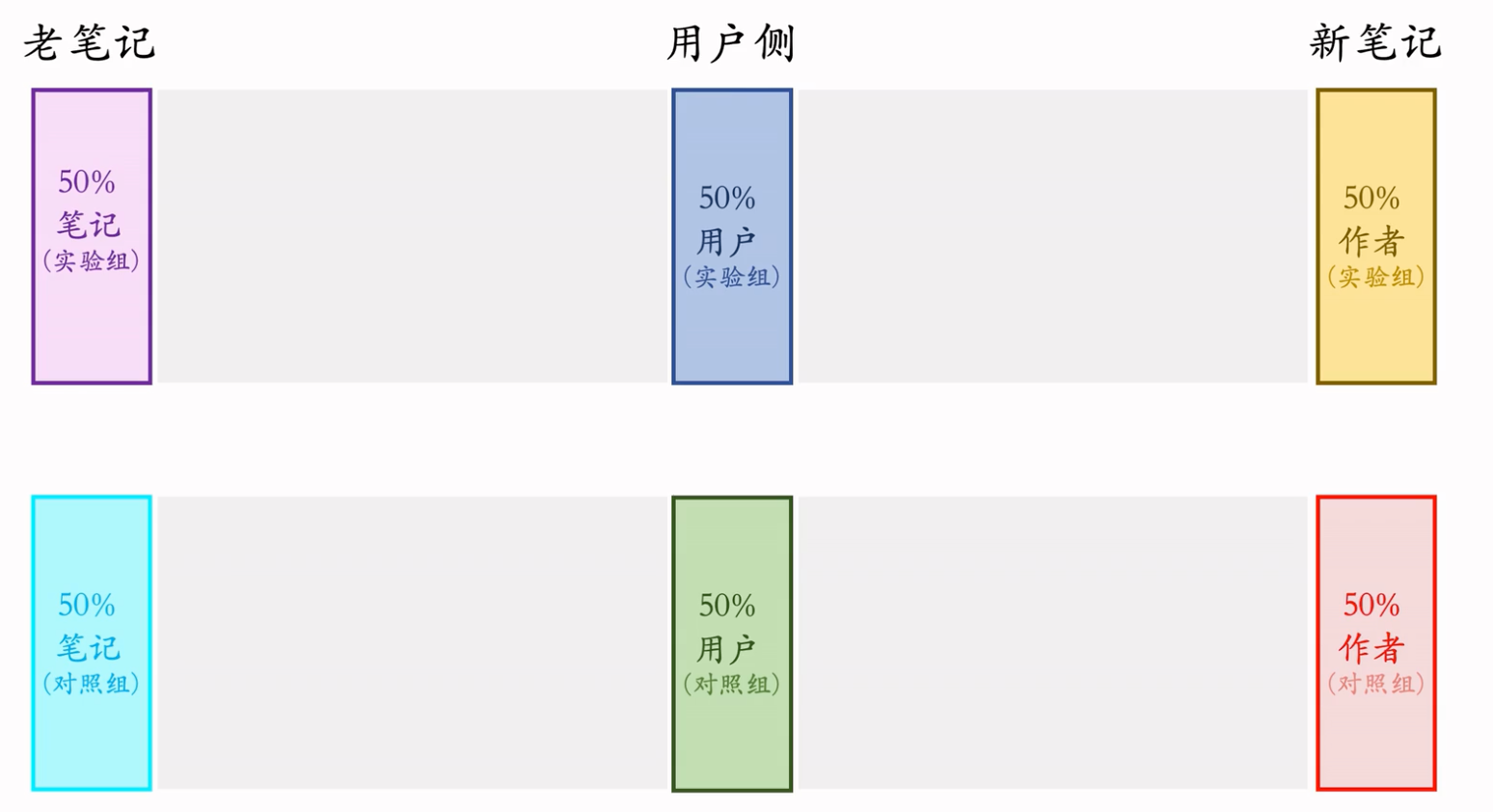
相当于把小红书切成了 2 个 APP。
这样做的实验结果是最精准的。
内容池少了一半,不太可行,太损害用户体验了:但是跨国 APP 可以用这个方案。
Summary
- 冷启的 AB 测试需要观测 作者发布指标 和 用户消费指标。
- 各种 AB 测试的方案都有缺陷(小红书有更好的方案,但也不完美)
- 设计方案的时候,问自己几个问题:
- 实验组、对照组新笔记会不会抢流量?
- 新笔记、老笔记怎么抢流量?AB 测试时怎么抢?推全后怎么抢?
- 同时隔离笔记、用户,会不会让内容池变小?
- 如果对新笔记做保量,会发生什么?
Indicator Growth Skills
Introduction
核心评价指标
- DAU和留存是最核心的指标,电商不太一样,营收是最核心的指标。
- 目前工业界最常用LT7和LT30衡量留存
- 某用户今天(t0)登录APP,未来7天(t0~t6)中有4天,登录APP,那么该用户今天(t0)的LT7等于4。
- 显然有1≤LT7≤7和1≤LT30≤30。
- 算法工程师最重要的目标就是提升LT,LT增长一般都意味着用户体验的提升。(除非LT增长而DAU下降,这意味着策略赶走了不活跃的用户,不好!)
- 假设APP禁止低活用户登录,则DAU下降,LT增长。
- 其他核心指标:用户使用时长、总阅读数(即总,点击数)、总曝光数。这些指标的重要性低于DAU和留存。
- 时长增长通常和LT是正相关的,时长提升了,LT通常也会提升。
- 时长增长,阅读数、曝光数可能会下降。比如抖音长视频增多,短视频减少。总时长增加,曝光数减少。
- 时长关系到DAU和留存,曝光影响到广告收入,需要平衡。
- 非核心指标:点击率、交互率、等等。核心上涨就行,不核心在核心上涨的情况下,下跌也没关系。
- 对于UGC平台,发布量和发布渗透率也是核心指标。
涨指标的方法:
- 改进召回模型,添加新的召回模型。
- 改进粗排和精排模型。
- 提升召回、粗排、精排中的多样性。
- 特殊对待新用户、低活用户等特殊人群。
- 利用关注、转发、评论这三种交互行为。
前两部分很详细,有公开资料,但是后面的三个都是工业界的实际经验,不好获取。其他公开渠道也很难找到。
Recall
推荐系统有几十条召回通道,它们的召回总量是固定的。总量越大,指标越好,粗排计算量越大。如果总量为5000,那这5000要给几十条召回通道分配。
双塔模型 (two-tower)和item-to-item (I2I)是最重要的两类召回模型,占据召回的大部分配额。有很多小众的模型,占据的配额很少。在召回总量不变的前提下,添加某些召回模型可以提升核心指标。这些模型的添加,不影响粗排的计算量,但是会挤兑别的模型的配额。
有很多内容池,比如30天物品、1天物品、6小时物品、新用户优质内容池、分人群内容池。后面会讲为啥需要这么多内容池。同一个模型可以用于多个内容池,得到多条召回通道。例如:只训练一个双塔模型,可以用在三个内容池上,得到三条召回通道,每条召回通道都有一定的配额。无论多少个内容池,都只训练一个双塔,不会增加训练的计算量。但是每个内容池都需要一个N索引,还需要线上做N检索,增加少量的计算成本。
双塔模型
方向1:优化正样本、负样本
- 简单正样本:有点击的(用户,物品)二元组。
- 简单负样本:随机组合的(用户,物品)二元组。
- 困难负样本:排序靠后的(用户,物品)二元组。被召回说明有些兴趣,排序被淘汰,则说明用户对这个物品的兴趣不大,可以作为负样本。
方向2:改进神经网络结构
Baseline:用户塔、物品塔分别是全连接网络,各输出一个向量,分别作为用户、物品的表征。
改进:用户塔、物品塔分别用DCN代替全连接网络。
改进:在用户塔中使用用户行为序列(last-n)。
改进:使用多向量模型代替单向量模型。(标准的双塔模型也叫单向量模型。)
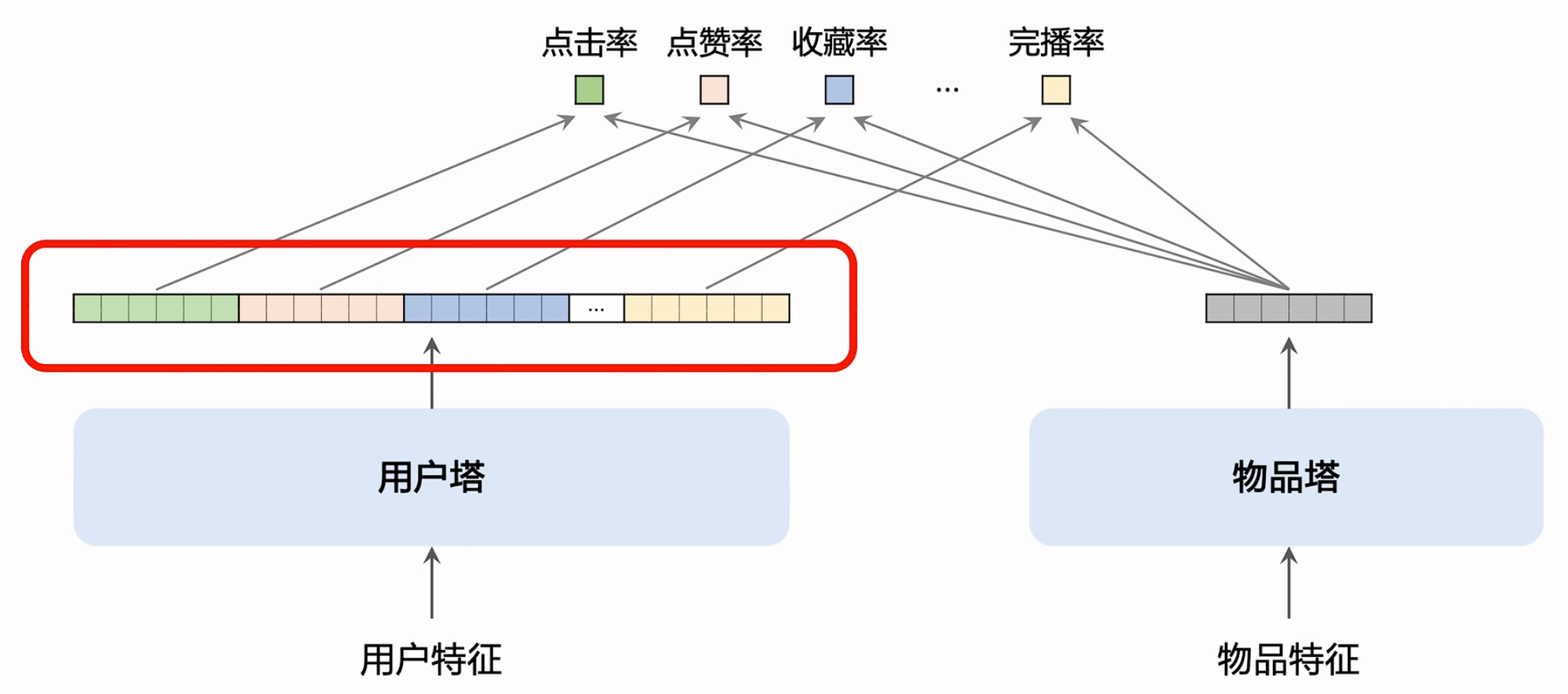
- 物品塔是一样的,只输出一个向量。用户塔会生成多个向量,每个向量的形状和物品塔输出的向量一致,就可以和物品塔的输出,算出很多的指标。有多少个指标,用户塔就会输出多少个向量。
- Why一个物品,多个用户?用户少,物品多,离线算出来存进向量数据库,如果每个指标,物品都要生成一个向量的话,存入对应的向量数据库的话,代价太大了(计算倍乘、存储也倍乘、向量数据库倍乘)。
方向3:改进模型的训练方法
- Baseline:做二分类,让模型学会区分正样本和负样本。
- 改进:结合二分类、batch内负采样。(对于batch内负采样,需要做纠偏。)
- 改进:使用自监督学习方法,让冷门物品的embedding学得更好。
Item-to-Item (I2I)
- 几乎和双塔同样重要,但是已经非常成熟了,能做的改进不太多。
- I2I是一大类模型,基于相似物品做召回。
- 最常见的用法是U2I2I(user>item>item)。
- 用户u喜欢物品i1(用户历史上交互过的物品)。
- 寻找i1的相似物品i2(即I2I)
- 将i2推荐给u
- 方法1:ItemCF及其变体。
- 一些用户同时喜欢物品i1和i2,则认为i1和i2相似。
- ItemCF、Online ItemCF、Swing、Online Swing都是基于相同的思想,只不过细节有些区别。
- 四种模型的结果存在足够大的差异,所以结合起来效果更好。同时用四种比只有一两种的效果更好。
- 线上同时使用上述4种I2I模型,各分配一定配额,各自的配额需要好好调一下。
- 方法2:基于物品向量表征,计算向量相似度。(双塔模型、图神经网络均可计算物品向量表征。)
小众的召回模型:
类似I2I的模型
- U2U2I(user -> user -> item):已知用户u1与u2相似,且u2喜欢物品i, 那么给用户u1推荐物品i。
- U2A2I(user -> author -> item):已知用户u喜欢作者a,
且a发布物品i,那么给用户u推荐物品i。 - U2A2A2I(user -> author -> author -> item):已知用户u喜欢作者a1,且a1与a2相似(不一定喜欢或者关注了a2),a2发布物品i,那么给用户u推荐物品i。
更复杂的模型:
- Path-based Deep Network (PDN)[1]
- Deep Retrieval [2]
- Sparse-Interest Network (SINE)[3]
- Multi-task Multi-view Graph Representation Learning (M2GRL)[4]
参考文献:
- Li et al.Path-based Deep Network for Candidate Item Matching in Recommenders.In S/G/R,2021
- Gao et al.Learning an end-to-end structure for retrieval in large-scale recommendations.In C/KM, 2021.
- Tan et al.Sparse-interest network for sequential recommendation.InWSDM,2021.
- Wang et al.M2GRL:A multitask multi-view graph representation learning framework for web-scale recommender systems.In KDD,2020.
工业界实践起来确实都有效,配额都很小,但是确实都有效果。召回总量不变的情况下,添加一些这样的通道,可以涨大盘指标!
总结:改进召回模型
- 双塔模型:优化正负样本、改进神经网络结构、改进训练的方法。
- I2I模型:同时使用ItemCF及其变体、使用物品向量表征计算物品相似度。
- 添加小众的召回模型,比如PDN、Deep Retrieval、SINB、M2GRL等模型。
- 在召回总量不变的前提下,仔细调整不同召回通道的配额,可以提升核心指标。(甚至可以让各用户群体用不同的配额。比如新用户和普通用户这两个群体)
- 增加召回总量显然可以提升指标,召回越多,粗排计算量越大。召回总量大到一定程度的时候,继续增加召回总量的边际效益会很小,ROI不划算。在s
Sort
Fine Ranking
精排模型的大致结构:
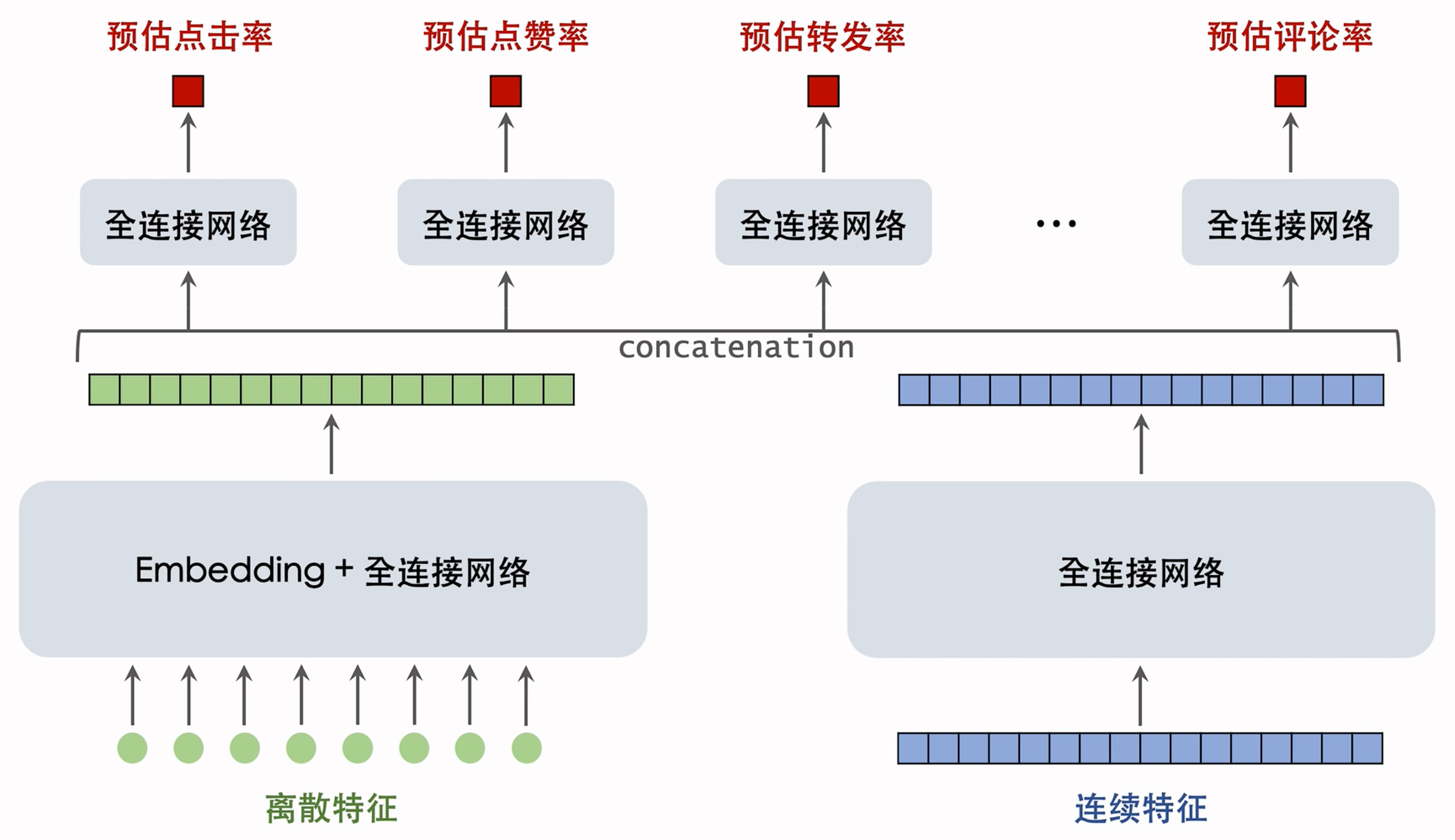
模型介绍:
输入大致可以分为:离散特征和连续特征。
- 离散特征:神经网络用Embedding层把离散特征映射到数值向量,把得到的数值向量拼接起来,得到一个几千维度的向量。再经过几个全连接层,得到一个大小是几百维的向量(上面绿色的)
- 连续特征:连续特种不多,也就是几百个(上面蓝色的)。蓝色神经网络是输入是个几百维的向量,输出也是个几百维的向量。
算力限制,下面这俩神经网络都不会很大。CPU推理的话,算力不够,下面这里全连接网络很小,基本只有1-2层,GPU推理能力更强,一般可以有3-6层。绿色/蓝色的向量做concatenation,作为更上层的神经网络的输入。基座:
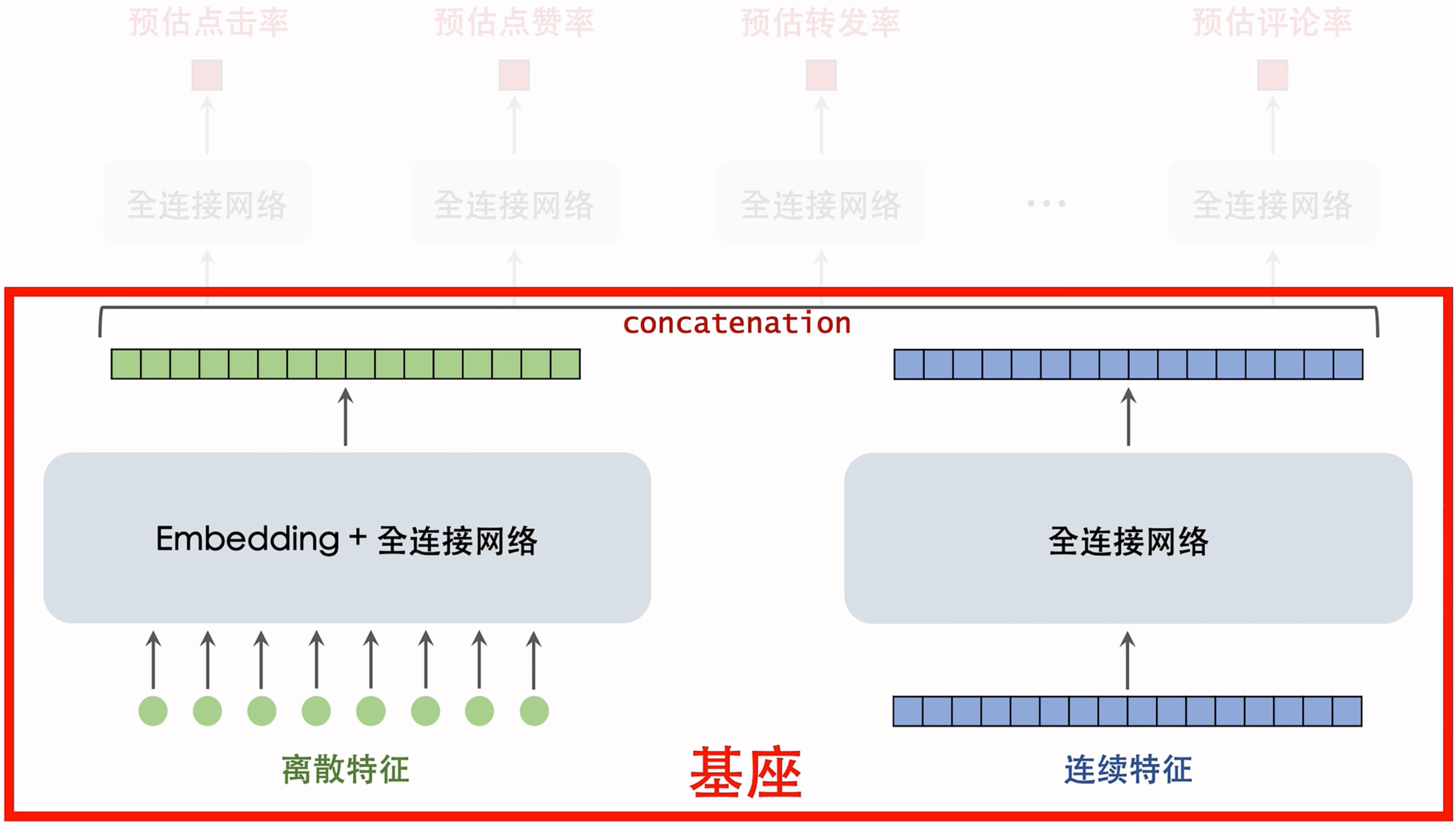
基座的作用就是把原始特征映射到数值向量。
concetenation后的结果会同时输入到多个全连接网络
- 这些网络一般只有两层。
- 这些网络的输出都是介于0到1之间的数值,作为各种目标的预估,比如预告点击率,点赞率,转发率,评论率等。
- 精排模型的基座和上面的多目标预估都有很多可以改进的点。
基座:
- 基座的输入包括离散特征和连续特征,输出一个向量,作为多目标预估的输入。
- 改进1:基座加宽加深,计算量更大,预测更准确。
- 精排模型的网络不够大,通常会underfit,推荐系统的参数亮很大的,通常有千亿/万亿,99%都在Embedding层,全连接参数量都很小。数据量太大,但是全连接网络不够大,加宽加深就会让预测更准。
- 加宽加深计算量也会加大,这就有ROI的问题了。
- 工业界常用的也就1-6层,取决于训练和推理的架构水平。算力强/架构先进,就可以6层,否则可能就1-2层。
- 改进2:做自动的特征交叉,比如Bilinear[1]和LHUC[2]。
- 参考文献:
- 1.Huang et al.FiBiNET:combining feature importance and bilinear feature interaction
for click-through rate prediction.In RecSys,2019. - 2.Swietojanski et al.Learning hidden unit contributions for unsupervised acoustic model adaptation.In WSDM,2016.
- 1.Huang et al.FiBiNET:combining feature importance and bilinear feature interaction
- 特征交叉实际用起来确实可以涨指标。
- 参考文献:
- 改进3:特征工程,比如添加统计特征、多模态内容特征。需要算法工程师根据自己的经验设计特征,判断哪些特征对预估有用,哪些特征可以做交叉。
多目标预估:
- 基于基座输出的向量,同时预估,点击率等多个目标
- 改进1:增加新的预估目标,并把预估结果加入融合公式。
- 最标准的目标包括,点击率、点赞率、收藏率、转发率、评论率、关注率、完播率…
- 寻找更多目标,比如进入评论区、给他人写的评论,点赞…
- 把新的预估目标加入融合公式,排序的时候会用到这些新的目标。算法工程师会寻找用户兴趣相关的目标,添加这样的目标可以提升留存等指标。
- 改进2:MMoE、PLE等结构可能有效,但往往无效。根据老师的经验,有些公司这样做涨了指标,但很多人试了都没有收益,无效的话不用感到惊讶。
- 改进3:纠正position bias,可能有效,但无效的可能性更大。老师的经验,观察到的数据有很强的position bias,但是很多同事花了很多精力去做也没啥用。
上面的精排方法,很多可以用于粗排,例如自动特征交叉,人工特征工程,还有增加新的预估目标等。
Coarse Ranking
- 粗排的打分量比精排大10倍(这样才能形成漏斗),因此粗排模型必须够快。大分量 x 10,那么单个物品的计算量就要 / 10,避免消耗太大的算力。
- 粗排不用和精排一样准确,因此简单点可以:
- 简单模型:多向量双塔模型,同时预估点击率等多个目标。
- 复杂模型:三塔模型效果好,但工程实现难度较大。
- 粗精排一致性建模
- 蒸馏精排训练粗排,让粗排与精排更一致。
- 方法1:pointwise蒸馏
- 设y是用户真实行为,设p是精排的预估·
- 用$\frac{y+p}{2}$作为粗排拟合的目标。不用蒸馏的话,训练直接用y作为目标,但是用均值比直接用y效果更好哦!
- 例:
- 对于点击率目标,用户有点击(y=1),精排预估p=0.6。
- 用$\frac{y+p}{2}=0.8$作为粗排拟合的点击率目标。
- 方法2:pairwise或listwise蒸馏
- 给定k个候选物品,按照精排预估做排序。
- 做learning to rank(LTR),让粗排拟合物品的序(而非具体的点击率数值)
- 例:
- 对于物品i和j,精排预估点击率为$p_i>p_j$
- LTR鼓励粗排预估点击率满足$q_i > q_j$,否则有惩罚
- LTR通常使用pairwise logistic loss作为损失函数
- 优点:粗精排一致性建模可以提升核心指标,效果十分显著。做简单的pointwist蒸馏效果就很好了,大厂会用更复杂的pairwise/listwist。
- 缺点:用精排蒸馏粗排有缺点,系统很大很杂,如果精排出bug(很多时候bug造成的指标缓慢下降,还很难感知到),精排预估值p有偏,会污染粗排训练数据,让粗排也逐渐变差,而且不容易被察觉到。
User Behavior Sequence Modeling
排序到头了越来越难了,这时候涨指标最重要的途径就是用户行为建模
- 用户行为序列建模(前面都讲过)
- 最简单的方法是对物品向量取平均,作为一种用户特征。
- DIN 使用注意力机制,对物品向量做加权平均。
- 工业界目前沿着SIM的方向发展。先用类目等属性筛选物品,然后用DIN对物品向量做加权平均。
参考文献
- Covington,Adams,and Sargin.Deep neural networks for YouTube recommendations. In RecSys,2016.
- Zhou et al.Deep interest network for click-through rate prediction.In KDD,2018.
- Qi et al.Search-based User Interest Modeling with Lifelong Sequential Behavior Data for Click-Through Rate Prediction.In CIKM,2020.
- 改进方向:
- 改进1:增加序列长度,让预测更准确,但是会增加计算成本和推理时间。难点是工程架构,工程架构弱做不到长序列。现在长序列建模做的最好的是快手,超长序列建模可以使用100w+个物品,几乎可以覆盖用户历史上的全部行为。非常难!!!算法原理简单,但是鸡架不行的话,扛不住。序列长度很长靠的还是工程架构哈!
- 改进2:筛选的方法,比如用类目、物品向量表征聚类。100w+个全塞进去不符合实际,筛选一把!着重物品向量表征聚类:
- 离线用多模态神经网络提取物品内容特征,将物品表征为向量。用Bert或者Clip这样的模型。
- 离线将物品向量聚为1000类,每个物品有一个聚类序号。(聚类一般用层次聚类)
- 线上排序时,用户行为序列中有n=1,000,000个物品。某候选物品的聚类序号是70,对个物品做筛选,只保留聚类序号为70的物品。n个物品中只有数千个被保留下来。
- 同时有好几种筛选方法,取筛选结果的并集。
- 可能还要进一步筛选,让物品数量再降低一个数量级,然后再输入到注意力层。
- 改进3:对用户行为序列中的物品,使用ID以外的一些特征。
- 最简单就是ID做Embedding,作为物品的向量表征。
- 还可以再加一些别的物品特征,效果会更好。但是不能加太多,不然线上推理的时候,通信和计算都会出问题。
- 概括:沿着SIM的方向发展,让原始的序列尽量长,然后做筛选降低序列长度,最后将筛选结果输入DIN。
Online Learning
在线学习对于推荐系统的提升非常大,但是它会消耗更多的算力
既需要在凌晨做全量更新,也需要全天不间断做增量更新。
设在线学习需要10,000 CPU core的算力增量更新一个精排模型。推荐系统一共需要多少额外的算力给在线学习?
为了做AB测试,线上同时运行多个不同的模型。
如果线上有m个模型’则需要m套在线学习的机器。
线上有m个模型,其中1个是holdout,1个是推全的模型,m一2个测试的新模型。
以精排为例子:

holdout一个,推全一个,新模型俩,总共四套资源。推全和holdout的模型不一定一致,一般推全会新几个版本。而且要跑一段时间的,七日留存?三十日留存?资源会在一段时间内被占用。
同样的道理,召回和粗排也需要做在线学习。每个模型都需要一套计算资源。好在召回和粗排的模型小,资源需要的少一些。
总结:
- 线上有m个模型,其中1个是holdout,1个是推全的模型,m一2个测试的新模型。
- 每套在线学习的机器成本都很大,因此m数量很小,制约模型开发迭代的效率。
- 在线学习对指标的提升巨大,但是会制约模型开发迭代的效率。最好在模型相对成熟之后再考虑在线学习,过早在线学习容易把模型锁死在较弱的版本,后续迭代会很慢。
Old Soup Model
算法工程师遇到的最麻烦的一个问题,解决不了的话,新模型很难超过老模型。
老汤模型是啥?
“老汤模型”这个术语用来描述在推荐系统中,一个已经经过长时间训练和更新的模型,它已经积累了大量的数据和经验,因此很难被新模型超越,即使新模型在理论上可能更先进 。这种现象在模型更新和比较时需要特别注意,以确保公平性 。
用每天新产生的数据对模型做1 epoch的训练。
久而久之,老模型训练得非常好,很难被超过。
对模型做改进’重新训练’很难追上老模型…
问题:
- 问题1:如何快速判断新模型结构是否优于老模型?(不需要追上线上的老模型,只需要判断新老模型谁的结构更优。)
- 问题2:如何更快追平、超过线上的老模型?(只有几十天的数据,新模型就能追上训练上百天的老模型。)
问题一解决方案:
- 核心思想:“拉回同一起跑线”
- 对于新、老模型结构,都随机初始化模型全连接层。
- Embedding层可以是随机初始化,也可以是复用老模型训练好的参数。
- 用n天的数据训练新老模型。(从旧到新,训练1 epoch)。
- 如果新模型显著优于老模型,新模型很可能更优。
- 只是比较新老模型结构谁更好,而非真正追平老模型。
问题二解决方案:
- 已经得出初步结论,认为新模型很可能优于老模型。用几十天的数据训练新模型’早日追平老模型。
- 方法1:尽可能多地复用老模型训练好的embedding层,避免随机初始化embedding层。(Embedding层是对用户、物品特点的“记忆”,比全连接层学得慢。)
- 方法2:用老模型做teacher,蒸馏新模型。(用户真实行为是y,老模型的预测是p,用$\frac{y+p}{2}$作为训练新模型的目标。)在训练新模型的初期,做蒸馏,可以大幅增加收敛,让新模型追的更快。
Summary
- 精排模型:改进模型基座(加宽加深、特征交叉、特征工程),改进多目标预估(增加新目标、MMoE、position bias)。并非都有效,做了实验才知道。
- 粗排模型:更好的模型结构,例如三塔模型(取代多向量双塔模型),粗精排一致性建模。
- 用户行为序列建模:沿着SIM的方向迭代升级,加长序列长度,改进筛选物品的方法。
- 在线学习:对指标提升大,但是会降低模型迭代升级效率。
- 老汤模型制约模型迭代升级效率,需要特殊技巧。
Diversity
Diversity in Fine Ranking
- 精排阶段,结合兴趣分数和多样性分数对物品$i$排序。
- $s_i$: 兴趣分数,即融合点击率等多个预估目标的分数。
- $d_i$: 多样性分数,即物品$i$和已经选中的物品的差异。
- 用$s_{i} + d_{i}$对物品做排序,这个排序几乎决定了最终用户看到的推荐结果。
- 常用MMR、DPP等方法计算多样性分数,精排使用滑动窗口,粗排不使用滑动窗口。
- 精排决定最终的曝光,曝光页面上邻近的物品相似度应该小。所以计算精排多样性要使用滑动窗口。
- 例如:一个物品要和前五个物品有很大的差异,如果相似物品离得太近,就会影响用户体验。所以计算精排多样的时候,要使用滑动窗口,保证同一个滑动窗口内的物品要有足够大的差异。
- 粗排不决定最终曝光,只是给精排提供候选。粗排要考虑整体的多样性,而非一个滑动窗口中的多样性。
- 除了多样性分数,精排还使用打散策略增加多样性。
- 类目:当前选中物品$i$,之后5个位置不允许跟$i$的二级类目相同。
- 多模态:事先计算物品多模态内容向量表征,将全库物品聚为1000类;在精排阶段,如果当前选中物品$i$,之后10个位置不允许跟$i$同属一个聚类。道理:同一个聚类中的物品的图片和文字相似,应该被打散。
Diversity in Coarse Ranking
也很重要
- 粗排给5000个物品打分,选出500个物品送入精排。提示这500个多样性有助于提升推荐系统核心指标,提升粗排和精排多样性都可以提升推荐系统核心指标。
- 根据$s_i$对5000个物品排序,分数最高的200个物品送入
精排。(优先考虑兴趣分数,不可虑多样性分数,保证用户最感兴趣的物品可以进入精排) - 对于剩余的4800个物品,对每个物品$i$计算兴趣分数$s_i$和多样性分数$d_i$,根据$s_i + d_i$,对于剩下4800个物品排序,分数最高的300个送入精排。(既是用户比较感兴趣的,也跟已经选中的物品有较大的差异,保证了多样性。)
Diversity in Recall
双塔模型:添加噪声
- 双塔模型是最重要的召回模型,占的召回名额最多。
- 用户塔将用户特征作为输入,输出用户的向量表征;然后做ANN检索,召回向量相似度高的物品。
- 线上做召回时(在计算出用户向量之后,在做ANN检索之前),往用户向量中添加随机噪声(比如随机高斯噪声就行)。线上真有利于推荐系统核心指标!!!
- 噪声多强取决于用户的兴趣,用户的兴趣越窄(比如用户最近交互的个物品只覆盖少数几个类目),则添加的噪声越强。可以拿用户最后交互过的n个物品,来衡量用户的兴趣宽窄。
- 添加噪声让召回变得“不准”,但是添加噪声确实使得召回的物品更多样,可以提升推荐系统核心指标。
双塔模型:抽样用户行为序列
- 用户最近交互的n个物品(用户行为序列),是用户塔的输入。保留最近的r个物品(r << n)。
- 从剩余的n一T个物品中随机抽样t个物品(t << n)。(可以是均匀抽样,也可以用非均匀抽样让类目平衡)
- 将得到的r+t个物品作为用户行为序列,而不是用全部个物品。(具有随机性和差异,多样性up)
- 抽样用户行为序列为什么能涨指标?
- 一方面,注入随机性,召回结果更多样化。
- 另一方面,可以非常大,可以利用到用户很久之前的兴趣。
- 概括一下:提升多样性 + 捕捉更久之前的兴趣点,提升指标。
U2I2I:抽样用户行为序列
- U212 (user→item→item) 中的第一个item是指用户最近交互的n个物品之一,在U2I2I中叫作种子物品。
- N个物品覆盖的类目数较少,且类目不平衡。
- e.g. 系统共有200个类目,某用户的个物品只覆盖15个类目。用户兴趣不是很宽泛。
- e.g. 足球类目的物品有0.4n个,电视剧类目的物品有0.2n个,其余类目的物品数均少于0.05n个。
- 用这些种子召回出来的结果,也具有类目较少且不平衡的特性。
- 做非均匀随机抽样,从个物品中选出t个,让类目平衡。(想法和效果与双塔中的用户行为序列抽样相似。)用抽样得到的t个物品(代替原本的n个物品)作为U2I2I的种子物品。这样召回的结果会更多样一些。
- 可以提升指标!!!Reason:
- 一方面,抽样可以让类目更平衡,多样性更好。
- 另一方面,n可以更大(因为只从中抽一个子集出来做输入),覆盖的类目数量会大很多,多样性会更好。
探索流量
- 每个用户曝光的物品中有2%是非个性化的,用作兴趣探索。
- 维护一个精选内容池,其中物品均为交互率指标高的优质物品。(内容池可以分人群,比如30~40岁男性内容池,专门推荐给30~40岁男性用户)
- 为什么要精选内容池?没有个性化 -> 提高物品质量,要通过提高质量来弥补缺少个性化带来的损失。
- 从精选内容池中随机抽样几个物品,跳过排序,直接插入最终排序结果。没办法对这样的物品做公平的排序,这样的物品不匹配用户过去的兴趣点,大概率会被排序模型给淘汰掉。所以只能做提权或者强插。
- 兴趣探索一定会在短期内负向影响核心指标,但长期会产生正向影响。道理很显然:非个性化推荐用户大概率不感兴趣,点击率偏低用户不看。2%的流量大部分会被浪费掉,但是长期有利,可以发觉用户的兴趣点,更好吸引用户留存。
总结:
- 精排:结合兴趣分数和多样性分数做排序;做规则打散·
- 粗排:只用兴趣分数选出部分物品;结合兴趣分数和多样性分数选出部分物品。
- 召回:往双搭模型的用户向量添加噪声;对用户行为序列做非均匀随机抽样(对双塔和U2I2I都适用)
- 兴趣探索:保留少部分的流量给非个性化推荐。长期有好处。
Special treatment for special groups
Why
- 新用户、低活用户的行为很少,个性化推荐不准确。
- 新用户、低活用户容易流失,要想办法促使他们留存。指标有区别,特殊策略。
- 全体用户,很多指标:留存,时长,阅读,消费。。。
- 新用户/低活用户:留存,不用考虑别的。留下来先。
- 特殊用户的行为(比如点击率、交互率)不同于主流用户,基于全体用户行为训练出的模型在特殊用户人群上有偏。
涨指标的方法
- 构造特殊内容池,用于特殊用户人群的召回。
- 使用特殊排序策略,保护特殊用户。
- 使用特殊的排序模型,消除模型预估的偏差。
构造特殊的内容池
- why
- 新用户、低活用户的行为很少,个性化召回不准确。(既然个性化不好,那么就保证内容质量好。优质内容弥补个性化的缺失)
- 针对特定人群的特点构造特殊内容池,提升用户满意度。(例如,对于喜欢留评论的中年女性,构造促评论内容池,满足这些用户的互动需求。)
- how
- 方法1:根据物品获得的交互次数、交互率选择优质物品。
- 圈定人群:只考虑特定人群,例如18~25岁一二线城市男性。
- 构造内容池:用该人群对物品的交互次数、交互率给物品打分,选出分数最高的物品进入内容池.
- 内容池有弱个性化的效果。
- 内容池定期更新,加入新物品,排除交互率低和失去时效性的老物品。
- 该内容池只对该人群生效。
- 方法2:做因果推断,判断物品对人群留存率的贡献,根据贡献值选物品。(工业界已经在用了,但是技术还是不算成熟。)
- 方法1:根据物品获得的交互次数、交互率选择优质物品。
- why
特殊内容池的召回
- 通常使用双塔模型从特殊内容池中做召回
- 双塔模型是个性化的
- 对于新用户,双塔模型的个性化做不准。
- 靠高质量内容、弱个性化做弥补。容忍双塔的不准确。
- 额外的训练代价?
- 对于正常用户,不论有多少内容池,只训练一个双塔模型。
- 对于新用户,由于历史交互记录很少,需要单独训练模型。
- 额外的推理代价?
- 内容池定期更新,然后要更新ANN索引。
- 线上做召回时,需要做ANN检索。(少量的算力),每多一个内容池,都要多一份算力,内容池越大需要的算力也就越大。
- 特殊内容池都很小(比全量内容池小10~100倍),所以需要的额外算力不大。
- 通常使用双塔模型从特殊内容池中做召回
特殊的排序策略
- 对于新用户、低活用户这样的特殊人群,业务上只关注留存,不在乎消费(总曝光量、广告收入、电商收入)
- 对于新用户、低活用户,少出广告、甚至不出广告。
- 新发布的物品不在新用户、低活用户上做探索。
- 物品新发布时,推荐做得不准,会损害用户体验。
- 只在活跃的老用户上做探索,对新物品提权(boost)。
- 不在新用户、低活用户上做探索,避免伤害用户体验。
差异化的融分公式
- 新用户、低活用户的,点击、交互行为不同于正常用户。
- 低活用户的人均点击量很小;没有点击就不会有进一步的交互。
- 低活用户的融分公式中,提高预估点击率的权重(相较于普通用户),降低交互率的权重。这样更容易促使低活用户点击物品,点进去看了才有可能留存。
- 保留几个曝光坑位给预估点击率最高的几个物品。
- 例:精排从500个物品中选50个作为推荐结果,其中3个坑位给点击率最高的物品(吸引用户点击),剩余47个坑位由融分公式决定。
- 甚至可以把,点击率最高的物品排在第一,确保用户一定能看到。(大厂实验结论:确实可以提高用户留存,有效!只对低活人群生效,用在活跃用户身上则会损害指标。)
特殊的排序模型
特殊用户人群的行为不同于普通用户。新用户、低活用户的,点击率、交互率偏高或偏低。
排序模型被主流用户主导,对特殊用户做不准预估。
- 用全体用户数据训练出的模型,给新用户做的预估有严重偏差。
- 如果一个APP的用90%是女性,用全体用户数据训练出的模型,对男性用户做的预估有偏差。
问题:对于特殊用户,如何让排序模型预估做得准?
差异化的排序模型:
- 方法1:大模型+小模型
- 用全体用户行为训练大模型,大模型的预估拟合用户行为y。
- 用特殊用户的行为训练小模型,小模型的预估q,拟合大模型的残差y-p。希望小模型纠正大模型犯的错误。
- 对主流用尸只用大模型做预估p。
- 对特殊用户,结合大模型和小模型的预估
p + q,小模型起到纠偏的作用。
- 方法2:融合多个experts,类似MMoE。
- 只用一个模型,模型有多个experts,各输出一个向量。
- 对experts的输出做加权平均,得到一个向量。
- 和MMOE的不同:MMOE有一个小神经网络,全部特征作为输入,输出是experts的权重。这里的区别:根据用户特征计算权重,不用其他的特征。由用户特征决定experts的权重。
- 以新用户为例,模型将用户的新老、活跃度等特征作为输入,输出权重,用于对experts做加权平均。
- 方法3:大模型预估之后,用小模型做校准。
- 用大模型预估点击率、交互率。大模型大量数据,在全体数据上进行训练得到的,对于大量活跃用户比较准。
- 将用户特征、大模型预估,点击率和交互率作为小模型(例如GBDT)的输入。
- 在特殊用户人群的数据上训练小模型,小模型的输出拟合用户真实行为。
- 这里的小模型:结合大模型的预估和用户特征特征,小模型再做一次预估,起到校准的作用。
- 特殊人群上,小模型的预估比大模型更加准确。直接就用小模型的预估了!
- 注意方法1、3的区别:一个是校准,一个是纠偏。一个是并行,两个一起使用,结合起来作为最终结果。一个是串行,先小后大,作为结果。
- 方法1:大模型+小模型
错误的做法
- 每个用户人群使用一个排序模型,推荐系统同时维护多个大模型。
- 系统有一个主模型;每个用户人群有自己的一个模型。
- 每天凌晨,用全体用户数据更新主模型。
- 基于训练好的主模型,在某特殊用户人群的数据上再训练 1 epoch,作为该用户人群的模型。
- 短期可以提升指标;维护代价大’长期有害。
- 起初,低活男性用户模型比主模型的AUC高0.2%。
- 主模型迭代几个版本后,AUC累计提升0.5%
- 特殊人群模型太多,长期没有人维护和更新。
- 如果把低活男性用户模型下线,换成主模型,在低活男性用户上的AUC反倒提升0.3%!
- 看似win-win,其实推荐系统前后没有任何改变啊,上线了又下线了这。。。浪费了人的时间和机器的算力,还不如直接弄主模型呢orz。
- 不建议让每个用户人群都有自己的排序模型,最好只有一个统一的模型,最多再加几个小模型,对主模型做纠偏和校准。
- 每个用户人群使用一个排序模型,推荐系统同时维护多个大模型。
总结:
- 召回:针对特殊用户人群,构造特殊的内容池,增加相应的召回通道。
- 排序策略:排除低质量物品,保护新用户和低活用户;特殊用户人群使用特殊的融分公式。
- 排序模型:结合大模型和小模型,小模型拟合大模型的残差;只用一个模型,模型有多个experts;大模型预估之后用小模型做校准。
Interactive behavior
利用关注、转发、评论这三种交互行为。
交互行为
- 交互行为:点赞、收藏、转发、关注、评论……
- 推荐系统如何利用交互行为?
- 最简单的方法:将模型预估的交互率用于排序。
- 模型将交互行为当做预估的目标。
- 将预估的点击率、交互率做融合,作为排序的依据。(工业界全会这么做)
- 其他用途?
关注(粉丝)
关注量对于留存的价值
对于一位用户,他关注的作者越多,则平台对他的吸引力越强。
用户留存率(r)与他关注的作者数量(f)正相关,但不是正比。
如果某用户的 f 较小,则推荐系统要促使该用户关注更多作者。
图像大致如下:
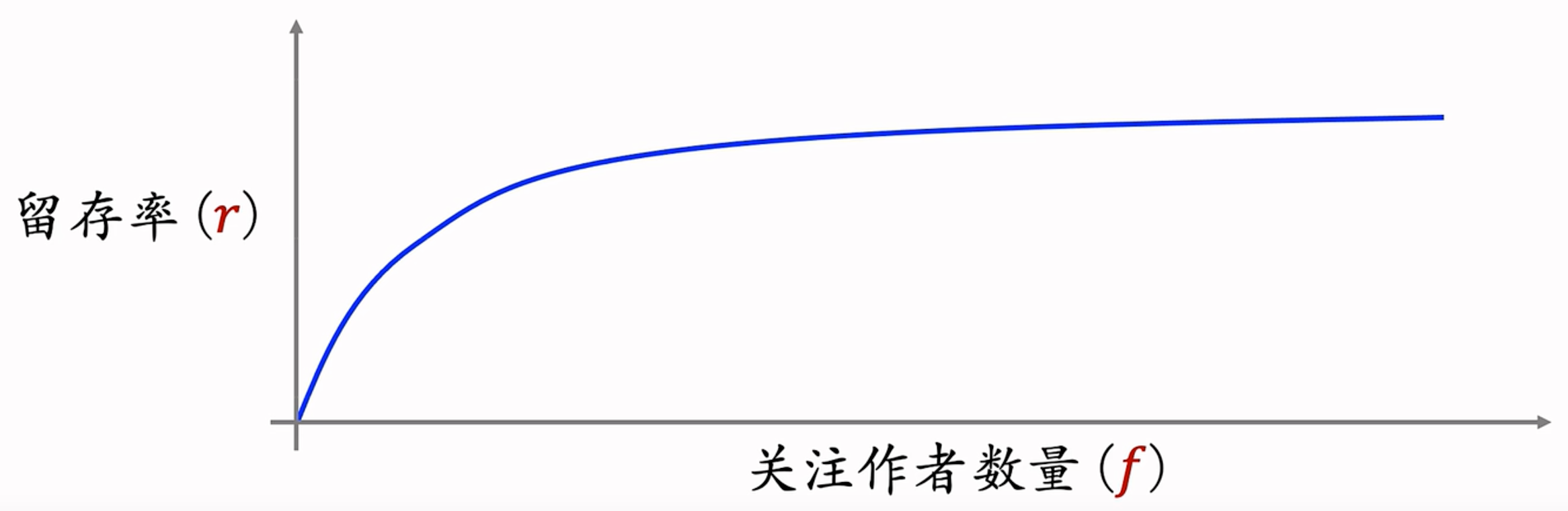
如何利用关注关系提升用户留存?
- 方法1:用排序策略提升关注量
- 对于用户u,模型预估候选物品$i$的关注率为$p_i$
- 设用户$u$已经关注了$f$个作者。
- 我们定义单调递减函数$w(f)$,用户已经关注的作者越多,则$w(f)$越小。
- 在排序融分公式中添加$w(f)·p_{i}$用于促关注(如果f小且$p_i$大,则$w(f)·p_{i}$给物品i带来很大加分,排序靠前)。反之,如果f很大,则$w(f)$会接近0,这一项乘积就不起作用了。只有f小的时候,排序策略才会起到促关注作用。
- 方法2:构造促关注内容池和召回通道
- 这个内容池中物品的关注率高,可以促关注。
- 如果用户关注的作者数f较小,则对该用户使用该内容池。
- 召回配额可以固定’也可以与f负相关。
- 方法1:用排序策略提升关注量
粉丝对于促发步的价值
- UGC平台将作者发布量、发布率作为核心指标,希望作者多发布。
- 作者发布的物品被平台推送给用户,会产生,点赞、评论、关注等交互。
- 交互(尤其是关注、评论)可以提升作者发布积极性。
- 作者的粉丝数越少,则每增加一个粉丝对发布积极性的提升越大(边际效应递减)。
- 用排序策略帮助低粉新作者涨粉。某作者a的粉丝数(被关注数)为$f_a$。作者α发布的物品i可能被推荐给用户u,模型预估关注率为$p_{ui}$。
- 我们定义单调递减函数$w(f_a)$作为权重,作者a的粉丝越多,则$w(f_a)$越小。在排序融分公式中添加$w(f_a)·p_{ui}$,帮助低粉作者涨粉,扶持一下,从而激发创作积极性。
隐式关注关系
- 召回通道U2A2I:user -> author -> item
- 显式关注关系:用户u关注了作者a,将a发布的物品推荐给u。(点击率、交互率指标通常高于其他召回通道。)
- 隐式关注关系:用户u喜欢看作者a发布的物品,但是u没有关注a。
- 隐式关注的作者数量远大于显式关注。挖掘隐式关注关系,构造U2A2I召回通道,可以提升推荐系统核心指标。
转发(分享)
- 促转发(分享回流)
- A平台用户将物品转发到B平台,可以为A吸引站外流量。
- 推荐系统做促转发(也叫分享回流)可以提升DAU和消费指标。
- 简单提升转发次数是否有效呢?
- 模型预估转发率为$p$,融分公式中有一项$w · p$,让转发率大的物品更容易获得曝光机会。
- 增大权重$w$可以促转发,吸引站外流量,但是会负面影响,点击率和其他交互率。
- KOL建模
- 目标:在不损害点击和其他交互的前提下,尽量多吸引站外流量。
- 什么样的用户的转发可以吸引大量站外流量?
- 答案:其他平台的Key Opinion Leader(KOL),也就是我们常说的大V。
- 用户u是我们站内的K○L,但他不是其他平台的KOL,他的转发价值大吗?No
- 用户在我们站内没有粉丝,但他是其他平台的KOL,他的转发价值大吗?Yes
- 如何判断本平台的用户是不是其他平台的KOL?该用户历史上的转发能带来多少站外流量。
- 促转发的策略:
- 目标:在不损害,点击和其他交互的前提下,尽量多吸引站外流量。
- 识别出的站外KOL之后,该如何用于排序和召回?
- 方法1:排序融分公式中添加额外的一项$k_u · p_{ui}$。
- $k_u$:如果用户u是站外KOL,则$k_u$大。
- $p_{ui}$:为用户u推荐物品i, 模型预估的转发率。
- 如果u是站外KOL,利用转发的价值,则多给他曝光他可能转发的物品,不知不觉中给平台多吸引站外流量。
- 如果u不是站外KOL,$k_u$接近于0,这一项总是接近于0。不会干扰排序融分公式。
- 总而言之:只影响少数用户,对于绝大多数用户没有影响。正式通过这些少数用户吸引站外流量,提升大盘指标。
- 方法2:构造促转发内容池和召回通道,对站外KOL生效。(和前面促关注的十分类似哈,不再重复)
- 方法1:排序融分公式中添加额外的一项$k_u · p_{ui}$。
- 促转发(分享回流)
评论
- 评论促发布
- UGC平台将作者发布量、发布率作为核心指标,希望作者多发布。
- 关注、评论等交互可以提升作者发布积极性。
- 如果新发布物品尚未获得很多评论,则给预估评论率提权,让物品尽快获得评论。反之,边际效益递减,就不用提权了。
- 排序融分公式中添加额外一项$W_i · P_i$。
- $W_i$:权重,与物品$i$已有的评论数量负相关。
- $P_i$:为用户推荐物品i,模型预估的评论率。
- 添加这个,评论少的时候,提权。评论多的时候就没啥影响了。
- 评论的其他价值:
- 有的用户喜欢留评论,喜欢跟作者、评论区用户互动。
- 给这样的用户添加促评论的内容池,让他们更多机会参与讨论。
- 有利于提升这些用户的留存。
- 有的用户常留高质量评论(评论的点赞量高)。
- 高质量评论对作者、其他用户的留存有贡献。(作者、其他用户觉得这样的评论有趣或有帮助)
- 用排序和召回策略鼓励这些用户多留评论。
- 有的用户喜欢留评论,喜欢跟作者、评论区用户互动。
- 评论促发布
总结
- 关注:留存价值(让新用户关注更多作者,提升新用户留存);发布价值(帮助新作者获得更多粉丝,提升作者发布积极性);利用隐式关注关系做召回。
- 转发:判断哪些用户是站外的KOL,利用他们转发的价值,吸引站外的流量。
- 评论:发布价值(促使新物品获得评论,提升作者发布积极性);留存价值(给喜欢讨论的用户创造更多留评机会);鼓励高质量评论的用户多留评论。
References
- Shusen Wang的公开课
- Shuseng Wang的笔记
- 同学对于Shuseng的课做的很全很全的笔记,参考了许多内容,很有价值!