算法岗面试汇总-1

这里汇总一下，算法岗相关的面经！参考自这个Github Repo，综合提纲和GPT，给出答案。

GPT Prompt

• 假设你是一位耐心、热心数据分析岗位岗位的mentor，你拥有丰富的微积分、线性代数、机器学习、深度学习知识，并且熟练掌握各种面试题和其答案。我作为一位刚入职的mentee，会询问你许多算法岗位的问题或疑问，请你用简洁易懂、高度概括的方式，根据我询问的问题，告诉我问题的答案。如果我的提问是列表，请你分别根据列表中的每个问题，进行回答。
• Local GPT deployment tutorial

Question Overview

1. 机器学习

1-1. 简述解决一个机器学习问题时，你的流程是怎样的？
1-2. 损失函数是什么，如何定义合理的损失函数？
1-3. 回归模型和分类模型常用损失函数有哪些？各有什么优缺点
1-4. 什么是结构误差和经验误差？训练模型的时候如何判断已经达到最优？
1-5. 模型的“泛化”能力是指？如何提升模型泛化能力？
1-6. 什么是混淆矩阵？
1-7. 如何选择合适的模型评估指标？AUC、精准度、召回率、F1值都是什么？如何计算？有什么优缺点？
1-8. ROC曲线如何绘制？相比P-R曲线有什么特点？
1-9. 如何评判模型是过拟合还是欠拟合？遇到过拟合或欠拟合时，你是如何解决？
1-10. 你是如何针对应用场景选择合适的模型？
1-11. 如何选择模型中的超参数？有什么方法，并说说其优劣点
1-12. 误差分析是什么？你是如何进行误差分析？
1-13. 你是如何理解模型的偏差和方差？什么样的情况是高偏差，什么情况是高方差？
1-14. 出现高偏差或者高方差的时候你有什么优化策略？
1-15. 奥卡姆剃刀定律是什么？对机器学习模型优化有何启发？举例说明
1-16. 线性模型和非线性模型的区别？哪些模型是线性模型，哪些模型是非线性模型？
1-17. 生成式模型和判别式模型的区别？哪些模型是生成式模型，哪些模型是判别式模型？
1-18. 概率模型和非概率模型的区别？哪些模型是概率模型，哪些模型是非概率模型？
1-19. 参数化模型和非参数化模型的区别？哪些模型是参数化模型，哪些模型是非参数化模型？

2. 经典机器学习

2-1. 特征工程

2-1-1. 你是怎样理解“特征”？
2-1-2. 给定场景和问题，你如何设计特征？（特征工程方法论）
2-1-3. 开发特征时候做如何做数据探索，怎样选择有用的特征？
2-1-4. 你是如何做数据清洗的？举例说明
2-1-5. 如何发数据中的异常值，你是如何处理？
2-1-6. 缺失值如何处理？
2-1-7. 对于数值类型数据，你会怎样处理？为什么要做归一化？归一化有哪些方法？离散些方法，离散化和归一化有哪些优缺点？
2-1-8. 标准化和归一化异同？
2-1-9. 你是如何处理CTR类特征？
2-1-10. 讲解贝叶斯平滑原理？以及如何训练得到平滑参数。
2-1-11. 类别型数据你是如何处理的？比如游戏品类，地域，设备
2-1-12. 序号编码、One-hot编码、二进制编码都是什么？适合怎样的类别型数据？
2-1-13. 时间类型数据你的处理方法是什么？原因？
2-1-14. 你怎样理解组合特征？举个例子，并说明它和单特征有啥区别
2-1-15. 如何处理高维组合特征？比如用户ID和内容D?
2-1-16. 如何理解笛卡尔积、外积、内积？
2-1-17. 文本数据你会如何处理？
2-1-18. 文本特征表示有哪些模型？他们的优缺点都是仕么？
2-1-19. 进解TFF原理，它有什么优点和缺点？针对它的缺点，你有什么优化思路？
2-1-20. N-gram算法是什么？有什么优缺点？
2-1-21. 讲解一下word2Vec工作原理？损失函数是什么？
2-1-22. 讲解一下LDA模型原理和训练过程？
2-1-23. Word2Vec和LDA两个模型有什么区别和联系？
2-1-24. Skip-gram和cbow有何异同？
2-1-25. 图像数据如何处理？有哪些常用的图像特征提取方法
2-1-26. 你是怎样做特征选择的？卡方检验、信息值(V)、VOE都是如何计算？
2-1-27. 计算特征之间的相关性方法有哪些？有什么优缺点

2-2. KNN

2-2-1. Knn建模流程是怎样的？
2-2-2. Knn优缺点是什么？
2-2-3. Knn适合什么样的场景和数据类型？
2-2-4. 常用的距离衡量公式都有哪些？具体说明它们的计算流程，以及使用场景？
2-2-5. 超参数K值过大或者过小对结果有什么影响，你是如何选择K值？
2-2-6. 介绍一下Kd树？如何建树，以及如何搜索最近节点？

2-3. SVM

2-3-1. 简单讲解SVM模型原理？
2-3-2. SVM为什么会对缺失值敏感？实际应用时候你是如何处理？
2-3-3. SVM为什么可以分类非线性问题？
2-3-4. 常用的核函数有哪些？你是如何选择不同的核函数的？
2-3-5. RBF核函数一定线性可分么？为什么
2-3-6. SVM属于线性模型还是非线性模型？为什么？
2-3-7. 训练误差为0的SVM分类器一定存在吗？说明原因？
2-3-8. 当用支持向量机进行分类时，支持向量越多越好还是越少越好？
2-3-9. 多类分类问题

2-4. 朴素贝叶斯

2-4-1. 讲解贝叶斯定理？
2-4-2. 什么是条件概率、边缘概率、联合概率？
2-4-3. 后验概率最大化的含义是什么？
2-4-4. 朴素贝叶斯模型如何学习的？训练过程是怎样？
2-4-5. 你如何理解生成模型和判别模型？
2-4-6. 朴素贝吐斯模型“朴素”体现在哪里？存在什么问题？有哪些优化方向？
2-4-7. 什么是贝吐斯网络？它能解决什么问题？
2-4-8. 为什么说朴素贝叶斯也是线性模型而不是非线性模型呢？
2-4-9 如何解决用极大似然法可能出现所要估计的概率为0的情况？

2-5. 线性回归

2-5-1. 线性回归的基本思想是？
2-5-2. 什么是“广义线性模型”？
2-5-3. 线性回归常用的损失函数有哪些？优化算法有哪些？
2-5-4. 线性回归适用什么类型的问题？有哪些优缺点？
2-5-5. 请用最小二乘法推倒参数更新公式？

2-6. 逻辑回归

2-6-1. 逻辑回归相比于线性回归有仕么异同？
2-6-2. 逻辑回归和广义线性模型有何关系？
2-6-3. 逻辑回归如何处理多标签分类？
2-6-4. 为什么逻辑回归需要进行归一化或者取对数？
2-6-5. 为什么逻辑回归把特征离散化之后效果会提升？
2-6-6. 类别不平衡问题你是如何处理的？什么是过采样，什么是欠采样？举例
2-6-7. 讲解L1和L2正则，它们都有什么作用，解释为什么L1比L2更容易产生稀疏解；对于存在线性相关的一组特征，L1正则如何选择
特征？
2-6-8. 使用交叉熵作为损失函数，梯度下降作为优化方法，推倒参数更新公式
2-6-9. 代码写出训练函数

2-7. FM模型

2-7-1. FM模型与逻辑回归相比有什么优缺点？
2-7-2. 为什么FM模型计算复杂度时O(kn)?
2-7-3. 介绍FFM场感知分解机器(Field-aware Factorization Machine),说说与FM异同？
2-7-4. 使用FM进行模型训练时候，有哪些核心参数对模型效果影响大？
2-7-5. 如何从神经网络的视角看待FM模型？

2-8. 决策树

2-8-1. 讲解完成的决策树的建树过程
2-8-2. 你是如何理解熵？从数学原理上解释熵公式可以作为信息不确定性的度量？
2-8-3. 联合熵、条件熵、KL散度、信息增益、信息增益比gi系数都是什么？如何计算？
2-8-4. 常用的决策树有哪些？ID3、C4.5、CART有啥异同？
2-8-5. 决策树如何防止过拟合？前剪枝和后剪枝过程是怎样的？剪枝条件都是什么？

2-9. 随机森林(RF)

2-9-1. 介绍RF原理和思想
2-9-2. RF是如何处理缺失值？
2-9-3. RF如何衡量特征重要度？
2-9-4. RF“随机”主要体现在哪里？
2-9-5. RF有哪些优点和局限性？
2-9-6. 为什么多个弱分类器组合效果会比单个要好？如何组合弱分类器可以获得更好的结果？原因是什么？
2-9-7. Bagging的思想是什么？它是降低偏差还是方差，为什么？
2-9-8. 可否将RF的基分类模型由决策树改成线性模型或者knn？为什么？

2-10. GBDT

2-10-1. 梯度提升和梯度下降有什么区别和联系？
2-10-2. 你是如何理解Boosting和Bagging?他们有什么异同？
2-10-3. 讲解GBDT的训练过程？
2-10-4. 你觉得GBDT训练过程中哪些环节可以平行提升训练效率？
2-10-5. GBDT的优点和局限性有哪些？
2-10-6. GBDT是否对异常值敏感，为什么？
2-10-7. 如何防止GBDT过拟合？
2-10-8. 在训练过程中哪些参数对模型效果影响比较大？这些参数造成影响是什么？

2-11. k-means

2-11-1. 简述kmeans建模过程？
2-11-2. Kmeans损失函数是如何定义？
2-11-3. 你是如何选择初始类族的中心点？
2-11-4. 如何提升kmeansi效率？
2-11-5. 常用的距离衡量方法有哪些？他们都适用什么类型问题？
2-11-6. Kmeans对异常值是否敏感？为仕么？
2-11-7. 如何评估聚类效果？
2-11-8. 超参数类的个数k如何选取？
2-11-9. Kmeans有哪些优缺点？是否有了解过改进的模型，举例说明？
2-11-10. 试试证明kmeans算法的收敛性
2-11-11. 除了kmeans聚类算法之外，你还了解哪些聚类算法？简要说明原理
2-11-12. kmeans初始化为什么要从数据中随机挑k个，可以生成k个随机点吗？

2.12. PCA降维

2-12-1. 为什么要对数据进行隆维？它能解决什么问题？
2-12-2. 你是如何理解维度灾难？
2-12-3. PCA主成分分析思想是什么？
2-12-4. 如何定义主成分？
2-12-5. 如何设计目标函数使得降维达到提取主成分的目的？
2-12-6. PCA有哪些局限性？如何优化
2-12-7. 线性判别分析和主成分分析在原理上有何异同？在目标函数上有何区别和联系？

3. 深度学习

3-1. DNN

3-1-1. 描述一下神经网络？推倒反向传播公式？
3-1-2. 讲解一下dropout原理？
3-1-3. 梯度消失和梯度膨胀的原因是什么？有什么方法可以缓解？
3-1-4. 什么时候该用浅层神经网络，什么时候该选择深层网络
3-1-5. Sigmoid、Relu Tanh激活函数都有哪些优缺点？
3-1-6. 写出常用激活函数的导数
3-1-7. 训练模型的时候，是否可以把网络参数全部初始化为0？为什么
3-1-8. Batchsize大小会如何影响收敛速度？

3-2. CNN

3-2-1. 简述CNN的工作原理？
3-2-2. 卷积核是什么？选择大卷积核和小卷积核有什么影响？
3-2-3. 你在实际应用中如何设计卷积核？
3-2-4. 为什么CNN具有平移不变性？
3-2-5. Pooling?操作是什么？有几种？作用是什么？
3-2-6. 为什么CNN需要pooling操作？
3-2-7. 什么是batchnormalization?它的原理是什么？在CNN中如何使用？
3-2-8. 卷积操作的本质特性包括稀疏交互和参数共享，具体解释这两种特性以其作用？
3-2-9. 你是如何理解fine-tune?有什么技巧

3-3. RNN

3-3-1. 简述RNN模型原理，说说RNN适合解决什么类型问题？为什么
3-3-2. RNN和DNN有何异同？
3-3-3. RNN为什么有记忆功能？
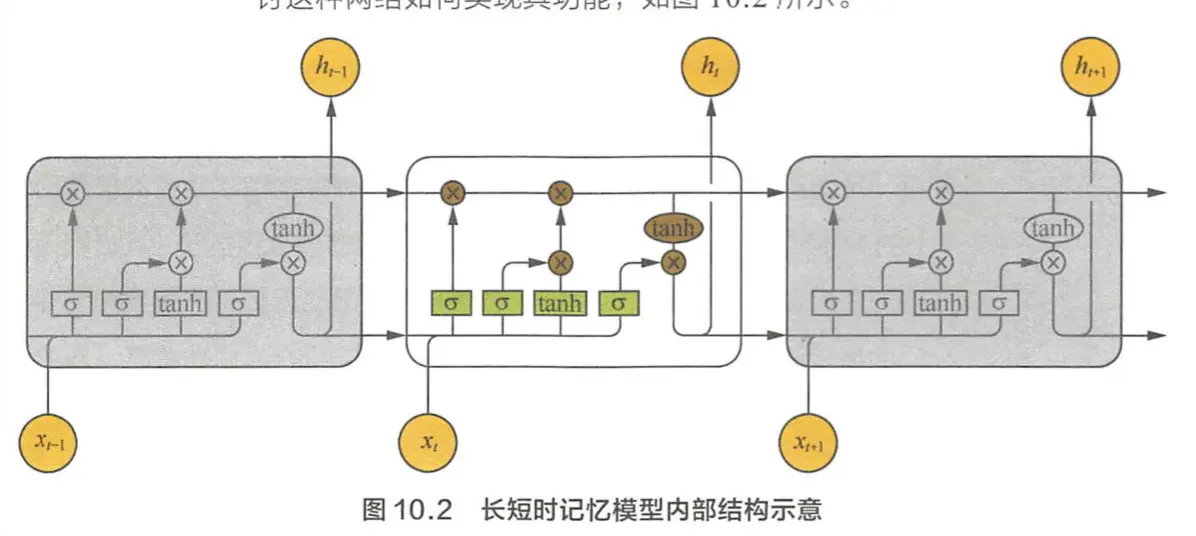
3-3-4. 长短期记忆网络LSTM是如何实现长短期记忆功能的？
3-3-5. 长短期记忆网络LSTM各模块都使用什么激活函数，可以使用其他激活函数么？
3-3-6. GRU和LSTM有何异同
3-3-7. 什么是Seg2Seg模型？该模型能解决什么类型问题？
3-3-8. 注意力机制是什么？Seg2Seg模型引入注意力机制主要解决什么问题？
3-3-9. RNN的长期依赖（Long-Term Dependencies）问题是什么？怎么解决
3-3-10. RNN为什么会产生梯度消失或者梯度爆炸
3-3-11. RNN如何解决梯度爆炸问题
3-3-12. RNN如何解决梯度消失问题
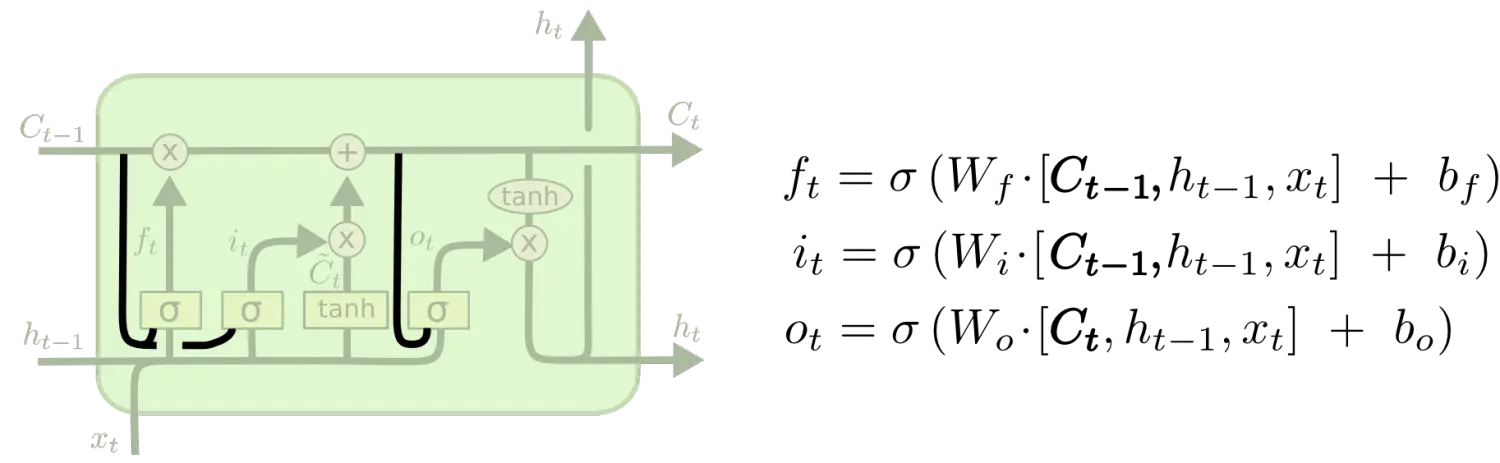
3-3-13. LSTM的结构，每个门的作用，计算公式
3-3-14. LSTM变种有哪些
3-3-15. LSTM为什么可以解决梯度消失

1. 机器学习

1-1. 解决机器学习问题的一般流程

1. 理解问题：明确问题的定义、目标和类型（回归、分类等），了解数据集的特征和限制条件。
2. 数据准备：收集、清洗和探索数据，包括处理缺失值、异常值和重复值，进行特征选择和特征工程。
3. 模型选择：根据问题类型和数据特征选择适当的机器学习算法模型，如线性回归、决策树、支持向量机等。
4. 模型训练：使用训练数据对选定的模型进行训练，通过优化算法最小化损失函数，调整模型参数使其与真实值尽可能接近。
5. 模型评估：使用评估指标对训练后的模型进行性能评估，例如准确度、精确度、召回率等。
6. 模型优化：根据评估结果进行模型优化，如调整超参数、尝试不同的特征工程方法或算法模型。
7. 模型部署：将优化后的模型应用于新的数据集，并进行实时预测或决策。

1-2. 损失函数

损失函数是衡量模型预测结果与真实值之间差异的函数。合理的损失函数应该具备以下特点：可微性（使得优化算法能够使用梯度信息进行参数更新）、非负性（损失不能为负值）和敏感性（能够准确度量预测误差）。

1-3. 分类回归常用损失函数

1. 0-1损失函数：

$$
L(f(x),y) =
\begin{cases}
1,
&
y \neq f(x) \
0,
&
y = f(x)
\end{cases}
$$

2. 绝对损失函数：异常点多的情况下鲁棒性好；但不方便求导

$$
L(f(x), y) = |f(x)-y|
$$

3. 平方损失函数：求导方便，能够用梯度下降法优化；对异常值敏感
   $$
   L(f(x),y) = (f(x)-y)^2
   $$

4. 对数损失函数/对数似然损失函数：
   $$
   L(P(Y|X),Y) = -{\rm log} P(Y|X)
   $$

5. Huber 损失函数：结合了绝对损失函数和平方损失函数的优点；缺点是需要调整超参数 $\delta$
   $$
   L_{Huber}(f, y) =
   \begin{cases}
   (f-y)^2
   &
   |f-y| \leq \delta
   \
   2 \delta |f-y| - \delta^2
   &
   |f-y| > \delta
   \end{cases}
   $$

6. Log-Cosh 损失函数：具有Huber的所有优点，同时二阶处处可微（牛顿法要求二阶可微）
   $$
   L(f,y) = \log \cosh(f-y)
   $$

• 常用的回归模型损失函数包括均方误差（Mean Squared Error，MSE）和平均绝对误差（Mean Absolute Error，MAE），其优缺点如下：
  • MSE：对异常值敏感，但在拟合平滑曲线时效果较好。
  • MAE：对异常值不敏感，但在存在离群点时可能会产生较大误差。
• 常用的分类模型损失函数包括交叉熵损失（Cross Entropy Loss）和支持向量机（SVM）损失，其优缺点如下：
  • 交叉熵损失：适用于二分类和多分类任务，能够更好地刻画类别之间的差异。
  • SVM损失：适用于二分类任务，对异常值不敏感，能够产生较大的间隔。

1-4. 结构误差与经验误差

• 结构误差指模型在整个数据分布上的误差，而经验误差指模型在训练集上的误差。判断模型是否达到最优通常是通过观察经验误差和结构误差之间的差距来评估，当二者差距较小且模型能够在新数据上良好泛化时，可认为模型已经达到最优。

1-5. 泛化能力

• 模型的”泛化”能力是指模型对未见过的数据的适应能力。要提升模型的泛化能力，可以采取以下策略：

  • 增加数据量：通过增加训练数据数量，使模型能够学习更多样的情况，从而提高泛化能力。

  • 特征选择和特征工程：选择与问题相关且具有代表性的特征，并进行适当的特征处理和变换，以提高模型的泛化能力。

  • 模型正则化：通过添加正则化项（如L1正则化、L2正则化）限制模型的复杂度，避免过拟合，提高泛化能力。

  • 验证集和交叉验证：使用验证集和交叉验证技术来评估模型在未见样本上的性能，帮助选择合适的模型和调整超参数，以提高泛化能力。

1-6. 混淆矩阵

小萌讲的嘎嘎好！！！

混淆矩阵是一种用于可视化分类模型性能的表格。它将模型的预测结果与真实标签进行对比，并将其分类为四个不同的类别：真正例（True Positive，TP）、真反例（True Negative，TN）、假正例（False Positive，FP）和假反例（False Negative，FN）。混淆矩阵的形式如下：

混淆矩阵	预测结果	预测结果
真实情况	反例	正例
反例	TN（真反例）	FP（假正例）
正例	FN（假反例）	TP（真正例）

• TN：True Negative，被判定为负样本，事实上也是负样本

• FP：False Positive，被判定为正样本，但事实上是负样本

• FN：False Negative，被判定为负样本，但事实上是正样本

• TP：True Positive，被判定为正样本，事实上也是正样本

混淆矩阵可以用于计算各种评估指标，如准确度、精准度、召回率等。

1-7. 指标

• 选择合适的模型评估指标取决于具体的问题和任务。以下是一些常见的模型评估指标：

  • AUC（Area Under the Curve）：用于二分类问题，表示ROC曲线下的面积，范围在0到1之间。AUC越接近1，表示模型性能越好。

  • 精准度（Precision）：在预测为正例的样本中，真实为正例的比例。

  • 召回率（Recall）：在所有真实为正例的样本中，被正确预测为正例的比例。

  • F1值：精准度和召回率的调和平均值，综合考虑了两者。F1值越高，表示模型的性能越好。

• 这些评估指标的计算公式如下：

  • AUC：通过绘制ROC曲线并计算曲线下的面积来得到。

  • 精准度：真正例数除以真正例数加假正例数。

  • 召回率：真正例数除以真正例数加假反例数。

  • F1值：2 * ((精准度 * 召回率) / (精准度 + 召回率))。

• 这些指标各有优缺点，选择适当的指标要根据具体问题的需求。比如，对于不平衡数据集，AUC和F1值通常更适合评估模型性能，因为它们能够综合考虑正负样本的预测结果。

${\color\red 分类任务指标}$

Accuracy（准确率）：分类正确的样本占总样本个数的比例
$$
Accuracy = \frac{n_{correct}}{n_{total}}
$$

• 缺点：不同类别的样本比例非常不均衡时，占比大的类别往往成为影响准确率的最主要因素。比如，当负样本占99%时，分类器把所有样本都预测为负样本也可以获得99%的准确率。
• 解决：可以使用每个类别下的样本准确率的算术平均（平均准确率）作为模型评估的指标。

Precision（精确率）：分类正确的正样本个数占分类器判定为正样本的样本个数的比例
$$
Precision = \frac{TP}{TP+FP}
$$
Recall（召回率）：分类正确的正样本数占真正的正样本个数的比例
$$
Recall = \frac{TP}{TP+FN}
$$
F1-score：precision和recall的调和平均值；当精确率和召回率都高时，F1值也会高
$$
{\rm F1} = \frac{2 \times precision \times recall}{precision + recall}
$$

在排序问题中，通常没有一个确定的阈值把得到的结果直接判定为正样本或负样本，而是采用Top N返回结果的Precision和Recall值来衡量排序模型的性能。即认为模型返回的Top N结果就是模型判定的正样本，计算前N个位置的Precision@N和Recall@N。为了综合评估一个排序模型的好坏，不仅要看模型在不同Top N下的Precision@N和Recall@N，而且最好画出模型的P-R曲线。P-R曲线的横轴是Recall，纵轴是Precision。

ROC：横坐标为假阳性率（False Positive Rate，FPR）；纵坐标为真阳性率（True Positive Rate，TPR）
$$
FPR = \frac{FP}{N} \
TPR = \frac{TP}{P}
$$
其中P是真实的正样本的数量，N是真实的负样本的数量，TP是P个正样本中被分类器预测为正样本的个数，FP是N个负样本中被预测为正样本的个数。

【如何绘制ROC曲线】通过不断移动分类器的“截断点”来生成曲线上的一组关键点。在二分类问题中，模型输出一般是预测样本为正例的概率，在输出最终的正例负例之前，我们需要制定一个阈值。大于该阈值的样本判定为正例，小于该阈值的样本判定为负例。通过动态调整截断点，绘制每个截断点对应位置，再连接所有点得到最终的ROC曲线。

AUC：ROC曲线下的面积大小。计算AUC值只要沿着ROC横轴做积分就可以。AUC取值一般在0.5~1之间。AUC越大，分类性能越好。AUC表示预测的正例排在负例前面的概率。

指标想表达的含义，简单来说其实就是随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率

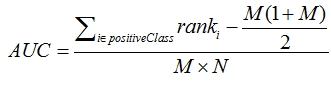
AUC为0.5表明对正例和负例没有区分能力，对于不论真实类别是1还是0，分类器预测为1的概率是相等的。

我们希望分类器达到的效果：对于真实类别为1的样本，分类器预测为1的概率（TPR）要大于真实类别为0而预测类别为1的概率（FPR），即y>x

AUC的计算方法同时考虑了分类器对于正例和负例的分类能力，在样本不平衡的情况下，依然能够对分类器作出合理的评价。

思路：1.首先对预测值进行排序，排序的方式用了python自带的函数sorted，详见注释。

　　　2.对所有样本按照预测值从小到大标记rank，rank其实就是index+1，index是排序后的sorted_pred数组中的索引

　　　3.将所有正样本的rank相加，遇到预测值相等的情况，不管样本的正负性，对rank要取平均值再相加

​ 4.将rank相加的和减去正样本排在正样本之后的情况，再除以总的组合数，得到auc

${\color\red 回归任务指标}$

RMSE：计算预测值和实际值的平均误差
$$
{\rm RMSE} = \sqrt{\frac{\sum_{i=1}^n (y_i-\hat{y}_i)^2}{n}}
$$

1-8. ROC

​ ROC曲线（Receiver Operating Characteristic Curve）是一种用于可视化二分类模型性能的曲线。ROC曲线的横轴是假正例率（False Positive Rate，FPR），纵轴是真正例率（True Positive Rate，TPR）。ROC曲线通过改变分类模型的阈值来绘制，每个阈值对应一个点，连接这些点形成曲线。

​ 相比而言，P-R曲线（Precision-Recall Curve）将精准度和召回率作为横纵轴，通过改变分类模型的阈值来绘制。ROC曲线关注的是真正例率和假正例率的变化，而P-R曲线关注的是精准度和召回率的变化。

​ ROC曲线和P-R曲线都可以用于评估模型的性能，选择哪种曲线取决于具体问题的需求。一般来说，当正负样本分布不平衡时，P-R曲线更能反映模型的性能。

1-9. 过拟合与欠拟合

​ 当模型在训练集上表现良好但在验证集（或测试集）上表现较差时，通常表示模型存在过拟合（Overfitting）的问题。过拟合指模型过度拟合了训练数据中的噪声和细节，导致在新数据上的泛化能力较差。过拟合的主要原因是模型过于复杂，参数过多，从而过度适应了训练数据。

• 过拟合的特征包括：

  • 训练集上的损失函数较低，但验证集上的损失函数较高。

  • 模型在训练集上的预测表现良好，但在新数据上的预测效果较差。

  • 模型的参数值较大，波动较大，对训练数据中的噪声极度敏感。

• 解决过拟合问题的常见方法包括：

  • 数据增强（Data Augmentation）：通过对训练数据进行随机变换、扩充数据集规模，以增加数据的多样性，从而减少模型对训练数据的过度依赖。

  • 正则化（Regularization）：通过在损失函数中添加正则化项，如L1正则化或L2正则化，限制模型参数的大小，避免过拟合。

  • 早停（Early Stopping）：在训练过程中监控模型在验证集上的性能，当性能不再提升时停止训练，防止模型过度拟合训练数据。

  • 简化模型结构：减少模型的复杂度，如减少参数的数量、降低模型的层数或宽度，以防止模型过拟合。

  • Dropout：在训练过程中随机丢弃一部分神经元，使得模型不能过度依赖某些特征，从而减少过拟合。

​ 相反，欠拟合（Underfitting）指模型无法捕捉到数据中的重要模式和关系，无法充分拟合训练数据。欠拟合的主要原因是模型过于简单或训练数据量不足。

• 欠拟合的特征包括：

  • 模型在训练集和验证集上的性能都较差。

  • 模型在训练集上的损失函数较高，无法很好地拟合训练数据。

• 解决欠拟合问题的常见方法包括：

  • 增加模型复杂度：增加模型的层数、宽度或参数数量，使其能够更好地拟合数据。

  • 特征工程：增加更多的特征或改进现有特征，以提高模型对数据的表达能力。

  • 收集更多数据：增加训练数据量，使模型有更多的样本进行学习。训练轮次更多。

  • 调整超参数：调整模型的超参数，如学习率、正则化参数等，以获得更好的模型性能。

​ 在实际应用中，过拟合和欠拟合是常见的挑战之一。为了找到合适的模型复杂度，通常需要进行反复的实验和调优，同时要注意避免过拟合和欠拟合的极端情况，以获得更好的模型泛化能力。

1-10. 模型选择技巧

1. 应用场景和任务要求：了解所需解决的具体问题，并确定模型需要具备的能力，例如分类、回归、生成等。
2. 数据情况：了解数据的属性、规模和特点，例如数据的维度、样本数量、噪声水平等。这有助于判断哪种类型的模型更适合处理数据。
3. 模型复杂度：根据问题的复杂程度和数据的复杂性，选择适当的模型复杂度。过于简单的模型可能无法捕捉到数据中的复杂关系，而过于复杂的模型可能会导致过拟合。
4. 可用资源：考虑可用的计算资源和时间限制。一些复杂的模型可能需要更多的计算资源和训练时间。
5. 先前的研究和实践经验：查阅领域内的文献和先前的实践经验，了解在类似问题上哪些模型取得了良好的性能。
6. 集成方法：考虑使用集成方法，如随机森林、梯度提升树等，将多个模型的预测结果进行组合，以提高整体性能。

1-11. 超参数选择

• 主要方法

  • 手动调整：通过经验和直觉进行手动调整。这需要领域知识和对模型的理解，但是耗时且不一定能找到最佳参数。

  • 网格搜索：定义一个超参数的候选集合，然后遍历所有可能的超参数组合，通过交叉验证或验证集性能选择最佳参数。实际应用中先用较大搜索范围和较大步长，寻找全局最优值可能位置；然后逐步缩小搜索范围和搜索步长，寻找更精确位置。优点：简单，如果采用较大的搜索范围和较小步长，有很大概率找到全局最优值。缺点：耗时，目标函数非凸时，可能错过全局最优解。

  • 随机搜索：不再测试上界和下界之间的所有值，而是在搜索范围中随机选取样本点。如果样本点集足够大，通过随机搜索也能大概率找到全局最优解或其近似。在超参数空间中随机选择一组参数进行评估。这种方法相对于网格搜索计算成本较低，可以在较短时间内对大范围的参数空间进行搜索。优点：更快，缺点：可能错过全局最优解。

  • 贝叶斯优化：使用贝叶斯方法建立超参数与模型性能之间的映射关系，并根据之前的观察结果选择下一个要评估的超参数组合。这种方法通常能够在相对较少的迭代中找到性能较好的超参数。对目标函数形状进行学习，找到使目标函数向全局最优值提升的参数。优点：不同于前两种方法测试一个新点时会忽略前一个点的信息；贝叶斯优化算法充分利用之前的信息。缺点：容易陷入局部最优值。

• 每种方法都有其优点和局限性，选择哪种方法取决于问题的复杂性、可用资源和时间限制。

1-12. 误差分析

• 误差分析是一种评估模型性能和理解模型预测错误的方法。它涉及对模型在测试数据上的预测结果进行分析，以确定模型在哪些情况下表现良好或较差。误差分析的步骤通常包括：

  1. 收集模型的预测结果和真实标签。
  2. 对预测错误的样本进行分类和统计，了解错误的类型和频率。
  3. 分析错误的原因，可能涉及数据质量问题、标签错误、模型假设不匹配等。
  4. 根据分析结果，采取措施改进模型，例如增加训练数据、调整模型复杂度、改进特征工程等。

• 误差诊断：通过训练误差和测试误差来分析模型是否存在高方差、高偏差。

  • 如果训练误差较高：说明模型的偏差较大，模型出现了欠拟合。
  • 如果训练误差较低，而测试误差较高：说明模型的方差较大，出现了过拟合。
  • 如果训练误差较低，测试误差也较低：说明模型的方差和偏差都适中，是一个比较理想的模型。
  • 如果训练误差较高，且测试误差更高：说明模型的方差和偏差都较大。

上述分析的前提是：训练集、测试集的数据来自于同一个分布，且最优误差较小。否则讨论更复杂。

1-13. 偏差和方差

• 偏差（Bias）是指模型在训练过程中对问题的错误假设或错误的模型选择而导致的误差。高偏差意味着模型对数据的拟合能力较差，无法捕捉到数据中的复杂关系。在训练集和测试集上都表现较差。高偏差对应于模型的欠拟合。
• 方差（Variance）是指模型在训练过程中对训练数据的敏感性。高方差意味着模型对训练数据过拟合，对噪声和随机性过于敏感，导致在测试集上表现较差。高方差对应于模型的过拟合。

1-14. 高偏差和高方差优化策略

参考1-9

• 高偏差的优化策略：
  • 增加模型复杂度：增加模型的容量，例如增加隐藏层或增加模型的参数数量，以使其能够更好地拟合训练数据。
  • 改进特征工程：引入更多的特征或更复杂的特征表示，以提供更多的信息给模型。
  • 增加训练数据：增加训练数据的数量可以帮助模型更好地学习数据的分布和模式。
• 高方差的优化策略：
  • 减少模型复杂度：降低模型的容量，例如减少隐藏层或减少模型的参数数量，以减少过拟合的风险。
  • 正则化：通过在损失函数中引入正则化项，如L1正则化或L2正则化，来惩罚模型的复杂性，防止过拟合。
  • 数据增强：通过对训练数据进行扩充、旋转、裁剪等操作，增加数据的多样性，提高模型的泛化能力。

1-15. 奥卡姆剃刀定律

• 奥卡姆剃刀定律是一种科学原理，也称为奥卡姆的剃刀。它的核心思想是在解释某个现象或问题时，应该选择最简洁且能够解释观察结果的假设或解释。换句话说，当有多个解释或模型能够解释观察到的现象时，应该选择最简单的解释或模型。对于机器学习模型优化的启发，奥卡姆剃刀定律提醒我们在选择模型复杂度、特征选择和解释模型结果时要保持简单性。过于复杂的模型可能会导致过拟合，而过于复杂的特征选择或解释可能会引入不必要的复杂性。
• 举例来说，当解释一个分类问题时，如果一个简单的线性模型能够达到与复杂的深度神经网络相当的性能，那么根据奥卡姆剃刀定律，选择线性模型可能是更好的选择，因为它更简单且更易解释。

1-16. 线性模型与非线性模型

线性与非线性

​ 非概率模型可以分为线性模型和非线性模型。如果函数 $y=f(x)$ 或 $z = g(x)$​ 是线性函数，则称模型是线性模型，否则成模型为非线性模型。线性模型是指模型的输出是输入特征的线性组合，即模型的预测结果可以表示为输入特征的加权和。线性模型的决策边界是一个线性函数。线性模型具有简单、可解释性强的特点，但对于复杂的非线性关系建模能力有限。非线性模型允许模型的输出与输入特征之间存在非线性的关系。这意味着模型可以更好地拟合复杂的数据模式和关系。非线性模型的决策边界可以是曲线、曲面或更复杂的形状。

• 线性模型：感知机、线性支持向量机、k近邻、k均值、潜在语义分析。
• 非线性模型：核函数支持向量机、AdaBoost，神经网络。

1-17. 生成式模型和判别式模型

​ 监督学习方法分为生成方法（generative approach）和判别方法（discriminative approach）。所学习到的模型分别称为生成模型和判别模型。监督学习的模型一般形式为决策函数：$Y = f(X)$ 或者条件概率分布 $P(Y|X)$。生成方法由数据学习联合概率分布 $P(X,Y)$，然后求出条件概率分布 $P(Y|X)$作为预测模型：
$$
P(Y|X) = \frac{P(X,Y)}{P(X)}
$$
​ 之所以成为生成方法，是因为模型表示了给定输入 $X$ 产生输出 $Y$的生成关系。典型的生成模型：朴素贝叶斯法、隐马尔可夫模型。判别方法由数据直接学习决策函数 $f(X)$ 或者条件概率分布 $P(X,Y)$作为预测的模型，关心的是对给定的输入 $X$，应该预测什么样的输出 $Y$。典型的判别模型：k近邻、感知机、决策树、逻辑斯蒂回归、最大熵模型、支持向量机、提升方法、条件随机场。

1-18. 概率模型和非概率模型

​ 概率模型与非概率模型的区别在于模型的内在结构。概率模型一定可以表示为联合概率分布的形式，其中的变量表示输入、输出、因变量甚至参数。而针对非概率模型则不一定存在这样的联合概率分布。

​ 统计学习的模型可以分为概率模型（probabilistic model）和非概率模型（non-probabilistic model）或者确定性模型（deterministic model）。在监督学习中，概率模型取条件概率分布形式 $p(y|x)$，非概率模型取函数形式 $y=f(x)$，其中$x$是输入，$y$是输出。在无监督学习中，概率模型取条件概率分布形式 $p(z|x)$或 $p(x|z)$，其中$x$是输入，$z$是输出。在监督学习中，概率模型是生成模型，非概率模型是判别模型。

• 概率模型：决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分布、高斯混合模型
• 非概率模型：感知机、支持向量机、k近邻、AdaBoost、k均值、潜在语义分析、神经网络

​ 逻辑斯蒂回归即可看做概率模型，又可看做非概率模型。

1-19. 参数化模型和非参数化模型

​ 统计学习模型又可以分为参数化模型（parametric model）和非参数化模型（non-parametric model）。参数化模型假设模型参数的维度固定，模型可以由有限维参数完全刻画；非参数模型假设模型参数的维度不固定或者说无穷大，随着训练数据量的增加而不断增大。

• 参数化模型：感知机、朴素贝叶斯、逻辑斯蒂回归、k均值、高斯混合模型

• 非参数化模型：决策树、支持向量机、AdaBoost、k近邻、潜在语义分析、概率潜在语义分析、潜在狄利克雷分配

2. 经典机器学习

2-1. 特征工程

2-1-1. 特征

​ 特征是指在数据中表示某种属性或特性的变量或属性。在机器学习和数据分析中，特征用于描述样本或数据点的不同方面，以便用于建模和分析。计算机通过特征去认识样本，样本在计算机眼中是特征向量。

2-1-2. 如何设计特征

在设计特征时，可以根据以下方法论进行：

• 领域知识：了解业务和问题的背景，从中提取与问题相关的特征。
• 特征衍生：通过对已有特征进行数学运算、组合或转换，生成新的特征。
• 特征选择：使用统计方法或机器学习算法选择最相关或最重要的特征。
• 特征缩放：对特征进行缩放，使其具有相似的尺度或范围，以防止某些特征对模型产生过大影响。

2-1-3. 特征选择

在开发特征时，可以采取以下方法进行数据探索和选择有用的特征：

• 可视化分析：使用图表、直方图和散点图等可视化工具，观察特征与目标之间的关系。
• 相关性分析：计算特征与目标之间的相关性系数，选择具有较高相关性的特征。
• 特征重要性：使用机器学习算法（如决策树）计算特征的重要性得分，选择得分较高的特征。
• 领域知识：依靠专业领域知识，选择对问题有意义的特征。

2-1-4. 数据清洗

数据清洗是指对数据进行预处理，以修复或删除数据中的错误、缺失、重复或不一致的部分。例如，数据清洗可以包括删除重复记录、处理缺失值、纠正错误数据等。

2-1-5. 如何发现异常值

• 可视化分析：绘制箱线图、直方图或散点图，查看是否存在与其他数据点明显不同的异常值。
• 统计方法：计算数据的均值、标准差和离群值阈值，将超出阈值范围的值视为异常值。
• 领域知识：依靠对数据和问题领域的理解，识别可能存在的异常情况。

异常值的处理方式可以是删除异常值、将其视为缺失值进行处理，或者使用插值等方法进行填充。

2-1-6. 缺失值处理方式

• 删除缺失值：如果缺失值的比例较小且对整体数据影响较小，可以直接删除缺失值所在的样本或特征。
• 删除缺失值：如果缺失值的比例较多.直接将该特征舍弃掉，否则可能反倒会带入较大的噪声，对结果造成不良影响。
• 缺失值较少,其余的特征缺失值都在10%以内，我们可以采取很多的方式来处理:
  1. 把NaN直接作为一个特征，假设用0表示； （离散特征取值k维扩充到k+1维）
  2. 用均值填充； （连续特征-均值，离散特征-特征取值的众数）
  3. 用随机森林等算法预测填充

2-1-7. 数值类型数据处理、归一化、离散化

归一化

为了消除数据特征之间的量纲影响，我们需要对特征进行归一化处理，使得不同指标之间具有可比性。以梯度下降过程为例，如果不做归一化，在学习速率相同的情况下，大量纲变量的更新速度会大于小量纲，需要较多迭代才能找到最优解。如果将其归一化到相同的数值区间后，更新速度变得更为一致，容易更快地通过梯度下降找到最优解。常用的归一化方法

（1）线性函数归一化（Min-Max Scaling）

对原始数据进行线性变化，使结果映射到[0，1]范围，实现对原始数据的等比缩放。
$$
X_{norm} = \frac{X-X_{min}}{X_{max}-X_{min}}
$$
适用于有固定取值范围的数据，如图像数据[0，255]；不适用于有异常值的数据，例如有异常大的数值，其他数据会被压缩到很小的数值。最小-最大归一化保留了原始数据的分布形状和相对关系。

（2）零均值归一化（Z-score Normalization）

将原始数据映射到均值为0、标准差为1的分布上。Z-score标准化可以使数据分布具有零均值和单位方差，适用于对数据分布形状没有假设要求的情况。假设原始特征的均值为 $\mu$，方差为 $\sigma$ ，那么归一化公式定义为
$$
z = \frac{x-\mu}{\sigma}
$$

• 哪些机器学习算法不需要做归一化处理？概率模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率（不直接用变量的值，用变量的分布），如决策树、RF。而像Adaboost、GBDT、XGBoost、SVM、LR、KNN、KMeans之类的最优化问题就需要归一化。

离散化

• 离散化是将连续型数值特征转换为离散型特征的方法。离散化的优点包括：

  • 可以处理某些算法对连续型数据不敏感的情况，如决策树等。

  • 可以减少异常值的影响，使得模型更稳定。

• 离散化的缺点包括：

  • 信息损失：离散化将连续的数据转换为有限的离散值，可能会导致信息损失。
  • 维度增加：离散化后的特征会增加维度，导致特征空间变得更大，可能会增加模型的复杂性和计算开销。

归一化保留了原始数据的分布形状和相对关系，不会引入额外的维度，因此在一般情况下更常用。然而，对于某些特定问题，离散化可能更适合，例如需要将连续特征映射到有限的桶（bins）中，以捕捉特征的分段效应。选择归一化还是离散化要根据具体问题和数据的特点来决定。

2-1-8. 标准化和归一化

• 标准化（Standardization）：也称为Z-score标准化，通过减去均值并除以标准差，将数据转换为均值为0，标准差为1的分布。标准化后的数据具有零均值和单位方差，适用于对数据分布的形状没有假设要求的情况。
• 归一化（Normalization）：将数据按比例缩放到一个特定的范围，通常是[0, 1]或[-1, 1]之间。归一化可以保留原始数据的相对关系，并将数据映射到指定的范围内。归一化常用于对特征的大小和幅度进行统一处理，并且对于那些对数据分布范围敏感的算法（如K近邻和神经网络）特别有用。

2-1-9. 处理CTR类特征

什么是CTR

在处理CTR（Click-Through Rate）类特征时，常见的做法是进行独热编码（One-Hot Encoding）或者特征哈希化（Feature Hashing）。

1. 独热编码：对于CTR类特征，可能存在多个离散的取值，如广告位、广告类型等。独热编码将每个特征的每个取值都转化为一个二进制的特征列，其中只有一个位置为1，其余位置为0。这种编码方式可以保留原始特征的信息，同时避免了特征之间的大小关系对模型产生影响。但是，独热编码会导致特征维度的增加，可能在高基数特征的情况下引起稀疏性问题。
2. 特征哈希化：特征哈希化是一种将特征映射到固定长度的特征向量的方法。通过将特征值通过哈希函数映射到一个固定大小的空间，将特征的维度缩减到一个较小的固定维度。这种方法可以有效地解决高基数特征带来的稀疏性问题，并减少内存消耗。但是，特征哈希化可能会引起哈希冲突，即不同的特征值可能被映射到相同的哈希桶中，可能会导致信息损失。

除了上述方法外，还可以考虑其他特征工程技术，如组合特征、离散化等，以根据具体情况提取CTR类特征的有效信息。此外，在使用CTR类特征时，常用的模型包括逻辑回归、GBDT（梯度提升决策树）和深度学习模型等。具体选择哪种方法和模型取决于数据集的规模、特征的性质以及任务的要求。

2-1-10. 贝叶斯平滑

贝叶斯平滑（Bayesian smoothing），也称为拉普拉斯平滑（Laplace smoothing）或加一平滑（Add-one smoothing），是一种用于解决概率估计中零概率问题的技术。它通过在每个计数上添加一个平滑参数（通常为1），来避免在估计中出现概率为零的情况。

贝叶斯平滑的核心原理是基于贝叶斯定理和最大似然估计。在最大似然估计中，我们根据观察到的频率来估计概率。然而，当某个事件没有在训练数据中出现时，最大似然估计会将其概率估计为零，这可能不符合实际情况。

贝叶斯平滑通过引入平滑参数，将每个计数加上一个常数（通常是1），并将分母加上相应的平滑参数乘以类别的数量。这样做的效果是，在计算概率时，每个类别的概率都会略微降低，而不会为任何类别给出概率为零的情况。

训练得到平滑参数的方法可以通过以下步骤进行：

1. 统计每个类别的计数：对于每个类别，统计在训练数据中该类别出现的次数。
2. 计算类别的总计数：将所有类别的计数相加，得到总的类别计数。
3. 计算平滑参数：平滑参数通常取为1，但也可以根据具体情况进行调整。
4. 计算平滑后的概率：对于每个类别，将其计数加上平滑参数，分母加上平滑参数乘以类别的总计数，然后计算平滑后的概率。

贝叶斯平滑的效果是在概率估计中引入了一定的平滑性，避免了零概率问题。然而，值得注意的是，贝叶斯平滑可能会引入一定的偏差，因为它在概率估计中引入了额外的信息。因此，在使用贝叶斯平滑时，需要权衡平滑的效果和可能引入的偏差。

2-1-11. 类别型数据处理

比如游戏品类，地域，设备

one-hot编码

2-1-12. 序号编码、0ne-hot编码、二进制编码

​ 序号编码（Label Encoding）是一种将类别型数据映射为整数标签的方法。每个类别值被赋予一个唯一的整数编码，从0开始递增。序号编码适用于类别之间存在一定顺序关系的情况，例如衣服尺寸（小、中、大）或教育程度（高中、本科、硕士、博士）等。

​ 独热编码（One-Hot Encoding）是一种将类别型数据转化为二进制特征向量的方法。对于每个类别特征，创建一个新的二进制特征列，其中只有一个位置为1，表示该样本属于该类别，其他位置为0。独热编码适用于类别之间无序且无大小关系的情况，例如颜色（红、绿、蓝）或地区（东部、西部、南部、北部）等。

​ 二进制编码（Binary Encoding）是一种将类别型数据转化为二进制特征的方法。对于每个类别特征，将其映射为一个由二进制表示的编码。二进制编码可以有效地减少特征维度，并且在一定程度上保留了类别之间的关联关系。它适用于类别数量较多且需要降低维度的情况。

• 总结起来

  • 序号编码适用于类别之间存在顺序关系的情况。

  • 独热编码适用于类别之间无序且无大小关系的情况。

  • 二进制编码适用于类别数量较多且需要降低维度的情况。

​ 需要根据具体问题和数据集的特点选择适当的编码方式。同时，还可以考虑其他编码方法，如特征嵌入（Feature Embedding）等，以更好地表示类别型数据。

2-1-13. 时间类型数据处理

1. 时间戳表示：将时间转换为时间戳的形式，即某个固定时间点以来的秒数或毫秒数。时间戳可以方便地进行计算和排序，适用于需要对时间进行数值化处理的场景。
2. 分解时间特征：将时间拆分为年、月、日、小时等单独的特征。这样可以捕捉到时间的周期性变化和趋势，例如在某个月份或小时段内的行为模式可能会有所不同。
3. 周期性编码：对于具有明显周期性的时间数据，例如星期几、季节等，可以使用周期性编码方法，如正弦余弦编码，将时间数据映射到一个周期内的连续变量。

选择适当的处理方法取决于具体的任务和需求。例如，如果需要对时间进行排序或计算时间差，时间戳表示是一个常见的选择。如果需要捕捉时间的周期性变化，可以使用分解时间特征或周期性编码。

2-1-14. 组合特征、单特征

​ 组合特征指的是通过将多个单独的特征进行组合，形成新的特征。组合特征可以通过特征交叉、特征组合等方式得到。举个例子，假设有两个特征：性别和年龄段。单特征是指单独使用性别或年龄段作为特征。而组合特征可以是将性别和年龄段进行组合，形成新的特征，例如”性别-年龄段”。这样的组合特征可以带来更多的信息，例如性别和年龄段的交互作用。

​ 组合特征与单特征的区别在于，单特征只包含单一的特征信息，而组合特征结合了多个特征，可以提供更加丰富和复杂的信息。组合特征可以帮助模型更好地捕捉特征之间的关联关系和非线性关系，从而提高模型的表达能力。

2-1-15. 高维组合特征

1. 特征哈希（Feature Hashing）：使用哈希函数将高维组合特征映射到固定长度的特征空间。特征哈希可以将高维特征降维到较低的维度，并且具有较好的计算效率。
2. 特征交叉：对于高维组合特征，可以通过特征交叉的方式将其拆分成多个低维特征。例如，对于用户D和内容D的组合特征，可以将其分别作为用户特征和内容特征，然后进行特征交叉得到新的特征。
3. 嵌入（Embedding）：对于高基数的组合特征，可以使用嵌入技术将其映射到低维的连续向量空间。嵌入可以捕捉到组合特征之间的语义关系和相似度，并且适用于各种机器学习算法。

选择合适的处理方法需要根据具体问题和数据集的特点进行评估。对于高维组合特征，需要考虑维度灾难的问题，并选择适当的方法来降低维度并保留有用的信息。

2-1-16. 笛卡尔积、外积、内积

​ 笛卡尔积（Cartesian Product）是指两个集合之间的所有可能的组合。对于两个集合A和B，它们的笛卡尔积是一个新的集合，其中每个元素都是由A和B中的元素组合而成的。举个例子，假设集合A = {1, 2}，集合B = {a, b}，它们的笛卡尔积为{(1, a), (1, b), (2, a), (2, b)}。可以看到，笛卡尔积包含了A和B中所有元素的组合。

​ 外积（Outer Product）是矩阵运算中的概念，表示两个向量的乘积。对于两个向量a = [a1, a2, …, an]和b = [b1, b2, …, bm]，它们的外积是一个n×m的矩阵，其中第(i, j)个元素是ai乘以bj。

​ 内积（Inner Product），也称为点积或数量积，是两个向量的乘积与它们之间的夹角的余弦值的乘积。对于两个向量a = [a1, a2, …, an]和b = [b1, b2, …, bn]，它们的内积是一个标量，计算公式为a*b = a1*b1 + a2*b2 + … + an*bn。

• 总结起来：

  • 笛卡尔积是两个集合之间的所有可能组合的集合。

  • 外积是两个向量的乘积，得到一个矩阵。

  • 内积是两个向量的乘积与它们之间夹角的余弦值的乘积，得到一个标量。

2-1-17. 文本数据处理

1. 文本清洗：去除文本中的特殊字符、标点符号、HTML标签等干扰项，将文本转换为统一的格式。
2. 分词：将文本拆分成单词或词语的序列。常见的分词方法包括基于规则的方法、基于统计的方法（如n-gram）、基于机器学习的方法（如条件随机场）等。
3. 去除停用词：停用词是指在文本中频繁出现但往往不携带太多信息的词语，例如”的”、”是”等。可以使用预定义的停用词表或基于文本频率进行停用词的过滤。
4. 词干化或词形归一化：将词语还原到其原始的词干或词形，以减少词语的变体带来的维度灾难。常见的方法有基于规则的词干化和基于词典的词形归一化。
5. 构建词汇表：将分词后的词语构建成一个词汇表，用于后续的特征表示。
6. 特征表示：将文本转换为数值化的特征向量。常见的表示方法包括词袋模型（Bag-of-Words）、TF-IDF、词嵌入（Word Embedding）等。
7. 特征选择：根据任务需求和模型性能，对特征进行选择和筛选，以减少维度和噪声，提高模型的效果。
8. 序列建模：对于具有序列性质的文本数据，如文本分类、情感分析等任务，可以使用循环神经网络（RNN）或者Transformer等模型进行序列建模。

2-1-18. 文本模型和优缺点

1. 词袋模型（Bag-of-Words）：将文本看作是词语的集合，忽略词语之间的顺序和语法结构，只关注词语的频率。优点是简单快速，缺点是无法捕捉词语的顺序信息和语义关系。
2. TF-IDF：TF-IDF（Term Frequency-Inverse Document Frequency）是一种基于词频和逆文档频率的表示方法。它可以衡量词语在文本中的重要性，并降低常见词语的权重。优点是能够突出关键词，缺点是忽略了词语的顺序和语义信息。
3. 词嵌入（Word Embedding）：词嵌入是将词语映射到一个低维的连续向量空间，使得具有相似语义的词语在向量空间中距离较近。常见的词嵌入模型有Word2Vec、GloVe和FastText等。优点是能够捕捉词语的语义信息，缺点是无法处理未登录词和上下文外的信息。
4. 文档嵌入（Document Embedding）：文档嵌入是将整个文档映射到一个低维的连续向量空间，表示整个文档的语义信息。常见的文档嵌入模型有Doc2Vec和BERT等。优点是能够捕捉文档的整体语义信息，缺点是计算复杂度较高。

不同的特征表示模型适用于不同的任务和数据情况。词袋模型和TF-IDF（续）适用于简单的文本分类和信息检索任务，而词嵌入和文档嵌入则适用于更复杂的语义理解和文本生成任务。

词袋模型（Bag of Words）：每篇文章看成一袋子词，并忽略每个词出现的顺序。每篇文章可以表示成一个长向量，向量中的每一位代表一个单词，该维对应的权重则反映这个词在原文章中的重要程度，常用TF-IDF来计算权重。

缺点：无法识别出两个不同的词或者词组具有相同的主题。

TF-IDF

N-gram模型：将连续出现的n个词（n<=N）组成的词组也作为一个单独的特征放到向量表示中。

缺点：无法识别出两个不同的词或者词组具有相同的主题。

主题模型（Topic Model）：是一种特殊的概率图模型

词嵌入模型（Word Embedding）：将词向量化；核心思想是将每个词映射到低维空间（K=50~300维）上的一个稠密向量。K维空间的每一维也可以看作一个隐含的主题

2-1-19. TFF

TFF（Term Frequency-Filter Frequency）是一种特征选择方法，用于选择对于分类任务有用的特征。其原理是根据特征的词频和文档频率进行评估，词频高且文档频率低的特征被认为对于分类任务更有区分度。TFF的优点是简单高效，并且能够过滤掉一些噪声特征。然而，TFF也存在一些缺点，比如无法处理语义相关的特征，只考虑了词频和文档频率，忽略了特征间的关联性。针对TFF的缺点，可以考虑以下优化思路：

1. 结合语义信息：可以使用词嵌入等方法来捕捉特征的语义信息，从而更好地评估特征的区分度。
2. 考虑特征关联性：可以引入特征之间的关联性，比如共现信息或者相关性，来更准确地评估特征的重要性。
3. 动态特征选择：可以考虑在模型训练过程中动态地选择特征，根据模型的性能和特征的贡献度进行调整，以适应不同的任务和数据。

2-1-20. N-gram

​ N-gram算法是一种基于统计的文本特征表示方法，用于捕捉词语之间的顺序信息。N-gram将文本分割为连续的N个词语组成的序列，每个N-gram作为一个特征。例如，对于句子”我爱自然语言处理”，2-gram表示为[“我爱”, “爱自然”, “自然语言”, “语言处理”]。

• N-gram算法的优点包括：

  • 捕捉上下文信息：N-gram能够捕捉词语之间的顺序信息，可以反映上下文的语义。
  • 简单快速：N-gram算法的计算简单快速，适用于大规模文本数据。

• N-gram算法的缺点包括：

  • 维度爆炸：当N值较大时，N-gram会导致特征维度的爆炸，增加了模型的复杂度和计算负担。
  • 数据稀疏性：对于稀疏的数据，N-gram可能会导致很多未登录词或低频词的特征，影响模型的性能。
  • 无法处理长文本：对于长文本，N-gram可能无法捕捉到较远距离的词语关系，限制了其应用范围。

2-1-21. word2Vec

​ word2Vec是一种用于学习词嵌入的模型，其工作原理基于词语的分布假设。word2Vec通过训练神经网络，将词语映射到一个低维的连续向量空间，使得具有相似语义的词语在向量空间中距离较近。word2Vec模型有两个主要的训练算法：CBOW（Continuous Bag-of-Words）和Skip-gram。CBOW模型通过上下文词语的词向量来预测目标词语，而Skip-gram模型则通过目标词语来预测上下文词语。

​ word2Vec模型的损失函数是基于最大似然估计的。对于CBOW模型，损失函数是最大化目标词语的条件概率，即给定上下文词语，预测目标词语的概率。而对于Skip-gram模型，损失函数是最大化上下文词语的条件概率，即给定目标词语，预测上下文词语的概率。具体来说，CBOW模型的损失函数可以表示为：$L = sum(log P(w_t | w_c))$，其中，$w_t$表示目标词语，$w_c$表示上下文词语，$P(w_t | w_c)$表示给定上下文词语预测目标词语的概率。Skip-gram模型的损失函数可以表示为：$L = sum(sum(log P(w_c | w_t)))$，其中，$w_t$表示目标词语，$w_c$表示上下文词语，$P(w_c | w_t)$表示给定目标词语预测上下文词语的概率。

​ 通过最大化损失函数，word2Vec模型可以学习到词语的向量表示，使得具有相似语义的词语在向量空间中距离接近。这些学习到的词向量可以应用于各种自然语言处理任务，如词语相似度计算、文本分类、情感分析等。需要注意的是，word2Vec模型是一种无监督学习方法，它是通过大规模的未标注文本进行训练，从中学习到词语的语义表示。

2-1-22. LDA

​ LDA（Latent Dirichlet Allocation）模型是一种用于主题建模的概率生成模型。它假设文档是由多个主题组成的，并且每个主题又由多个单词组成。LDA模型的目标是通过观察到的文档集合来推断出每个文档的主题分布以及每个主题的单词分布。LDA模型的训练过程可以概括为以下几个步骤：

1. 初始化：为每个文档中的每个单词随机指定一个主题。
2. 迭代推断：重复以下步骤直到收敛：
   • 对于每个文档中的每个单词，根据当前的主题分布和单词分布计算该单词属于每个主题的概率。
   • 根据计算得到的概率，重新采样每个单词的主题。
3. 输出结果：根据推断得到的主题分布和单词分布，可以得到每个文档的主题分布以及每个主题的单词分布作为模型的输出结果。

2-1-23. Word2Vec和LDA

• 区别：

  • Word2Vec是一种基于神经网络的词向量表示方法，通过学习词语的分布式表示来捕捉词语之间的语义关系。它关注的是词语之间的相似性和语义含义。

  • LDA是一种概率生成模型，用于解释文档的主题结构。它关注的是文档中的主题分布和主题的单词分布。

• 联系：

  • Word2Vec和LDA都是无监督学习方法，可以从大规模未标注的文本数据中学习语义信息。

  • Word2Vec可以用于词语相似度计算、文本分类等任务，而LDA可以用于主题分析、文本聚类等任务。

  • Word2Vec可以提供每个词语的向量表示，而LDA可以提供每个文档的主题分布和每个主题的单词分布。

2-1-24. SKip-gram和cbow

Skip-gram和CBOW是Word2Vec模型中的两种不同训练方法，它们在模型结构和训练过程上有一些异同。

• 相同点：

  • Skip-gram和CBOW都是用于学习词向量表示的方法，通过预测上下文或目标词语来训练模型。

  • 它们都使用了一个浅层神经网络模型，包括输入层、投影层和输出层。

• 不同点：

  • Skip-gram模型的目标是根据目标词语来预测上下文词语，即从目标词语生成上下文词语。而CBOW模型的目标是根据上下文词语来预测目标词语，即从上下文词语生成目标词语。

  • Skip-gram模型适用于较大的语料库，能够更好地捕捉罕见词语的语义信息。CBOW模型在小型语料库上的训练速度更快，但对于常见词语的表示效果较好。

  • Skip-gram模型在训练过程中会考虑更多的上下文信息，因此在语料库较大时能够学习到更多的语义信息。CBOW模型在训练过程中会对上下文中的词语进行平均，因此对于频繁出现的词语有更好的表示能力。

2-1-25. 图像数据数据

1. 读取图像：使用图像处理库（如OpenCV）读取图像文件，并将其加载到内存中。
2. 预处理：对图像进行预处理操作，以提高后续分析的效果。预处理操作可以包括图像的缩放、裁剪、旋转、去噪等。
3. 特征提取：从图像中提取有用的特征，以表示图像的内容。常用的图像特征提取方法包括：
   • 颜色特征：提取图像的颜色直方图、颜色矩、颜色梯度等。
   • 纹理特征：提取图像的纹理信息，如灰度共生矩阵、Gabor滤波器响应等。
   • 形状特征：提取图像的形状信息，如边缘检测、轮廓提取、角点检测等。
   • 深度学习特征：使用预训练的深度学习模型（如卷积神经网络）提取图像的高级语义特征。
4. 特征表示：将提取到的特征表示为数值向量或特征描述子。通常使用固定长度的向量表示图像特征，如使用主成分分析（PCA）或局部二值模式（LBP）等方法进行降维。
5. 分析和应用：基于提取到的图像特征，可以进行各种图像分析和应用，如图像分类、目标检测、图像检索、图像生成等。

​ 常用的图像特征提取方法还包括HOG（方向梯度直方图）、SIFT（尺度不变特征变换）、SURF（加速稳健特征）等。选择合适的特征提取方法取决于具体的应用场景和需求。

2-1-26. 特征选择、卡方校验、信息值、VOE

• 从给定的特征集合中选出相关特征子集的过程称作特征选择feature selection，进行特征选择的原因：

  • 首先，在现实任务中经常会遇到维数灾难问题，这是由于属性过多造成的。如果能从中选择出重要的特征，使得后续学习过程仅仅需要在一部分特征上构建模型，则维数灾难问题会大大减轻。

    从这个意义上讲，特征选择与降维技术有相似的动机。事实上它们是处理高维数据的两大主流技术。

  • 其次，去除不相关特征往往会降低学习任务的难度。

• 要想从初始的特征集合中选取一个包含了所有重要信息的特征子集，如果没有任何领域知识作为先验假设，则只能遍历所有可能的特征组合。这在计算上是不可行的，因为这样会遭遇组合爆炸，特征数量稍多就无法进行。一个可选的方案是：

  • 产生一个候选子集，评价出它的好坏。

  • 基于评价结果产生下一个候选子集，再评价其好坏。

  • 这个过程持续进行下去，直至无法找到更好的后续子集为止。

• 常见的特征选择方法大致可分为三类：过滤式filter、包裹式wrapper、嵌入式embedding 。

  • 过滤式选择：过滤式方法先对数据集进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关。这相当于先用特征选择过程对初始特征进行过滤，再用过滤后的特征来训练模型。
  • 包裹式选择：与过滤式特征选择不考虑后续学习器不同，包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价准则。其目的就是为给定学习器选择最有利于其性能、量身定做的特征子集。LVW算法中使用随机策略来进行子集搜索。优点：由于直接针对特定学习器进行优化，因此从最终学习器性能来看，效果比过滤式特征选择更好。缺点：需要多次训练学习器，因此计算开销通常比过滤式特征选择大得多。
  • 嵌入式选择：嵌入式特征选择是将特征选择与学习器训练过程融为一体，两者在同一个优化过程中完成的。即学习器训练过程中自动进行了特征选择。
    • 以线性回归模型为例。引入 $L_1$ 范数（lasso回归）除了降低过拟合风险之外，还有一个好处：它求得的 $\overrightarrow{\mathbf{w}}$ 会有较多的分量为零。即：它更容易获得稀疏解。
    • 于是基于 $L_1$ 正则化的学习方法就是一种嵌入式特征选择方法，其特征选择过程与学习器训练过程融为一体，二者同时完成。
    • $\overrightarrow{\mathrm{w}}$取得稀疏解意味着初始的d个特征中仅有对应着$\overrightarrow{\mathrm{w}}$的非零分量的特征才会出现在最终模型中。$L_1$ 正则化问题的求解可以用近端梯度下降Proximal Gradient Descent:PGD算法求解。

2-1-27. 特征相关性计算方法和优缺点

计算特征之间的相关性可以使用多种方法，以下是几种常见的方法及其优缺点：

• 相关系数（如Pearson相关系数）：用于度量线性关系的强度和方向。它的取值范围在-1到1之间，可以判断特征之间的线性相关性。优点是简单易计算，缺点是只能捕捉线性相关性。
• 互信息（Mutual Information）：用于度量特征之间的相互依赖程度。它可以捕捉特征之间的任意关系，包括线性和非线性关
• 斯皮尔曼相关系数（Spearman’s Rank Correlation Coefficient）：与Pearson相关系数类似，但是它是基于变量的秩次而不是实际值。它可以捕捉到非线性的关系，并且对于异常值不敏感。
• 判定系数（Coefficient of Determination）：用于衡量一个特征能够通过线性回归模型来解释另一个特征的变异程度。判定系数的取值范围在0到1之间，越接近1表示两个特征之间的线性关系越强。
• 距离相关性（Distance Correlation）：通过测量特征之间的距离来评估它们之间的相关性。距离相关性可以捕捉到任意形式的关系，包括线性和非线性关系。
• 互信息增益（Mutual Information Gain）：用于评估一个特征对于目标变量的信息增益。它衡量了一个特征能够提供关于目标变量的额外信息量。

每种方法都有其适用的场景和限制。选择合适的方法取决于数据的特征性质、问题的要求以及所需的计算效率。在进行特征选择或特征工程时，可以结合多种方法来综合评估特征之间的相关性，以获得更全面的信息。

2-2. KNN

KNN Introduction

2-2-1. KNN建模流程

KNN（K-最近邻）建模流程如下：

1. 准备数据集：收集带有标签的训练样本数据。
2. 选择K值：确定K值，即要考虑的最近邻居的数量。
3. 计算距离：使用适当的距离度量（如欧氏距离、曼哈顿距离等），计算每个测试样本与训练集中所有样本之间的距离。
4. 选择邻居：根据计算得到的距离，选择与测试样本最近的K个训练样本作为邻居。
5. 进行投票或计算平均值：根据分类问题或回归问题，对K个邻居的标签进行投票或计算平均值。
6. 预测结果：根据投票结果或平均值，将测试样本归类或预测其值。

（1）根据给定的距离度量，在训练集 $T$ 中找出与 $x$ 最邻近的 $k$个点，涵盖这 $k$ 个点的邻域记作 $N_k(x)$；

（2）在$N_k(x)$中根据分类决策规则（如多数表决）决定 $x$ 的类别 $y$：
$$
y=\arg \max {c{j}} \sum_{x_{i} \in N_{k}(x)} I\left(y_{i}=c_{j}\right), \quad i=1,2, \cdots, N_{i} \quad j=1,2, \cdots, K
$$
在上式中，$I$为指示函数，即当$y_{i}=c_{j}$时为1，否则为0。

2-2-2. KNN优缺点

• knn优点：

  1. 理论成熟，思想简单，既可以用来做分类又可以做回归

  2. KNN是一种在线技术，新数据可以直接加入数据集而不必进行重新训练

  3. 可用于非线性分类（数据集不要求线性可分）

  4. 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感

• knn缺点：

  1. 计算量大，尤其是数据集非常大的时候
  2. 样本不平衡的时候，对稀有类别的预测准确率低
  3. KD树，球树之类的模型建立需要大量的内存
  4. k值大小的选择很重要

2-2-3. KNN适用场景和数据类型

• KNN适合以下场景和数据类型：

  • 小规模或中等规模的数据集。

  • 非线性数据，特别是当类别之间的决策边界不规则或复杂时。

  • 类别分布均衡的数据集。

通常最近邻分类器使用于特征与目标类之间的关系为比较复杂的数字类型，或者说二者关系难以理解，但是相似类间特征总是相似。数据要求归一化，统一各个特征的量纲。

2-2-4. 常用的距离衡量公式、计算流程、使用场景

1. 闵可夫斯基距离

特征空间 $\mathcal X$ 是n维实数向量空间 $\mathbf{R}^n$ ，$x_i,x_j\in \mathcal{X}, x_i = (x_i^{(1)}, x_i^{(2)},\cdots x_i^{(n)} ), x_j = (x_j^{(1)}, x_j^{(2)}, \cdots, x_j^{(n)})$ 。则 $x_i,x_j$的 $L_p$距离（闵可夫斯基距离）定义为
$$
L_p(x_i, x_j) = (\sum_{l=1}^n |x_i^{(l)}-x_j^{(l)}|)^{\frac{1}{p}}
$$
这里 $p \geq 1 $。

2. 欧式距离

当 $p=2$时，称为欧氏距离，强调数值上的绝对误差

是严格定义的距离，满足正定性、对称性、三角不等式
$$
L_2(x_i, x_j) = (\sum_{l=1}^n |x_i^{(l)}-x_j^{(l)}|)^{\frac{1}{p}}
$$
3. 曼哈顿距离（p=1）

$$
L_1(x_i, x_j) = \sum_{l=1}^n |x_i^{(l)}-x_j^{(l)}|
$$
4. 切比雪夫距离（$p = \infty$），各个坐标距离数值差的绝对值的最大值

$$
L_{\infty}(x_i, x_j) = \mathop{\max}_{l} \ |x_i^{(l)}-x_j^{(l)}|
$$
5. 马氏距离

考虑各个分量（特征）之间的相关性并与各个分量的尺度无关。给定一个样本集合$X$，$X=(x_{ij}){m\times n}$，其协方差矩阵记为$S$。样本$x_i$与样本$x_j$之间的马氏距离$d{ij}$定义为
$$
d_{ij} = [(x_i - x_j)^TS^{-1}(x_i - x_j)]^{\frac{1}{2}}
$$
当$S$为单位矩阵时，即样本数据的各个分量互相独立且各个分量的方差为1时，马氏距离就是欧氏距离。

6. 汉明距离

两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数

1011101 与 1001001 之间的汉明距离是 2。

2143896 与 2233796 之间的汉明距离是 3。

“toned” 与 “roses” 之间的汉明距离是 3。

7. 相关系数（correlation coefficient）

相关系数的绝对值越接近1，表示样本越相似；越接近0，表示样本越不相似。

$x_i$与$x_j$之间的相关系数定义为
$$
r_{ij} =
\frac{\sum_{k=1}^{m}\left(x_{k i}-\overline{x}{i}\right)\left(x{k j}-\overline{x}{j}\right)}{\left[\sum{k=1}^{m}\left(x_{k i}-\overline{x}{i}\right)^{2} \sum{k=1}^{m}\left(x_{k j}-\overline{x}_{j}\right)^{2}\right]^{\frac{1}{2}}}
$$

$$
\overline{x}{i}=\frac{1}{m} \sum{k=1}^{m} x_{k i}, \quad \overline{x}{j}=\frac{1}{m} \sum{k=1}^{m} x_{k j}
$$

8. 余弦相似度

强调方向上的相对误差

不是严格定义的距离，满足正定性、对称性，不满足三角不等式
$$
cos(A,B) = \frac{A \cdot B}{||A||_2 ||B||_2}
$$
9. KL散度

计算两个分布的差异性

不是严格定义的距离，满足正定性，不满足对称性、三角不等式

使用场景

• 欧氏距离：适用于向量各分量的度量标准统一的情况；当某些特征比其他特征取值大很多时，精确度会变差，很多特征值为0，即稀疏矩阵，结果不准，数据点的分布是某个圆心的半径，用欧式距离就不能比较了。
• 曼哈顿距离：适用于计算类似街区距离这样的实际问题。异常值对分类结果影响比欧式距离小。量纲不同时使用曼哈顿距离比欧式距离好。

总结

用距离度量相似度时，距离越小样本越相似；用相关系数时，相关系数越大样本越相似。

2-2-5. 超参数K值

超参数K值过大或过小都会对结果产生影响：

• 当K值较小（如1）时，模型对局部噪声敏感，可能导致过拟合。
• 当K值较大时，模型的平滑性增加，可能导致欠拟合。

选择适当的K值一般通过交叉验证或网格搜索来确定，常用的方法包括：

• 网格搜索：尝试不同的K值，比较它们在验证集上的性能指标（如准确率、F1分数等），选择表现最好的K值。
• 交叉验证：将训练集划分为多个子集，在每个子集上进行训练和验证，计算平均性能指标，选择平均性能最好的K值。

​ 如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

​ 如果选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

​ K=N，则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的累，模型过于简单，忽略了训练实例中大量有用信息。

​ 在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。

2-2-6. Kd树

Kd树是一种用于加速KNN搜索的数据结构。建树和搜索最近节点的过程如下：

建树过程：

1. 选择一个维度：从样本中选择一个维度作为划分依据。
2. 选择划分点：在选择的维度上，选择一个划分点，可以是中位数或其他分位点。
3. 划分数据集：将样本集根据划分点划分为两个子集，小于等于划分点的样本划入左子树，大于划分点的样本划入右子树。
4. 递归构建：对左右子树分别递归执行以上步骤，直到每个子集只含有一个样本或为空集。

搜索最近节点过程：

1. 初始化：从根节点开始，将目标样本作为当前最近节点。
2. 遍历树：从根节点开始，根据目标样本在当前维度上的值与划分点的关系，选择相应的子树进行遍历。
3. 更新最近节点：在遍历过程中，计算目标样本与当前节点的距离，并更新最近节点和最近距离。
4. 回溯：在遍历到叶子节点或者到达根节点时，回溯到父节点，并继续遍历其他子树。
5. 剪枝：如果当前节点距离目标样本的距离大于最近距离，可以跳过该子树的遍历。

通过建立Kd树，可以减少搜索的样本数量，提高KNN搜索的效率。

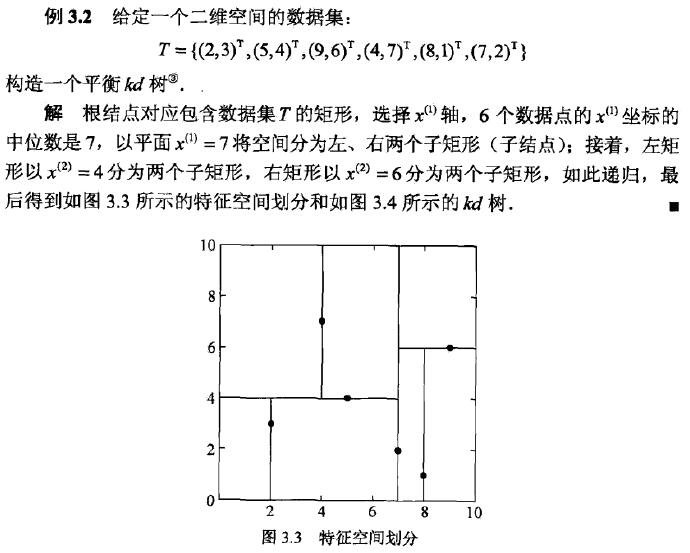
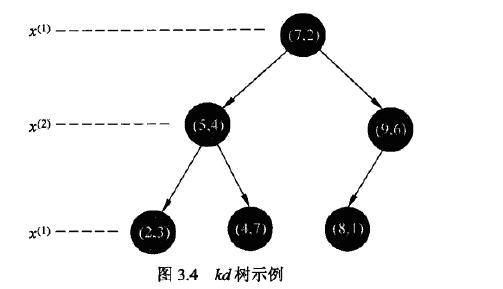
kd树是一种对k维空间中的实例点进行存储，以便对其进行快速检索的树形数据结构。kd树是二叉树，表示对k维空间的一个划分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。kd树的每个节点对应于一个k维超矩形区域。

构造平衡kd树过程：

输入：k维空间数据集 $T=\left{x_{1}, x_{2}, \cdots, x_{N}\right}$，其中$x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \cdots, x_{i}^{(k)}\right)^{\mathrm{T}}, \quad i=1,2, \cdots, N_{\mathrm{i}}$

输出：kd树

（1）开始：构造根节点，根节点对应于包含T的k维空间的超矩形区域

​ 选择 $x^{(1)} $ 为坐标轴，以T中所有实例的 $x^{(1)} $ 坐标的中位数为切分点，将根节点对应的超矩形区域且分为两个子区域。切分由通过切分点并与坐标轴 $x^{(1)}$垂直的超平面实现。

​ 由根节点生成深度为1的左、右子节点：左子节点对应坐标 $x^{(1)}$小于切分点的子区域，右子节点对应于坐标 $x^{(1)}$ 大于切分点的子区域。

​ 将落在切分超平面上的实例点保存在根节点。

（2）重复：对深度为$j$ 的节点，选择 $x^{(l)}$ 为切分的坐标轴，$l = j({\rm mod}\ k) + 1$，以该节点的区域中所有实例的 $x^{(l)}$ 坐标的中位数为切分点，将该节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 $x^{(l)}$垂直的超平面实现。

​ 由该节点生成深度为 $j+1$ 的左、右子节点：左子节点对应坐标 $x^{(l)}$小于切分点的子区域，右子节点对应坐标$x^{(l)}$大于切分点的子区域。

​ 将落在切分超平面上的实例点保存在根节点。

（3）直到两个子区域没有实例存在时停止，从而形成kd树的区域划分

算法：用kd树的最近邻搜索

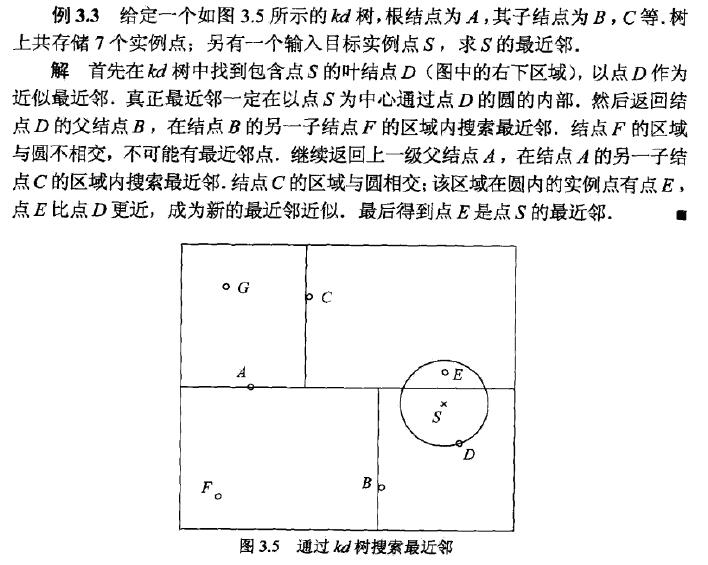
输入：已构造的kd树：目标点$x$；

输出：$x$的最近邻

（1）在kd树中找出包含目标点$x$的叶节点：从根节点出发，递归地向下访问kd树。若目标点$x$当前维的坐标小于切分点的坐标，则移动到左子节点，否则移动到右子节点。直到子节点为叶节点为止。

（2）以此叶节点为“当前最近点”。

（3）递归地向上回退，在每个节点进行以下操作：

​ （a）如果该节点保存的实例点比当前最近点距离目标点更近，则以该实例点作为“当前最近点”

​ （b）当前最近点一定存在于该节点一个子节点对应的区域。检查该子节点的父节点的另一子节点（兄弟节点）对应区域是否有更近的点。具体地，检查另一子节点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交。

​ 如果相交，可能在另一个子节点对应的区域内存在距目标点更近的点，移动到另一个子节点。接着递归地进行最近邻搜索；

​ 如果不相交，向上回退

（4）当回退到根节点时，搜索结束。最后的“当前最近点”即为$x$的最近邻点。

如果实例点是随机分布的，kd树搜索的平均计算复杂度是 $O({\rm log} N)$，这里 $N$ 是训练实例数。kd树更适用与训练实例数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时，它的效率会迅速下降，几乎接近线性扫描。

2-3. SVM

SVM Introduction-1, SVM Introduction-2, SVM Introduction-3

• Maximum Margin Classifier(基本模型,hard margin) => Support Vector Classifier(SVC,soft margin) => Support Vector Machine(SVM)
• SVM = SVC + 非线性核函数

2-3-1. SVM模型原理

SVM（支持向量机）是一种用于二分类和多分类问题的监督学习模型。其原理可以简要概括如下：

1. 定义超平面：SVM的目标是找到一个超平面，将特征空间中的样本点分为不同的类别。对于二分类问题，超平面可以表示为 w·x + b = 0，其中 w 是法向量，b 是偏置项。
2. 最大化间隔：SVM的目标是找到具有最大间隔的超平面，即使得样本点与超平面之间的距离最大化。这样可以提高模型的泛化能力。
3. 支持向量：在最大化间隔的过程中，只有少数样本点位于最大间隔边界上，它们被称为支持向量。这些支持向量决定了超平面的位置。
4. 核函数：SVM可以通过引入核函数将非线性问题映射到高维特征空间，使得样本在高维空间中线性可分。这样可以处理非线性问题。

• Maximum Margin Classifier的缺陷：
  • 由于SVM尽量把所有的样本都分开，一条新数据，决策边界可能有巨大的改变。
  • 数据线性线性不可分的时候，找不到决策边界。
• 支持向量机是是一种二类分类模型，它的基本模型是是定义在特征空间的间隔最大的线性分类器，间隔最大，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略是间隔最大化，可形式化为求解凸二次规划的问题，也等价于正则化的合页损失函数最小化问题。
  • 线性可分支持向量机：当训练数据线性可分，通过硬间隔最大化，学习一个线性的分类器
  • 线性支持向量机：当训练数据近似线性可分，通过软间隔最大化，学习一个线性的分类器
  • 非线性支持向量机：当训练数据线性不可分，通过使用核技巧及软间隔最大化，学习非线性分类器

2-3-2. 缺失值敏感原因、处理方法

SVM对缺失值敏感的原因是，SVM的优化算法依赖于样本之间的距离计算，而缺失值会干扰距离计算的准确性。

处理缺失值的方法有多种：

• 删除含有缺失值的样本：如果缺失值的比例较小，可以选择删除含有缺失值的样本。
• 填充缺失值：可以使用均值、中位数、众数等统计量填充缺失值，或者使用插值方法进行填充。
• 考虑缺失值作为新的特征：将缺失值作为一个新的特征引入模型中，赋予其特定的值（如0或1），表示样本是否存在缺失值。

具体选择哪种方法取决于数据集的特点和缺失值的分布情况。

涉及到距离度量(distance measurement)时，如计算两个点之间的距离，缺失数据就变得比较重要。如果缺失值处理不当就会导致效果很差，如SVM，KNN。常用的缺失值处理方法：

（1）把数值型变量(numerical variables)中的缺失值用其所对应的类别中(class)的中位数(median)替换。把描述型变量(categorical variables)缺失的部分用所对应类别中出现最多的数值替代(most frequent non-missing value)。【快速简单但效果差】（平均数、中位数、众数、插值等）

（2）将缺失值当成新的数值，NaN

（3）忽略该项数据（当缺失少时）

2-3-3. SVM分类非线性问题

SVM可以通过引入核函数将非线性问题映射到高维特征空间，使得样本在高维空间中线性可分。这是因为在高维空间中，数据可以通过超平面进行线性划分，即使在原始特征空间中是非线性可分的。

原输入空间是一个非线性可分问题，能用一个超曲面将正负例正确分开；

通过核技巧的非线性映射，将输入空间的超曲面转化为特征空间的超平面，原空间的非线性可分问题就变成了新空间的的线性可分问题。低维映射到高维。

在核函数 $K(x,z)$ 给定的条件下，可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在特征空间进行的，在学习和预测中只定义核函数 $K(x,z)$，而不需要显式地定义特征空间和映射函数$\phi$，这样的技巧称为核技巧。通常直接计算$K(x,z)$比较容易，而通过$\phi(x)$和$\phi(z)$计算$K(x,z)$并不容易。对于给定核 $K(x,z)$，特征空间和映射函数的取法并不唯一。

2-3-4. 常用的核函数、选择核函数

常用的核函数包括：

• 线性核函数（Linear Kernel）：K(x, y) = x·y，对应于线性SVM，适用于线性可分问题。
• 多项式核函数（Polynomial Kernel）：K(x, y) = (x·y + c)^d，其中 c 和 d 是超参数，适用于多项式可分问题。
• 高斯径向基函数核（RBF Kernel）：K(x, y) = exp(-gamma * ||x-y||^2)，其中 gamma 是超参数，适用于非线性可分问题。

选择不同的核函数取决于数据集的特点和问题的复杂度。一般来说，线性核函数适用于线性可分问题，多项式核函数适用于一定程度的非线性问题，而高斯径向基函数核适用于更复杂的非线性问题。

• 核函数定义：设$\mathcal{X}$是输入空间，又设$\mathcal{H}$为特征空间，如果存在一个从$\mathcal{X}$到$\mathcal{H}$的映射

$$
\phi(x) : \mathcal{X} \rightarrow \mathcal{H}
$$

​ 使得对所有$x, z \in \mathcal{X}$，函数$K(x, z)$满足条件
$$
K(x, z)=\phi(x) \cdot \phi(z)
$$
​ 则称$K(x, z)$为核函数，$\phi(x)$为映射函数，式中$\phi(x) \cdot \phi(z)$$为\phi(x)$和$\phi(z)$的内积

• 线性核函数

$$
K(x,z) = x\cdot z
$$

​ 主要用于线性可分的情况。可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的。

• 多项式核函数（polynomial kernel function）

$$
K(x, z)=(x \cdot z+1)^{p}
$$

​ 对应的支持向量机是一个p次多项式分类器。分类决策函数为
$$
f(x)=\operatorname{sign}\left(\sum_{i=1}^{N_{s}} a_{i}^{} y_{i}\left(x_{i} \cdot x+1\right)^{p}+b^{}\right)
$$
​ 多项式核函数可以实现将低维的输入空间映射到高维的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。

• 高斯核函数（Gaussian kernel function）

$$
K(x,z) = exp(-\frac{1}{2} \ ||x - z ||_2 ) = \phi(x) \cdot \phi(z)
$$

​ 对应的支持向量机是高斯径向基函数（radial basis function）分类器，分类决策函数为
$$
f(x)=\operatorname{sign}\left(\sum_{i=1}^{N_{s}} a_{i}^{} y_{i} \exp \left(-\frac{|x-x_i|^{2}}{2 \sigma^{2}}\right)+b^{}\right)
$$
​ 高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。

• Sigmod核函数

$$
K\left(x, z\right)=\tanh \left(\eta \ x \cdot z +\theta\right)
$$

总结

• 如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM, (特征维度高，往往线性可分，SVM解决非线性分类问题的思路就是将样本映射到更高维的特征空间中)
• 如果样本数量很多，由于求解最优化问题的时候，目标函数涉及两两样本计算内积，使用高斯核明显计算量会大于线性核，所以手动添加一些特征，使得线性可分，然后可以用LR或者线性核的SVM
• 如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；

2-3-5. RBF核函数

根据Cover定理，从低维度映射到高维度后，线性可分的可能性比较大。RBF核函数并不一定线性可分，因为RBF核函数可以将数据映射到无穷维的特征空间，即使在无穷维的空间中，仍然存在一些数据分布是不可分的。

而RBF核函数将原始空间映射到无穷维的特征空间，基本线性可分（也有线性不可分的情况，如加入噪声：同一样本不同标签）。如果忽略噪声，同时允许一定限度的误差，可以说升到足够高的维度，几乎所有数据集都是线性可分了。

同时，维度特别高，几乎一定线性可分，也以为这模型特别复杂，几乎一定会碰到过拟合问题。

2-3-6. SVM模型线性性

基本模型是一个线性分类器；而通过使用核函数可以学习非线性支持向量机

2-3-7. 训练误差为0的SVM

训练误差为0的SVM分类器并不一定存在。这是因为SVM的目标是找到具有最大间隔的超平面来分隔样本，而不仅仅是追求训练误差为0。在训练样本线性可分的情况下，存在至少一个能够将样本完全正确分类的超平面，此时训练误差可以为0。然而，在训练样本中存在噪声或样本本身不可分的情况下，训练误差为0的分类器可能不存在。此时，SVM的目标是在最大化间隔的同时尽量减少分类误差，找到一个最优的分类器。

对于训练一个不加入松弛变量的SVM模型时，一定存在。百面p55，对于加入松弛变量的SVM的训练误差不一定能达到0

2-3-8. 支持向量数量

结论：在n维特征空间中，线性SVM一般会产生n+1个支持向量（不考虑退化情况）

通常的SVM的使用会伴随着核技巧（kernel），这用于将低维空间映射到一个更高维的空间，使得原本不线性可分的数据点变得在高维空间中线性可分。虽然这种映射是隐式的，我们通常并不知道映射到的空间是什么样子。但是根据之前的结论，我们可以认为如果训练出来的SVM有d+1个支持向量，这个kernel在这个任务里就讲原来的数据映射到了一个d维的空间中，并使得其线性可分。

更高的维度通常意味着更高的模型复杂度，所以支持向量越多，表示着训练得到的模型越复杂。根据泛化理论，这意味着更有过拟合的风险。

如果在性能一致的情况下，更少的支持向量可能是更好的。但是这一点其实不绝对，因为泛化理论仅仅是误差的上界，实际的泛化情况的决定因素比较复杂，也可能取决于kernel的性质。所以还是自己做cross validation比较好。

2-3-9. 多类分类问题

1. 某些算法原生的支持多分类，如：决策树、最近邻算法等。但是有些算法只能求解二分类问题，如：支持向量机。

2. 对于只能求解二分类问题的算法，一旦遇到问题是多类别的，那么可以将多分类问题拆解成二分类任务求解。

   即：

   • 先对原问题进行拆分，然后为拆出的每个二分类任务训练一个分类器。
   • 测试时，对这些二分类器的预测结果进行集成，从而获得最终的多分类结果。

3. 多分类问题有三种拆解方式：

   • 一对其余(One-vs-rest:OvR) 。

     • 为每一对类别训练一个分类器。

   • 一对一(one-vs-one:OvO) 。

     • 训练k(k-1)个分类器

   • 多对多(many-vs-many:MvM) 。

2-4. 朴素贝叶斯

2-4-1. 贝叶斯定理

$$
P\left(B_{i} | A\right)=\frac{P\left(B_{i}\right) P\left(A | B_{i}\right)}{\sum_{j=1}^{n} P\left(B_{j}\right) P\left(A | B_{j}\right)}
$$

2-4-2. 条件概率、边缘概率、联合概率

条件概率：条件概率表示在条件$Y=b$成立的情况下，$X=a$的概率，记作$P(X=a|Y=b)$或$P(a|b)$。它具有如下性质： “在条件Y=b下X的条件分布”也是一种“X的概率分布”，因此穷举X的可取值之后，所有这些值对应的概率之和为1 即：
$$
\sum_{a} P(X=a | Y=b)=1
$$
边缘概率：仅与单个随机变量有关的概率称为边缘概率，如 $P(X=a)$ 或 $P(Y=b)$

联合概率：联合概率指的是包含多个条件且所有条件同时成立的概率，记作$P(X=a,Y=b)$或$P(a,b)$

联合概率、边缘概率与条件概率的关系：
$$
P(X=a | Y=b)=\frac{P(X=a, Y=b)}{P(Y=b)}
$$

2-4-3. 后验概率最大化

朴素贝叶斯法将实例分到后验概率最大的类中。后验概率最大化这等价于期望风险最小化。假设选择0-1损失函数：
$$
L(Y, f(X))=\left{\begin{array}{ll}{1,} & {Y \neq f(X)} \ {0,} & {Y=f(X)}\end{array}\right.
$$
其中 $f(X)$是分类决策函数。这是期望风险函数为
$$
R_{\operatorname{cap}}(f)=E[L(Y, f(X))]
$$
期望是对联合分布 $P(X,Y)$ 取的。由此取条件期望
$$
R_{\mathrm{exp}}(f)=E_{X} \sum_{k=1}^{K}\left[L\left(c_{k}, f(X)\right)\right] P\left(c_{k} | X\right)
$$
为了使期望奉献最小化，只需对 $X=x$ 逐个最小化，由此得到
$$
\begin{aligned} f(x) &=\arg \min {y \in \mathcal{Y}} \sum{k=1}^{K} L\left(c_{k}, y\right) P\left(c_{k} | X=x\right) \ &=\arg \min {y \in \mathcal{Y}} \sum{k=1}^{K} P\left(y \neq c_{k} | X=x\right) \ &=\arg \min {y \in \mathcal{Y}}\left(1-P\left(y=c{k} | X=x\right)\right) \ &=\arg \max {y \in \mathcal{Y}} P\left(y=c{k} | X=x\right) \end{aligned}
$$
这样一来，根据期望风险最小化准则就得到了后延概率最大化准则：
$$
f(x)=\arg \max {c{k}} P\left(c_{k} | X=x\right)
$$
即朴素贝叶斯法所采用原理

2-4-4. 朴素贝叶斯的学习和训练

对于给定的训练数据集，首先基于特征条件独立性假设学习输入输出的联合概率分布；

训练过程：

（1）计算先验概率及条件概率
$$
\begin{array}{l}{P\left(Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)}{N}, \quad k=1,2, \cdots, K} \ {P\left(X^{(j)}=a_{j l} | Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j}, y_{i}=c_{k}\right)}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)}} \ {j=1,2, \cdots, n ; \quad l=1,2, \cdots, S_{j} ; \quad k=1,2, \cdots, K}\end{array}
$$
（2）对于给定实例 $x=\left(x^{(1)}, x^{(2)}, \cdots, x^{(n)}\right)^{\mathrm{T}}$，计算
$$
P\left(Y=c_{k}\right) \prod_{i=1}^{n} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right), \quad k=1,2, \cdots, K
$$
（3）确定实例x的类（最大后验概率）
$$
y = \arg\max_{c_k}\ P(Y=c_k)\prod_{j}P(X^{(j)}=x^{(j)}|Y=c_k)
$$

2-4-5. 生成模型和判别模型

• 生成模型

  • 生成方法由数据学习联合概率分布 $P(X,Y)$，然后求出条件概率分布 $P(Y|X)$作为预测模型：
    $$
    P(Y|X) = \frac{P(X,Y)}{P(X)}
    $$
    之所以成为生成方法，是因为模型表示了给定输入 $X$ 产生输出 $Y$的生成关系。

    典型的生成模型：朴素贝叶斯法、隐马尔可夫模型。

• 判别模型

  • 判别方法由数据直接学习决策函数 $f(X)$ 或者条件概率分布 $P(X,Y)$作为预测的模型，关心的是对给定的输入 $X$，应该预测什么样的输出 $Y$。
  • 典型的判别模型：k近邻、感知机、决策树、逻辑斯蒂回归、最大熵模型、支持向量机、提升方法、条件随机场。

感觉本质上就是，是不是从概率论的角度，表征事件。下面这些没有明确follow概率论，上面是明确用概率论对于数据进行的建模。

2-4-6. 朴素？存在问题与优化方向

“朴素”体现在朴素贝叶斯模型对条件概率分布作了条件独立性假设，这是一个较强的假设。
$$
\begin{aligned} P(X&=x | Y=c_{k} )=P\left(X^{(1)}=x^{(1)}, \cdots, X^{(n)}=x^{(n)} | Y=c_{k}\right) \ &=\prod_{j=1}^{n} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right) \end{aligned}
$$
存在问题：当特征分布不满足条件独立性假设时，分类的性能不高

优化方法：贝叶斯网络

2-4-7. 贝叶斯网络

朴素贝叶斯法假设输入变量都是条件独立的，如果假设他们之间存在概率依存关系，模型就被成了贝叶斯网络。

贝叶斯网络也称为“信念网”，借助有向无环图来刻画属性之间的依赖关系，并使用条件概率表来描述属性的联合概率分布。贝叶斯网结构有效地表达了属性的条件独立性。

具体来说，一个贝叶斯网B由结构G和参数 $\theta$ 表示，即 $B = <G,\theta>$ 。网络结构G是一个有向无环图，其每个节点对应于一个属性，若两个属性有直接依赖关系，则它们由一条边连接起来；参数 $\theta$ 定量描述这种依赖关系，假设属性 $x_i$ 在G中的父节点集为 $\pi_i$，则 $\theta$包含了每个属性的条件概率 $\theta_{x_i|\pi_i} = P_B(x_i|\pi_i)$。给定父节点集，贝叶斯网假设每个属性与它的非后裔属性独立，于是将属性的联合概率分布定义为

$$
P_{B}\left(x_{1}, x_{2}, \ldots, x_{d}\right)=\prod_{i=1}^{d} P_{B}\left(x_{i} | \pi_{i}\right)=\prod_{i=1}^{d} \theta_{x_{i} | \pi_{i}}以上图为例，联合概率分布定义为
$$

$$
P\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=P\left(x_{1}\right) P\left(x_{2}\right) P\left(x_{3} | x_{1}\right) P\left(x_{4} | x_{1}, x_{2}\right) P\left(x_{5} | x_{2}\right)
$$

贝叶斯网学习过程：精确求解NP难，所以（1）贪心法：从某个网络结构出发，每次调整一条边，直到评分函数值不再降低（2）给网络结构施加约束条件：如限定为树形结构等。

贝叶斯网推断：理想情况根据贝叶斯网定义的联合概率分布来精确计算后验概率，但这样的精确推断时NP难的。近似推断采用吉布斯采样法，通过随机游走，使马尔可夫链趋于平稳分布。

2-4-8. 朴素贝叶斯是线性模型

线性分类器是通过特征的线性组合来做出分类决定的分类器。本质上，朴素贝叶斯分类器是一种线性分类器。

朴素贝叶斯分类器是建立在属性变量相互独立的基础上，后验概率为判定准则的分类器。不等式1成立，则样例x=[x_1,…,x_n]为正类。否则，样例为负类。

(1)

线性分类器直观地来说，是在高维样本空间中找到一组超平面，将样本空间划分了两个区域。每个区域对应于不同的类别。数学上来说，线性分类器能找到权值向量w，使得判别公式可以写成特征值的线性加权组合。

(2)

如果公式2成立，则样本属于正类；反之，则样本属于负类。

---

离散特征的朴素贝叶斯分类器

一般离散特征的取值范围有两种，{-1,1}或者{0,1}。这两种取值方式不会影响分析。不妨假设离散特征的取值范围为{-1,1}。下面的不等式成立，样例x=[x_1,…,x_n]为正类。
(3)

对于某个特征x，我们很容易推导出下面的公式

(4)

其中p(x|F)也有类似的结果，从而有
(5)

将公式5带入朴素贝叶斯分类器的公式3，得到下面的公式
(6)

根据公式6，离散特征的朴素贝叶斯分类器判别公式能够写成特征值的加权线性组合。也就是说，离散特征的朴素贝叶斯分类器本质上是线性分类器。

2-4-9. 如何解决用极大似然法可能出现所要估计的概率为0的情况

分子加1，分母加可能情况数

用极大似然法估计可能会出现所要估计的概率值为0的情况。这是会影响到后验概率的计算结果，使分类产生偏差。解决这一问题的方法是采用贝叶斯估计。具体地，条件概率的贝叶斯估计是
$$
P_{\lambda}\left(X^{(j)}=a_{j l} | Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j l}, y_{i}=c_{k}\right)+\lambda}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)+S_{j} \lambda}
$$
式中 $\lambda \geq 0$。等价于在随机变量各个取值的频数上赋予一个正数 $\lambda$。当$\lambda=0$时就是极大似然估计。常取 $\lambda=1$，这时称为拉普拉斯平滑（laplacian smoothing）。显然，对任何$l=1,2, \cdots, S_{j}, \quad k=1,2, \cdots, K$ 有
$$
\begin{array}{l}{P_{\lambda}\left(X^{(j)}=a_{j l} | Y=c_{k}\right)>0} \ {\sum_{l=1}^{s_{j}} P\left(X^{(j)}=a_{j l} | Y=c_{k}\right)=1}\end{array}
$$

表明上式确实为一种概率分布。同样，先验概率的贝叶斯估计是
$$
P_{\lambda}\left(Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)+\lambda}{N+K \lambda}
$$

2-5. 线性回归

2-5-1. 线性回归思想

线性回归的基本思想是通过建立一个线性模型来描述自变量（输入特征）与因变量（输出目标）之间的关系。它假设自变量与因变量之间存在一个线性关系，并通过找到最佳拟合的线性函数，以最小化预测值与实际观测值之间的差异。

2.5.2. 广义线性模型

线性回归是一种用于建立自变量与因变量之间线性关系的模型。它假设因变量与自变量之间存在一个线性关系，并通过最小化预测值与实际观测值之间的差异（通常使用平方损失函数）来找到最佳拟合的线性函数。

广义线性模型（Generalized Linear Model，GLM）是一种扩展的线性模型，适用于更广泛的因变量分布和非线性关系。广义线性模型通过引入一个链接函数（link function）将线性组合转换为非线性函数，从而能够适应不同的数据分布。例如，当因变量服从二项分布时，可以使用逻辑斯蒂回归模型，它使用逻辑斯蒂函数作为链接函数将线性组合映射到0和1之间的概率。

总结来说，线性回归是广义线性模型的一个特例，适用于连续数值预测并假设因变量与自变量之间存在线性关系。而广义线性模型可以适应更广泛的数据分布和非线性关系，通过选择合适的链接函数来描述因变量与自变量之间的关系。

2-5-3. 损失函数与优化算法

线性回归常用的损失函数有以下几种：

1. 平方损失函数（Mean Squared Error，MSE）：它是最常用的线性回归损失函数，计算预测值与真实值之间的差异的平方和。MSE可以表示为：$L(w, b) = \frac{1}{n} * \sum{(y - Xw - b)^2}$，其中y是真实值，X是自变量，w是权重向量，b是偏置项。
2. 绝对损失函数（Mean Absolute Error，MAE）：它计算预测值与真实值之间的差异的绝对值和，用于对异常值不敏感。MAE可以表示为：$L(w, b) = \frac{1}{n} * \sum |y - Xw - b|$。
3. Huber损失函数：它是平方损失函数和绝对损失函数的一种混合形式，对异常值具有鲁棒性。Huber损失函数可以表示为：$L(w, b) = \frac{1}{n} * \sum{H_{\delta}(y - Xw - b)}$，其中$H_{\delta}(z)$是Huber函数，当$|z| <= \delta$时为平方函数，当$|z| > \delta$时为线性函数。

常用的线性回归优化算法有以下几种：

1. 梯度下降法（Gradient Descent）：梯度下降法是一种迭代优化算法，通过计算损失函数关于参数的梯度方向，并以学习率的步长沿着梯度方向更新参数。常见的梯度下降法包括批梯度下降法（Batch Gradient Descent）、随机梯度下降法（Stochastic Gradient Descent）和小批量梯度下降法（Mini-Batch Gradient Descent）。
2. 正规方程法（Normal Equation）：正规方程法是一种闭式解法，通过求解线性方程组来直接计算最优参数。它通过求解$X^T Xw = X^T y$的正规方程，其中X是自变量矩阵，y是因变量向量。
3. 岭回归（Ridge Regression）：岭回归是一种正则化线性回归方法，通过在损失函数中添加L2正则项（对权重向量的平方和进行惩罚）来控制模型的复杂度。岭回归可以使用正规方程法求解，也可以使用梯度下降法进行优化。
4. Lasso回归（Lasso Regression）：Lasso回归是一种正则化线性回归方法，通过在损失函数中添加L1正则项（对权重向量的绝对值进行惩罚）来实现特征选择和稀疏性。Lasso回归通常使用最小角回归（LARS）算法或坐标下降算法进行优化。

这些是线性回归中常用的损失函数和优化算法，根据具体的问题和需求选择适合的损失函数和优化算法进行模型训练。

2-5-4. 线性回归适用问题及优缺点

• 线性回归适用于以下类型的问题：

  • 连续数值预测：线性回归可以用于预测因变量与自变量之间的线性关系，适用于连续数值的预测问题。例如，预测房屋价格、销售量等。
  • 关系分析：线性回归可以用于分析自变量与因变量之间的关系，并确定它们之间的线性趋势。这对于理解变量之间的相互作用和影响具有重要意义。

• 线性回归的优点包括：

  • 解释性强：线性回归提供了对模型的解释性，可以通过权重系数来理解自变量对因变量的影响程度。这有助于揭示变量之间的关系和作用机制。
  • 简单而高效：线性回归是一个简单而高效的模型，计算成本相对较低，而且对于大规模数据集也可以有效地应用。
  • 可解释性和稳定性：线性回归对异常值和噪声相对稳健，能够提供较为稳定的结果，并且对于数据的变化具有较好的解释能力。

• 线性回归的缺点包括：

  • 仅适用于线性关系：线性回归假设因变量与自变量之间存在线性关系，对于非线性关系的拟合能力较弱。当数据存在复杂的非线性关系时，线性回归可能无法提供准确的预测。
  • 对异常值敏感：线性回归对异常值敏感，异常值的存在可能会对模型的拟合产生较大的影响。需要对异常值进行处理或者采用鲁棒性更强的回归方法。
  • 特征选择的限制：线性回归对特征选择的能力有限，当存在大量特征或特征之间存在共线性时，可能需要额外的特征选择方法来提高模型的性能。

2-5-5. 最小二乘法估计线性回归模型的参数

• 当使用最小二乘法进行线性回归时，我们的目标是通过最小化平方损失函数来找到最佳的参数估计。最小二乘法的目标是使得预测值与实际观测值之间的残差平方和最小化。假设我们有一个包含m个样本的训练集，其中自变量表示为X，因变量表示为y。我们将自变量的第i个样本表示为X[i]，对应的因变量表示为y[i]。线性回归模型可以表示为：$y[i] = w^T * X[i] + b$，其中，w是权重向量，b是偏置项。我们的目标是找到最优的w和b来最小化平方损失函数：$L(w, b) = \frac{1}{2m} * \sum{(y[i] - (w^T * X[i] + b))^2}$

• 为了找到最小化损失函数的参数估计，我们需要对损失函数关于w和b分别求导，并令导数为0。具体推导如下

  • 对w求导$\frac{∂L}{∂w} = \frac{1}{m} * \sum{X[i] * (y[i] - (w^T * X[i] + b))} = 0$
    • 根据向量的性质，我们可以将上述求和式重写为矩阵形式：$\frac{∂L}{∂w} = \frac{1}{m} * X^T * (y - Xw - b) = 0$
    • 整理得到：$X^T * (y - Xw - b) = 0$
  • 对b求导：$\frac{∂L}{∂b} = \frac{1}{m} * \sum{y[i] - (w^T * X[i] + b)} = 0$
    • 根据向量的性质，我们可以将上述求和式重写为矩阵形式：$\frac{∂L}{∂b} = \frac{1}{m} * \sum{y - Xw - b} = 0$
    • 整理得到：$\sum{y - Xw - b}$ = 0

• 将上述两个方程合并，得到参数的更新公式：

$$
X^T * (y - Xw - b) = 0 \
\sum{y - Xw - b} = 0
$$

• 进一步整理得到：

$$
X^T * (y - Xw) = 0 \
\sum{y - Xw} = 0
$$

• 由于$X^T * X$和$X^T * y$是已知的，我们可以通过求解上述方程组来得到最优的参数估计：

$$
X^T * X * w = X^T * y \
\sum{Xw} = \sum{y}
$$

• 最终的参数估计可以通过解上述方程组得到：

$$
w = (X^T * X)^{(-1)} * X^T * y \
b = \frac{1}{m} * \sum{y - Xw}
$$

这就是使用最小二乘法进行线性回归时求解参数的更新公式。通过计算上述公式，我们可以得到最佳的参数估计，从而得到线性回归模型。

2-6. 逻辑回归

2-6-1. 逻辑回归v.s.线性回归

不同点：

• 逻辑回归处理的是分类问题，线性回归处理的是回归问题；
• 逻辑回归中认为y是因变量，即逻辑回归的因变量是离散的，线性回归的因变量是连续的。

相同点：

• 二者都使用了极大似然估计来对训练样本进行建模
• 求解超参数过程中，都可以使用梯度下降的方法

联系：

如果把一个事件的几率（odds）定义为该事件发生的概率与不发生概率的比值 $\frac{p}{1-p}$ ，那么逻辑回归可以看做是对于”y=1|x”这一事件的对数几率的线性回归
$$
{\rm log} \frac{p}{1-p} = \theta^{T}x ，其中\ p = P(y=1|x)
$$

2-6-2. 逻辑回归v.s.广义线性模型

逻辑回归是广义线性模型（Generalized Linear Model, GLM）的一种特例。广义线性模型是一类包括逻辑回归、线性回归等模型的统一框架，通过引入链接函数将线性模型的输出转化为非线性形式。可以看做广义线性模型在因变量y服从二元分布时的一个特殊情况。

2-6-3. 多标签分类

逻辑回归本质上是一个二分类模型，但可以通过一对多（One-vs-Rest）或一对一（One-vs-One）的方式进行多标签分类。在一对多方式中，对于每个标签，将其视为正类，其他标签视为负类，训练多个独立的逻辑回归模型。

如果一个样本只对应于一个标签（多分类问题）：
假设每个样本属于不同标签的概率服从几何分布，使用softmax regression进行分类：
$$
h_\theta =
\left[
\begin{matrix}
p(y=1|x;\theta)\
p(y=2|x;\theta) \
\vdots \
p(y=k|x;\theta)
\end{matrix}
\right]

\frac{1}{\sum_{j=1}^{k} e^{\theta^T x}}

\left[
\begin{matrix}
e^{\theta_1^T x}\
e^{\theta_2^T x} \
\vdots \
e^{\theta_k^T x}
\end{matrix}
\right]

\tag{3}
$$
其中 $\theta_1,\theta_2 \dots,\theta_k \in \mathbb{R}^n$

如果存在样本可能属于多个标签的情况时，可以训练k个二分类的逻辑回归分类器。第i个分类器用以区分每个样本是否可以归为第i类。

2-6-4. 归一化或取对数

逻辑回归中的梯度下降算法对特征的尺度敏感，如果特征具有不同的尺度，可能导致收敛速度变慢或者无法收敛。因此，为了保证梯度下降的效果，常常需要对特征进行归一化处理。另外，取对数操作可以将数据压缩到一个较小的范围内，有助于模型训练时的数值稳定性。

由于概率的乘积会因为很多原因不便使用（如容易出现数值下溢出），因此转换为对数的形式

2-6-5. 特征离散化效果提升：

1. 在工业界很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列 0/1 的离散特征。其优势有：

   • 离散化之后得到的稀疏向量，内积乘法运算速度更快，计算结果方便存储。

   • 离散化之后的特征对于异常数据具有很强的鲁棒性。如：销售额作为特征，当销售额在 [30,100) 之间时，为1，否则为 0。如果未离散化，则一个异常值 10000 会给模型造成很大的干扰。由于其数值较大，它对权重的学习影响较大。

   • 逻辑回归属于广义线性模型，表达能力受限，只能描述线性关系。特征离散化之后，相当于引入了非线性，提升模型的表达能力，增强拟合能力。假设某个连续特征 $j$ ，它离散化为 $M$ 个 0/1 特征 $j_{1}, j_{2}, \cdots, j_{M}$ 。则$w_{j} * x_{j} \rightarrow w_{j_{1}} * x_{j_{1}}^{\prime}+w_{j_{2}} * x_{j_{2}}^{\prime}+\cdots+w_{j_{M}} * x_{j_{M}}^{\prime}$ 。其中 $x_{j_{1}}^{\prime}, \cdots, x_{j_{\mu}}^{\prime}$ 是离散化之后的新的特征，它们的取值空间都是 ${0,1}$ 。上式右侧是一个分段线性映射，其表达能力更强。

   • 离散化之后可以进行特征交叉。假设有连续特征 $j$，离散化为 $M$ 个 0/1 特征；连续特征 $k$，离散化为 $N$ 个 0/1 特征，则分别进行离散化之后引入了 $M+N$ 个特征。假设离散化时，并不是独立进行离散化，而是特征 $M+N$ 联合进行离散化，则可以得到 $M\times N$ 个组合特征。这会进一步引入非线性，提高模型表达能力。

   • 离散化之后，模型会更稳定。如对销售额进行离散化，[30,100) 作为一个区间。当销售额在40左右浮动时，并不会影响它离散化后的特征的值。但是处于区间连接处的值要小心处理，另外如何划分区间也是需要仔细处理。

2. 特征离散化简化了逻辑回归模型，同时降低模型过拟合的风险。能够对抗过拟合的原因：经过特征离散化之后，模型不再拟合特征的具体值，而是拟合特征的某个概念。因此能够对抗数据的扰动，更具有鲁棒性。另外它使得模型要拟合的值大幅度降低，也降低了模型的复杂度。

2-6-6. 类别不平衡处理方法

• 对于类别不平衡问题，常用的有三种方法：

  • 基于再缩放策略进行决策，称之为阈值移动threshold-moving 。

  • 直接对训练集里的反类样本进行欠采样undersampling。

  • 直接对训练集里的正类样本进行过采样oversampling。

再缩放

1. 假设对样本 $\overrightarrow{\mathbf{x}}$ 进行分类时，预测为正类的概率为 p。常规的做法是将p 与一个阈值，比如 0.5 ， 进行比较。 如果 p>0.5 时，就判别该样本为正类。概率 p 刻画了样本为正类的可能性， 几率 $\frac{p}{1-p}$ 刻画了正类可能性与反类可能性的比值。

2. 当存在类别不平衡时，假设 $N^{+}$ 表示正类样本数目，$N^{-}$ 表示反类样本数目，则观测几率是 $\frac{N^{+}}{N^{-}}$。假设训练集是真实样本总体的无偏采样，因此可以用观测几率代替真实几率。于是只要分类器的预测几率高于观测几率就应该判断为正类。即如果 $\frac{p}{1-p}>\frac{N^{+}}{N^{-}}$ ， 则预测为正类。

3. 通常分类器都是基于概率值来进行预测的，因此需要对其预测值进行调整。在进行预测的时候，令：

   $$
   \frac{\overline{p}}{1-\overline{p}}=\frac{p}{1-p} \times \frac{N^{-}}{N^{+}}
   $$
   然后再将 $\overline{p}$ 跟阈值比较。这就是类别不平衡学习的一个基本策略：再缩放rescalling 。

4. 再缩放虽然简单，但是由于“训练集是真实样本总体的无偏采样”这个假设往往不成立，所以无法基于训练集观测几率来推断出真实几率。

欠采样（下采样）

1. 欠采样会去除一些反类使得正、反类数目接近。

2. 欠采样若随机抛弃反类，则可能丢失一些重要信息。常用方法是将反类划分成若干个集合供不同学习器使用，这样对每个学习器来看都是欠采样，但是全局来看并不会丢失重要信息。

过采样（上采样）

1. 过采样会增加一些正类使得正、反类数目接近。

2. 过采样不能简单的对原始正类进行重复采样，否则会导致严重的过拟合。

   通常在原始正类之间插值来生成额外的正类。

3. 常见的有以下过采样策略：

   • SMOTE方法：对于每个正类样本 $\overrightarrow{\mathbf{x}}{i}^{+}$ ，从它的 $k$ 近邻中随机选取一个样本点 $\hat{\mathbf{x}}{i}^{+}$ ，然后根据下式生成一个新的正类样本：$\overrightarrow{\mathbf{x}}{n e w}^{+}=\overrightarrow{\mathbf{x}}{i}^{+}+\left(\hat{\mathbf{x}}{i}^{+}-\overrightarrow{\mathbf{x}}{i}^{+}\right) \times \delta$ ，其中 $\delta \in[0,1]$ 是随机数。（插值方法）

• 该方法有两个问题：

  • 增加了正类样本之间重叠的可能性。

  • 生成了一些没有提供有益信息的样本。

2-6-7. L1和L2正则化作用、L1比L2更容易产生稀疏解的原因、L1正则化在存在线性相关的特征组中的特点

• L1正则化（Lasso）和L2正则化（Ridge）都是用于控制模型复杂度、防止过拟合的方法。
• L1正则化的作用是通过对模型的系数施加稀疏性惩罚，促使部分系数变为零，从而实现特征选择的效果。L2正则化则通过对模型的系数施加平方惩罚，倾向于让所有系数都趋近于零但不为零。L1正则化比L2正则化更容易产生稀疏解的原因是L1正则化的惩罚项具有角点，而L2正则化的惩罚项是圆形。在角点处，系数更容易变为零，从而实现特征的稀疏性。
• 在存在线性相关的一组特征中，L1正则化会倾向选择其中的一个特征，而将其他相关特征的系数变为零。这是因为L1正则化的惩罚项对于绝对值较大的系数更敏感，而对于相关特征中的系数，它们的绝对值相对较小，更容易被L1正则化压缩为零。

• 从解空间的形状来看：

  • L1正则项约束后的解空间是多边形，而L2正则项约束后的解空间是圆形。而多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。
  • 对于存在线性相关的一组特征，L1正则会使得部分参数为0

• 从函数叠加的观点：

权重衰减（L2正则化的作用）

作用：权重衰减（L2正则化）可以避免模型过拟合问题。
思考：L2正则化项有让w变小的效果，但是为什么w变小可以防止过拟合呢？
原理：（1）从模型的复杂度上解释：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合更好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。（2）从数学方面的解释：过拟合的时候，拟合函数的系数往往非常大，为什么？如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

2-6-8. 交叉熵作为损失函数、梯度下降优化方法的参数更新公式：

似然函数：
$$
L(w)=\prod\left[\pi\left(x_{i}\right)\right]^{y_{i}}\left[1-\pi\left(x_{i}\right)\right]^{1-y_{i}}
$$
对数似然函数：
$$
\begin{aligned} \ln L(w) &=\sum\left[y_{i} \ln \pi\left(x_{i}\right)+\left(1-y_{i}\right) \ln \left(1-\pi\left(x_{i}\right)\right)\right] \=& \sum\left[y_{i} \ln \frac{\pi\left(x_{i}\right)}{1-\pi\left(x_{i}\right)}+\ln \left(1-\pi\left(x_{i}\right)\right)\right] \ &=\sum\left[y_{i}\left(w \cdot x_{i}\right)-\ln \left(1+e^{w \cdot x_{i}}\right)\right] \end{aligned}
$$
损失函数：负对数似然函数
$$
J(W)=-\frac{1}{n} \ln L(w)
$$
使用梯度下降法求解逻辑回归参数估计

$$
\begin{aligned} J\left(w_{k}\right) &=-\frac{1}{N} \ln L\left(w_{k}\right) \Rightarrow-\ln L\left(w_{k}\right) \=-& \sum\left[y_{i}\left(w_{k} \cdot x_{i}\right)-\ln \left(1+e^{w_{k} \cdot x_{i}})\right]\right.\end{aligned}
$$

$$
\begin{aligned} g\left(w_{k}\right) &= -\frac{1}{N}\sum_i\left[x_{i} \cdot y_{i}-\frac{x_{i} \cdot e^{w_{k} \cdot x_{ik}}}{1+e^{w_{k} \cdot x_{i}}}\right] \ &=-\frac{1}{N}\sum_i x_{ik} \left[ y_{i}-\pi\left(w_{k}\cdot x_{i}\right)\right] \end{aligned}
$$

2-6-9. 训练函数代码示例

• 下面是一个简单的逻辑回归训练函数的代码示例，假设使用梯度下降作为优化方法和交叉熵作为损失函数：

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def train_logistic_regression(X, y, learning_rate=0.01, num_iterations=1000):
    num_samples, num_features = X.shape
    theta = np.zeros(num_features)  # 初始化参数为零向量

    for i in range(num_iterations):
        # 计算预测概率
        y_pred = sigmoid(np.dot(X, theta))

        # 计算损失和梯度
        loss = -np.mean(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred))
        gradient = np.dot(X.T, (y_pred - y)) / num_samples

        # 更新参数
        theta -= learning_rate * gradient

        # 打印损失
        if (i+1) % 100 == 0:
            print(f"Iteration {i+1}/{num_iterations}, Loss: {loss}")

    return theta

# 使用示例
X = np

2-7. FM模型

2-7-1. FM模型 v.s. 逻辑回归

• 优点：
  • FM模型可以处理高维稀疏数据，并且对特征之间的交互进行建模，能够更好地捕捉特征之间的非线性关系。
  • FM模型适用于特征较多的情况，并且在特征稀疏的情况下仍然能够有效工作。
  • FM模型相对于逻辑回归模型来说，更加灵活，可以处理更复杂的问题。
• 缺点：
  • FM模型的计算复杂度较高，随着特征数量的增加而增加，因此在大规模数据集上的训练和预测可能会比较慢。
  • FM模型对于特征之间的高阶交互项建模能力有限，无法捕捉更复杂的特征关系。
  • FM模型对于特征之间的线性关系建模能力较弱，适用性有一定限制。

2-7-2. FM计算复杂度

• FM（Factorization Machine）模型的计算复杂度可以分为两个部分：训练阶段和预测阶段。

  • 训练阶段的计算复杂度：在训练阶段，FM模型主要是通过梯度下降等优化算法来学习模型的参数。对于一个训练样本，假设特征的数量为n，因子的维度为k。
    • 线性部分的计算复杂度：对于线性部分，需要计算每个特征的一阶权重。因此，计算复杂度为O(n)。
    • 交互部分的计算复杂度：对于交互部分，需要计算每个特征交互的二阶权重。由于FM模型使用了因子分解，交互部分的计算复杂度可以通过因子维度k来表示。对于每个特征交互，需要进行k次乘法和k次加法操作。因此，计算复杂度为O(kn)。
  • 综上所述，FM模型在训练阶段的计算复杂度为O(n + kn)。

• 预测阶段的计算复杂度：在预测阶段，FM模型需要计算线性部分和交互部分的结果，并进行求和操作。

  • 线性部分的计算复杂度：与训练阶段相同，计算复杂度为O(n)。

  • 交互部分的计算复杂度：与训练阶段相同，计算复杂度为O(kn)。

• 综上所述，FM模型在预测阶段的计算复杂度为O(n + kn)。

• 需要注意的是，这里的计算复杂度是指在每个样本上的计算量，而对于整个数据集的计算复杂度则取决于样本数量和特征的平均数量。因此，FM模型的总体计算复杂度可以视为O(m * (n + kn))，其中m表示样本数量。在处理大规模数据集时，FM模型的计算复杂度可能会成为一个挑战，特别是当特征数量和因子维度较大时。

2-7-3. FFM v.s. FM

• 相同点：FFM（Field-aware Factorization Machine）模型和FM（Factorization Machine）模型都是用于处理特征交互的模型，并且都具有建模高阶特征交互的能力。
• 不同点：FFM模型在FM模型的基础上引入了字段信息。字段是指特征的一种分类，例如在广告推荐系统中，可以将特征按照广告主、广告位等字段进行分类。FFM模型考虑了不同字段之间的特征交互，使得模型能够更好地捕捉特征之间的相关性。与此相比，FM模型将所有特征都看作一个字段，无法区分不同字段之间的交互。

2-7-4. FM核心参数

• 因子维度（k）：因子维度决定了模型对于特征交互的建模能力，较大的因子维度可以更好地捕捉高阶特征交互，但会增加模型的计算复杂度。
• 正则化参数（lambda）：正则化参数控制模型的复杂度，过高的正则化参数会导致模型欠拟合，而过低的正则化参数会导致模型过拟合。
• 学习率（learning rate）：学习率决定了模型在每次参数更新时的步长，过高的学习率可能导致训练过程不稳定，而过低的学习率可能导致收敛速度过慢。
• 迭代次数（num_iterations）：迭代次数决定了模型的训练轮数，过少的迭代次数可能导致模型未能充分学习，而过多的迭代次数可能会增加计算开销。

2-7-5. 神经网络的视角看FM

​ 从神经网络的视角看，FM模型可以看作是一个浅层的神经网络。FM模型通过将输入特征进行隐式的交叉，得到特征交叉的隐含向量表示，并将这些隐含向量与输入特征的线性组合相加，最终输出一个预测结果。

​ 在FM模型中，特征交叉的隐含向量可以看作是学习到的特征表示，类似于神经网络中隐藏层的神经元。这些隐含向量捕捉了特征之间的交互关系，类似于神经网络中神经元之间的连接权重。

​ FM模型的特点是它可以处理高维稀疏数据，并且能够对特征之间的交互进行建模。这种能力与神经网络中的全连接层相似，全连接层可以处理任意特征之间的交互，但需要大量的参数和计算资源。相比之下，FM模型通过使用因子分解的方法，以较少的参数和计算量来实现特征交互建模的能力。

​ 因此，可以将FM模型看作是一种浅层、高效的神经网络模型，适用于处理高维稀疏数据和特征交互建模的任务。

2-8. 决策树

2-8-1. 建树过程

1. 选择根节点：从数据集中选择一个特征作为根节点，可以根据不同的准则进行选择，如信息增益、基尼指数等。
2. 分裂节点：根据选择的特征，将数据集分成不同的子集，每个子集对应一个分支。
3. 递归分裂：对每个子集重复上述步骤，选择特征并进行分裂，直到满足终止条件，如达到预定的树深度或子集中的样本数小于某个阈值。
4. 构建叶节点：当满足终止条件时，将子集划分为叶节点，并为叶节点分配标签或类别。

2-8-2. 熵

熵（entropy）是表示随机变量不确定性的度量， $X$ 是一个取有限个值的离散随机变量，其概率分布为
$$
P(X = x_i) = p_i, \ i=1,2,\cdots,n
$$
则随机变量 $X$ 的熵定义为
$$
H(X) = -\sum_{i=1}^{n} p_i {\rm log_2 } \ p_i
$$
熵越大，随机变量的不确定性就越大。$H(X)$表示随机变量$X$的熵，$p(x)$表示X取某个值x的概率。熵的值越大，表示随机变量的不确定性越高。而熵其实表示的是一个系统的平均信息量。自信息量是用来描述某一条信息的大小

$$
I = - {\rm log} \ p_i
$$

通常以2为底，单位是bit；含义是用多少位二进制可以表示衡量该信息的大小。而通常我们衡量整个系统的信息量，系统存在多个事件 $X={x_1,\cdots,x_n}$ ，每个事件的概率分布$P={p_1,\cdots,p_n}$ ，熵是整个系统的平均信息量 。

从数学原理上解释，熵公式可以作为信息不确定性的度量，是因为它满足以下性质：

• 当所有可能的取值的概率相等时，熵达到最大值，表示不确定性最高。
• 当某个取值的概率接近于1，而其他取值的概率接近于0时，熵接近于0，表示不确定性最低，即确定性最高。

2-8-3. 联合熵、条件熵、KL散度、信息增益、信息增益比、gini系数

• 联合熵（Joint Entropy）：指两个随机变量联合分布的熵，用于度量两个变量的不确定性。将一维随机变量分布推广到多维随机变量分布
  $$
  H(X,Y) = -\sum\limits_{x,y} p(x,y)\ {\rm log}\ p(x,y)
  $$

• 条件熵（Conditional Entropy）：指在给定一个随机变量的条件下，另一个随机变量的不确定性，用于度量一个变量在另一个变量已知的情况下的不确定性。某个特征A对于数据集D的经验条件熵 $H(D|A)$ 为
  $$
  H(D|A) = - \sum_{i=1}^{n} \frac{|D_i|}{|D|} H(D_i) \ = - \sum_{i=1}^{n} \frac{|D_i|}{|D|} \lgroup \sum_{k=1}^{K} \frac{|D_{ik}|}{|D_i|} {\rm log } \frac{|D_{ik}|}{|D_i|} \rgroup
  $$

• 信息增益（Information Gain）：用于衡量在决策树算法中选择一个特征进行分裂后，分类结果的纯度提高了多少，是熵的减少量。 $g(D,A)$ 定义为数据集D的经验熵 $H(D)$ 与特征A给定条件下D的经验条件熵 $H(D|A)$ 的差
  $$
  g(D,A) = H(D) - H(D|A)
  $$

• 信息增益比（Gain Ratio）：信息增益除以划分信息，用于解决信息增益对可取值数目较多的特征偏好的问题。特征A对于数据集D 的信息增益比定义为:
  $$
  g_R(D|A) = \frac{g(D|A)}{H_A(D)}
  $$
  其中 :
  $$
  H_A{(D)} = - \sum_{i=1}^{n} \frac{|D_i|}{|D|} {\rm log } \frac{|D_i|}{|D|}
  $$
  为数据集D关于A的取值熵；n为特征A在D上的取值数目；

• Gini系数：描述数据的不确定性。数据集D的Gini系数为

$$
{\rm Gini}(D) = 1 - \sum_{k=1}^{K
}(\frac{|C_k|}{|D|})^2
$$

​ 其中 $C_k$是 D中第k类的样本子集，K是类的个数。例如二分类问题，K=2。基尼系数越大，样本集合的不确定性也就越大，这一点与熵相似。基尼系数Gini(D,A)表示经A=a分割后集合D的不确定性。

• 交叉熵：刻画两个概率分布之间的距离，通过q来表示p的交叉熵为；一般p(x)为真实分布，q(x)为预测分布。交叉熵不对称。交叉熵越小，概率分布越接近

$$
H(p,q) = - \sum\limits_{x} p(x) {\rm log } \ q(x)
$$

• KL散度/相对熵，KL散度（Kullback-Leibler Divergence）：度量两个概率分布之间的差异或相似性，用于衡量一个分布相对于另一个分布的不确定性。：

$$
D_{K L}(p | q)=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right)
$$

n表示事件可能发生的情况总数，KL散度的值越小表示两个分布越接近。
$$
D_{KL}(p||q) = H(p,q) - H(p)
$$

机器学习中，我们常常使用KL散度来评估predict和label之间的差别，但是由于KL散度的后半部分是一个常量，所以我们常常将前半部分的交叉熵作为损失函数，其实二者是一样的。

2-8-4. ID3、C4.5、CART：

• ID3：使用信息增益作为特征选择准则，对离散特征进行处理。信息增益 $g(D,A)$ 定义为数据集D的经验熵 $H(D)$ 与特征A给定条件下D的经验条件熵 $H(D|A)$ 的差
  $$
  g(D,A) = H(D) - H(D|A)
  $$
  选择 $g(D,A)$ 最大的特征，所有样本根据此特征，划分到不同的节点上。在经验熵不为0的节点中继续生长。ID3算法只有树的生成，容易产生过拟合。

• C4.5：类似于ID3，但使用信息增益比作为特征选择准则，可以处理离散特征和连续特征，并且支持缺失值处理。因为信息增益对取值数目多的属性有所偏好，为了减少这种偏好带来的影响，使用信息增益比来选择最优划分属性。

• CART（Classification and Regression Trees）：可以处理分类和回归问题，使用基尼指数作为特征选择准则，对离散特征和连续特征进行处理。基尼系数Gini（D）用来表示集合D的不确定性。CART在每一次迭代中选择划分后基尼指数最小的特征及其对应的切分点进行分类。CART是一颗二叉树，每次将数据按特征A的区分分成两份，分别进入左右子树。

• Comparison

不同点	ID3	C4.5	CART
原则	信息增益最大	信息增益比最大	划分后集合基尼指数最小
用途	分类	分类	分类、回归
输入取值	离散	离散、连续	离散、连续
树结构	多叉树	多叉树	二叉树
	特征在层级间不复用	特征在层级间不复用	每个特征可被重复利用
	对样本特征缺失值敏感

2-8-5. 防止过拟合

• 减枝方法

  • 前剪枝：在建树过程中，在决策树的节点分裂之前进行判断，如果继续分裂不能显著提高模型性能，就停止分裂并将当前节点标记为叶节点。这样可以避免过度拟合训练数据，但可能会导致欠拟合。

  • 后剪枝：在建树完成后，对决策树进行剪枝操作。通过递归地从底部向上剪枝，将一些子树替换为叶节点。剪枝过程使用验证集来评估剪枝后的模型性能，如果剪枝后模型性能没有显著下降，则进行剪枝操作。这样可以在一定程度上减小过拟合。

• 剪枝的条件通常包括：

  • 树的深度达到预定的最大深度。

  • 叶节点中的样本数小于某个阈值。

  • 分裂后的子节点的性能不能显著提升。

剪枝过程的具体实现会根据不同的算法和实际情况而有所差异。

2-9. 随机森林(RF)

2-9-1. RF原理和思想

​ RF由多个决策树组成，这些决策树被称为基分类器或弱学习器。每个决策树都是通过对训练集进行有放回抽样（Bootstrap）得到的不同样本集进行训练，这样可以保证每个决策树都是基于不同的数据子集进行训练。
​ 决策树的建立过程中，每次划分特征的选择是在随机选择的一部分特征集合中进行，以增加随机性。最终的分类结果是由所有决策树的投票或平均得到。RF的思想在于通过随机化和集成学习的方式，减小了单棵决策树的过拟合风险，提高了模型的泛化能力。

2-9-2. RF处理缺失值处理

• 缺失值的处理方法主要是通过在决策树的节点分裂过程中，将缺失值样本按照概率分配给不同的子节点。在决策树的训练过程中，对于缺失值样本，可以根据已有特征的取值和缺失值样本在该特征上其他样本的分布情况，计算出一个概率分布，然后根据这个概率分布将缺失值样本分配给不同的子节点。

2-9-3. 特征重要度衡量

• RF衡量特征重要度的方法主要是通过计算特征在决策树中的分裂准则的贡献度。一种常用的度量方法是基于Gini指数或基于信息增益的方法。在RF中，对于每个决策树，可以计算出特征在每个节点上的分裂准则的减少量，然后将所有决策树中相应节点的减少量进行平均或加权平均，得到特征的重要度。

2-9-4. RF中的随机

• RF中的“随机”，体现在以下几个方面：
  • 随机抽样：通过有放回抽样（Bootstrap）得到不同的训练数据子集，用于训练每棵决策树。
  • 随机特征选择：在决策树的节点分裂过程中，随机选择一部分特征进行划分。
  • 随机子空间：在决策树的节点分裂过程中，对于每棵决策树，随机选择特征的子集用于训练。
  • 这些随机性的引入可以增加模型的多样性，减小过拟合的风险。

2-9-5. RF的优缺点

• 优点
  • 具有较好的泛化能力和鲁棒性，能够处理高维数据和大规模数据集。
  • 在训练过程中可以评估特征的重要度，有助于特征选择和特征工程。
  • 容易并行化处理，适合分布式计算。
• RF的局限性包括：
  • 对于高维稀疏数据，可能效果不如其他方法。
  • 对于含有大量噪声特征的数据，RF可能受到影响。
  • RF的结果难以解释，不如单棵决策树直观。

2-9-6. 弱分类器的组合

• 多个弱分类器组合效果比单个好的原因在于集成学习的思想。弱分类器是指分类效果略好于随机猜测的分类器，它们可能在某些情况下不能很好地进行分类。然而，通过将多个弱分类器组合起来，可以获得更强大的分类器，这被称为集成学习。集成学习通过对多个弱分类器的预测进行组合，可以减少模型的偏差和方差，从而提高整体的预测性能。当每个弱分类器都有一定的分类误差时，通过集成它们的预测，可以减小误差的影响，从而得到更准确的预测结果。
• 弱分类器的组合可以通过多种方式实现，其中两种常见的方法是投票（Voting）和平均（Averaging）。在投票方法中，每个弱分类器对样本进行预测，最终的预测结果是根据投票多少来确定的。在平均方法中，每个弱分类器对样本进行预测，最终的预测结果是这些预测值的平均值。多个弱分类器组合效果比单个好的原因是，它们能够相互弥补各自的缺点。不同的弱分类器可能在不同的样本或特征子集上表现较好，通过集成它们的预测，可以综合利用它们的优势。此外，通过集成多个弱分类器，可以减少模型的方差，提高模型的鲁棒性和泛化能力。

2-9-7. Bagging

• Bagging（自举汇聚法）是一种集成学习方法，其思想是通过自助采样（Bootstrap）和多个基分类器的平均来降低方差。Bagging的主要思想是通过有放回地从原始训练集中进行有放回抽样，形成多个与原始训练集大小相等的自助样本集，然后使用这些自助样本集分别训练多个基分类器。最后，通过对多个基分类器的预测结果进行平均或投票，得到最终的集成预测结果。
• Bagging主要用于降低方差，通过引入随机性和多样性，减少模型对训练集的过拟合程度。每个自助样本集都是从原始训练集中有放回地抽样得到的，这导致每个自助样本集都略微有所不同，从而使每个基分类器训练的数据集有所不同，进而产生多样性。通过对多个基分类器的预测结果进行平均，可以减小预测结果的方差，提高整体的预测性能。
• Bagging在降低方差的同时，通常会保持偏差不变或稍微增加。这是因为Bagging会引入更多的随机性和多样性，可能导致一些基分类器的错误相互抵消，但也可能导致一些基分类器的错误相互放大。然而，通过集成多个基分类器的预测结果，整体上可以获得更好的预测性能。

2-9-8. RF基分类模型选择

• RF的基分类模型通常使用决策树，而不是线性模型或KNN。这是因为RF的随机性和集成学习的思想与决策树相结合，形成了RF独特的特点和优势。决策树具有以下特点，使其适合用作RF的基分类模型：

  • 非线性关系建模能力：决策树可以自由地建模非线性关系，因为它们通过分裂节点来适应数据的非线性特征。这使得决策树能够处理各种类型的数据，包括离散特征和连续特征。
  • 鲁棒性：决策树对异常值和噪声数据具有较好的鲁棒性。由于每个决策树都是基于随机抽样的训练数据构建的，它们对于数据中的异常值和噪声相对不敏感。因此，RF在面对含有噪声的数据集时表现良好。
  • 特征重要度评估：决策树可以提供对特征重要度的评估。在RF中，通过对多个决策树中的特征重要度进行平均，可以得到整体的特征重要度排序。这有助于特征选择和特征工程，帮助识别对于预测任务最具有预测能力的特征。
  • 可解释性：相比其他复杂的模型，决策树具有更高的可解释性。决策树的每个节点和分裂规则都可以直观地解释为特征的判断条件，使得RF的预测结果更易于理解和解释。

• 尽管决策树在许多方面表现出色，但也有一些局限性，例如：

  • 容易过拟合：单个决策树容易受到训练数据的细微变化而产生过拟合。然而，通过RF的集成学习方法，可以减少过拟合的风险。
  • 高方差：单个决策树的预测结果可能具有较高的方差，尤其是在处理高维数据时。通过RF的集成方法，可以降低方差并提高模型的稳定性和泛化能力。
  • 尽管RF的基分类模型通常使用决策树，但在某些情况下，也可以尝试将基分类模型改为线性模型或K最近邻（KNN）等其他模型。这样的组合被称为随机权重线性模型（Random Weighted Linear Model）或随机权重KNN（Random Weighted KNN）。通过引入随机性和集成学习的思想，这些方法也可以提供一些优势，如降低方差和提高泛化能力。

• 然而，需要注意的是，这些改变可能会影响RF的性能和特性。决策树之所以成为RF的流行选择，是因为它们与RF的随机性和集成学习思想相匹配，并且在许多应用中表现出色。选择不同的基分类模型可能需要进行更多的实验和评估，以确定是否能够获得与决策树相当或更好的性能。

2-10. GBDT

2-10-1. 梯度提升 v.s. 梯度下降

两个不同的概念。梯度提升是一种集成学习算法，通过迭代地训练弱学习器来构建一个强学习器，每次迭代都试图拟合前一次迭代的残差。而梯度下降是一种优化算法，用于最小化目标函数，通过迭代地更新模型参数来找到目标函数的最优解。梯度提升使用梯度下降的思想来训练每个弱学习器，但两者的应用场景和目标不同。

2-10-2. Boosting v.s. Bagging

Boosting和Bagging都是集成学习的方法。Boosting是一种迭代的集成学习方法，通过训练一系列的弱学习器，每个弱学习器都尝试修正前一个学习器的错误，最终将这些弱学习器进行加权结合得到最终的预测结果。而Bagging是一种并行的集成学习方法，通过随机有放回地从训练集中抽取样本来构建多个弱学习器，最终通过投票或平均等方式进行集成。它们的异同在于训练方式和集成策略的不同。

	Bagging	Boosting
降低	方差	偏差
训练	各个弱分类器可独立训练	弱分类器需要依次生成
典型方法	随机森林	Adaboost，GBDT，XGBoost

2-10-3. GBDT训练过程

1. 初始化模型：将目标变量的均值作为初始预测值，作为第一个弱学习器的预测结果。
2. 迭代训练：对于每一轮迭代，计算当前模型的残差（目标值减去当前模型的预测值），将残差作为新的目标变量，训练一个新的弱学习器来拟合残差。
3. 更新模型：将新的弱学习器加入到模型中，并更新模型的预测结果，将当前模型的预测值与新的弱学习器的预测结果按一定比例相加，得到更新后的模型预测值。
4. 重复步骤2和步骤3，直到达到预定的迭代次数或满足停止条件。

2-10-4. GBDT训练效率提升

• 特征并行：在每个迭代中，可以并行计算每个特征的梯度和Hessian矩阵的统计量，以加速特征选择过程。
• 数据并行：如果数据量较大，可以将数据划分为多个子集，每个子集独立地训练一个弱学习器，最后进行模型融合。

决策树内部局部并行。

2-10-5. GBDT优缺点

• 优点

  • 预测阶段计算速度快，树与树之间可并行化计算
  • 在分布稠密的数据集上，泛化能力和表达能力都很好
  • 采用决策树作为弱分类器使得GBDT模型具有较好的可解释性和鲁棒性，能够自动发现特征间的高阶关系，并且不需要对数据进行特殊的预处理如归一化等

• 缺点

  • GBDT在高维稀疏的数据集上，表现不如支持向量机或者神经网络
  • GBDT在处理文本分类特征问题上，优势不如在处理数值特征时明显
  • 训练过程需要串行训练，只能在决策树内采用一些局部并行手段提高训练速度

2-10-6. GBDT异常值敏感问题

在训练过程中，每个弱学习器都试图拟合前一轮弱学习器的残差，如果某个样本的残差较大，它可能会对后续弱学习器的拟合产生较大的影响，导致模型对异常值过于敏感。

GDBT对异常值敏感。对于回归类的问题，如果采用平方损失函数。当出现异常值时，后续模型会对异常值关注过多。

2-10-7. 防止GBDT过拟合

1. 在工程应用中，通常利用下列公式来更新模型： $f_{m}(\overrightarrow{\mathbf{x}})=f_{m-1}(\overrightarrow{\mathbf{x}})+\nu h_{m}\left(\overrightarrow{\mathbf{x}} ; \Theta_{m}\right), \quad 0<\nu \leq 1$。

   其中 $\nu$ 称作学习率。学习率是正则化的一部分，它可以降低模型更新的速度（需要更多的迭代）。

   • 经验表明：一个小的学习率 ($\nu<0.1$) 可以显著提高模型的泛化能力（相比较于$\nu=1$ ) 。
   • 如果学习率较大会导致预测性能出现较大波动。

2. Freidman 从bagging 策略受到启发，采用随机梯度提升来修改了原始的梯度提升树算法。

   • 每一轮迭代中，新的决策树拟合的是原始训练集的一个子集（而并不是原始训练集）的残差。

     这个子集是通过对原始训练集的无放回随机采样而来。

   • 子集的占比 $f$ 是一个超参数，并且在每轮迭代中保持不变。

     • 如果 $f=1$ ，则与原始的梯度提升树算法相同。
     • 较小的$f$ 会引入随机性，有助于改善过拟合，因此可以视作一定程度上的正则化。
     • 工程经验表明， $0.5 \leq f \leq 0.8$会带来一个较好的结果。

   • 这种方法除了改善过拟合之外，另一个好处是：未被采样的另一部分子集可以用来计算包外估计误差。因此可以避免额外给出一个独立的验证集。

3. 梯度提升树会限制每棵树的叶子结点包含的样本数量至少包含 $m$ 个样本，其中 $m$为超参数。在训练过程中，一旦划分结点会导致子结点的样本数少于 $m$，则终止划分。这也是一种正则化策略，它会改善叶结点的预测方差。

• 此外：
  • 正则化：通过在目标函数中引入正则化项（如L1正则化、L2正则化），限制模型的复杂度，防止过拟合。
  • 提前停止：监控模型在验证集上的性能指标，当性能不再提升时，提前停止训练，避免过拟合。
  • 降低学习率：减小每个弱学习器的权重更新步长，可以使模型收敛得更慢，从而减小过拟合的风险。

2-10-8. 对GBDT影响大的参数

减小步长需要对应增加最大迭代次数

1. n_estimators: 也就是弱学习器的最大迭代次数，或者说最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合，一般选择一个适中的数值。默认是100。在实际调参的过程中，我们常常将n_estimators和下面介绍的参数learning_rate一起考虑。

2. learning_rate: 即每个弱学习器的权重缩减系数νν，也称作步长，在原理篇的正则化章节我们也讲到了，加上了正则化项

3. subsample: 即我们在原理篇的正则化章节讲到的子采样，取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间，默认是1.0，即不使用子采样。

2-11. k-means

• kmean的总体特点

  • 基于划分的聚类方法

  • 类别k事先指定

  • 以欧式距离平方表示样本之间的距离

  • 以中心或样本的均值表示类别

  • 以样本和其所属类的中心之间的距离总和为最优化的目标函数

  • 得到的类别是平坦的、非层次化的

  • 算法是迭代算法，不能保证全局最优

2-11-1. kmeans建模过程

• kmeans聚类是基于样本集合划分的聚类算法
  1. 首先随机选择k个样本点作为初始聚类中心
  2. 计算每个样本到类中心的距离，将样本逐个指派到与其最近的类中，得到一个聚类结果
  3. 更新每个类的样本的均值，作为新的中心
  4. 重复以上步骤，直到划分不再改变，收敛为止

kmeans的算法复杂度是$O(mnk)$，其中m是样本位数，n是样本个数，k是类别个数。比层次聚类复杂度低。

2-11-2. kmeans损失函数

样本与所属类的中心之间的距离的总和为损失函数
$$
W(C) = \sum_{l=1}^k \sum_{C(i)=l} {||x_i - \overline{x}_l||}
$$
其中 $\overline{x}_l$ 是第 $l$ 个类的均值或中心。相似的样本被聚到同类时，损失函数值最小。但是这是一个组合优化问题，n个样本分到k个类，可能的分法数目是指数级的，NP难问题。采样迭代的方法求解。

2-11-3. 如何选择初始类族的中心点

• 初始类中心点的选择: 可以用层次聚类对样本进行聚类，得到k个类时停止。然后从每个类中选取一个与中心距离最近的点。

• 类别数k的选择: k值需要预先指定，而在实际应用中最优的k值是不知道的。解决这个问题的一个方法是尝试用不同的k值聚类，检验各自得到聚类结果的质量，推测最优的k值

一般地，类别数变小时，平均直径会增加；类别数变大超过某个值后，平均直径会不变；而这个值是最优的k值。实验时可以采用二分查找，快速找到最优的k值。

2-11-4. kmeans效率

• kmeans时间复杂度 $O(nkt)$ n，k，t分别为样本数，聚类中心数，迭代轮次
  • 我们可以使用kd树以及ball 树（数据结构）来提高k-means算法的效率。（KNN计算的优化）
  • 并行计算

• 使用KD树等数据结构来加速最近邻搜索。
• 利用并行计算或分布式计算来加速计算过程。
• 对于大规模数据集，可以使用Mini-Batch K-Means算法来减少计算量。

2-11-5. 常用的距离衡量、适用什么类型问题

• 欧氏距离：适用于连续型数据的聚类问题。
• 曼哈顿距离：适用于连续型数据的聚类问题，尤其对于具有较多离群值的数据更鲁棒。
• 闵可夫斯基距离：是欧氏距离和曼哈顿距离的一种推广形式，适用于连续型数据的聚类问题。
• 马哈拉诺比斯距离：适用于考虑各个特征之间相关性的聚类问题。

2-11-6. Kmeans对异常值敏感

k-means算法是基于距离的聚类算法，异常值会对样本点与类族中心点之间的距离产生较大影响，从而可能导致聚类结果的偏差。敏感，因为需要计算距离，使用传统的欧式距离度量方式。所以需要预处理离群点、数据归一化。

2-11-7. 评估聚类效果

知乎：https://zhuanlan.zhihu.com/p/53840697

2-11-8. 超参数类个数k

（1）手肘法

尝试不同的K值，并将不同K值所对应的损失函数化成折线，横轴为K的取值，纵轴为误差平方和所定义的损失函数。K值越大，距离和越小。当K=K’时，存在一个拐点，像人的肘部。当 $K\in(1,K’)$，曲线急速下降；当 $K>K’$，曲线趋于平稳。手肘法认为拐点就是K的最佳值。

（2）Gap Statistic

手肘法是一个经验方法，缺点是不够自动化。Gap Statistic方法的优点是，不需要肉眼判断，只需要找到最大Gap statistic对应的K即可。因此该方法适用于批量化作业。
$$
{\rm Gap}(K) = E({\rm log}D_k) - {\rm log}D_k
$$
当分为K簇时，对应的损失函数记为 $D_k$，$E({\rm log}D_k)$是 ${\rm log}D_k$ 的期望，通过蒙特卡洛模拟产生。$\text{Gap}(K) $ 的物理含义是随机样本的损失与实际样本的损失之差。当$\text{Gap}(K) $取最大时，是样本的损失应该相对较小。

2-11-9. Kmeans优缺点、改进的模型

• 优点

  • 对于大数据集，kmeans聚类算法相对是可伸缩和高效的，它的计算复杂度是$O(NKt)$ 接近线性，其中N是样本数，K是聚类的簇数，t是迭代的轮数。
  • 尽管算法经常以局部最优解结束，但一般情况下达到的局部最优已经可以满足聚类的需求。

• 缺点

  • 受初值和离群点的影响，每次的结果不稳定
  • 结果通常不是全局最优而是局部最优解
  • 无法很好地解决数据簇分布差别比较大的情况（比如一类是另一类样本数量的100倍）
  • 不太适用于离散分类
  • K值需要人工预先确定，且该值和真实的数据分布未必吻合【最大缺点】
  • 样本点只能被划分到单一的类中

• 如何对Kmeans进行调优

  • 数据归一化和离群点处理: Kmeans聚类本质上是一种基于欧式距离度量的数据划分方法，均值和方差大的维度对聚类结果产生决定性影响。未做归一化无法直接参与计算；离群点或少量噪声会对均值产生较大影响，导致中心偏移。
  • 合理选择K值: 手肘法、Gap Statistic（不需要肉眼判断，只需要找到最大Gap statistic对应的K）

• 采用核函数: 核聚类。通过非线性映射，将输入空间中的数据点映射到高维的特征空间中，并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率，从而在经典的聚类算法失效的情况下，通过引入核函数可以达到更为准确的聚类效果

• 改进的模型

  • kmeans++ （对初始值选择的改进）: 原始的kmeans算法最开始随机选取数据集中K个点作为聚类中心，而kmeans++按照以下思想选取k个聚类中心：假设已经选取了n个初始聚类中心（0<n<k），则在选取第n+1个聚类中心时，距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。在选取第一个聚类中心时同样通过随机的方法。这符合我们的直觉：聚类中心互相离得越远越好。后续步骤与kmeans一致。
  • ISODATA（K值不确定时）: ISODATA全称是 迭代自组织数据分析法。在kmeans算法中，聚类个数K值需要预先人为确定，并且在整个算法过程中无法更改。当遇到高维度、海量数据时，难以准确估计出K的大小。ISODATA的思想是：当属于某个类别的样本数过少时，把该类别去除（合并操作）；当属于某个类别的样本数过多、分散程度大时，把该类别分为两个子类别（分裂操作）。缺点是需要制定的参数比较多，4个：预期聚类中心数目 $K_0$、每个类所要求的最少样本数目 $N_{min}$、最大方差 $\sigma$ 、两个聚类中心之间所允许最小距离 $D_{min}$。
  • 模糊C均值，高斯混合模型: 样本不划分到单一的类中，即软聚类。高斯混合模型：假设不同簇中的样本各自服从不同的高斯分布，由此得到的聚类算法称为高斯混合模型。在该假设下，每个单独的分模型都是标准高斯模型，其均值 $u_i$ 和方差 $\Sigma_i$ 是待估计的参数。瓷王每个分模型还都有一个参数 $\pi_i$，可以理解为权重或者生成数据的概率。$p(x)=\sum_{i=1}^{K}\pi_iN(x|u_i,\Sigma_i)$，高斯混合模型是一个生成式模型。相比Kmeans的优点：可以给出一个样本属于某类的概率是多少；不仅仅可以用于聚类，还可以用于概率密度的估计；并且可以用于生成新的样本点。

2-11-10. kmeans算法的收敛性

• kmeans聚类属于启发式方法，不能保证收敛到全局最优，初始中心的选择会直接影响聚类结果。
• 类中心在聚类过程中会发生移动，但是往往不会移动太大，因为在每一步，样本被分到与其最近的中心的类中。

2-11-11. 其他聚类算法、原理

• 层次聚类（hierarchical clustering）假设类别之间存在层次结构，分为聚合（自下而上）和分裂（自上而下）两种方法。聚合法开始讲每个样本各自分到一个类；之后将相邻最近的两类合并（根据类间距离最小合并规则），建立一个新的类，重复此操作直到满足停止条件（类的个数达到阈值/类的直径超过阈值）；得到层次化的分类。分裂法开始讲所有样本分到一个类；之后将已有类中相距最远的样本分到两个新的类，重复此操作直到满足停止条件；得到层次化的分类。层次聚类算法复杂度：$O(n^3m)$ 其中n是样本个数，m是样本维数。
• k-means聚类是基于中心的聚类方法，通过迭代，将样本分到k个类别中，使得每个样本与其所属类的中心或均值最近；得到k个平坦的、非层次化的类别。
• 基于密度的方法DBSCAN
• 谱聚类

kmeans初始化从数据中随机挑k个点

• 不可以；如果是用随机值，可能某个簇在第一轮就没有任何节点，无法继续计算

2-12. PCA降维

2-12-1. PCA作用

• 对数据进行降维的目的是减少特征的数量，从而简化数据集并提取最具信息量的特征。降维可以解决以下问题：

  • 维数灾难：随着特征数量的增加，数据变得稀疏，计算和存储成本增加，模型复杂度增加，容易出现过拟合等问题。降维可以减少维数灾难的影响。

  • 特征选择：某些特征可能对于建模和预测任务没有贡献，甚至可能引入噪声。降维可以帮助选择最相关的特征，提高模型性能和解释能力。

  • 数据可视化：降维可以将高维数据映射到低维空间，方便可视化和理解数据的结构和模式。

高维（多变量）数据，很难观察变量的样本区分能力，也很难观察样本之间的关系。降维是将样本集合中的样本从高维空间转换到低维空间。假设样本原本存在于低维空间，或近似存在与低维空间，通过降维则可以更好地表示样本数据的结构，即更好地表示样本之间的关系。降维有线性降维和非线性降维。

2-12-2. 维度灾难

维度灾难是指在高维空间中，数据的密度和距离变得非常稀疏，导致数据分布的不均匀性增加。这会对数据分析和建模带来挑战，因为在高维空间中，样本之间的距离和相似度难以准确度量，同时计算和存储高维数据的困难度也增加。特征数量超过一定值的时候，分类器的效果反而下降。原因：特征数过多，过拟合。

2-12-3. PCA思想

通过线性变换将原始特征空间映射到新的特征空间，使得新特征之间具有最大的方差，并且特征之间互相独立。这样可以实现数据的降维，同时保留了数据中最具信息量的特征。

变量之间可能存在相关性，以致增加了分析的难度。考虑用少数不相关的变量来替代相关的变量，用来表示数据，并且要求能保留数据中的大部分信息。PCA利用正交变换把线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，线性无关的变量称为主成分。PCA属于降维方法。

2-12-4. 主成分

主成分是指在PCA中得到的新特征空间中的特征向量。每个主成分都是原始特征的线性组合，其系数表示了原始特征对该主成分的贡献程度。主成分按照方差从大到小排列，第一主成分具有最大的方差，第二主成分具有次大的方差，依此类推。

2-12-5. 目标函数提取主成分

PCA的目标函数是最大化投影后数据的方差。通过选择投影方向，使得投影后数据的方差最大化，即表示保留了数据中最多的信息。这可以通过计算协方差矩阵的特征向量来实现，特征向量对应的特征值表示了数据在对应特征向量方向上的方差大小。

2-12-6. PCA局限性

• PCA是一种无监督降维方法，它只考虑数据的方差，可能无法充分挖掘类别间的差异。
• PCA假设数据在低维空间中是线性可分的，对于非线性关系的数据，效果可能不佳。
• PCA对异常值敏感，异常值可能会对主成分的计算产生较大影响。

• 无法进行非线性降维，通过核映射对PCA进行扩展得到核主成分分析（KPCA）。通过流形映射的降维方法，比如等距映射、局部线性嵌入（LLE）、拉普拉斯特征映射等。

• 无监督的，算法没有考虑数据的标签，只是把把元数据映射到方差比较大的方向。有监督的降维方法：线性判别分析 LDA。

2-12-7. 线性判别 v.s. 主成分分析

​ PCA选择的是投影后数据方差最大的方向。由于PCA是无监督的，因此假设方差越大，信息量越多，用主成分来表示原始数据可以去除冗余的维度，达到降维。

​ LDA选择的是投影后类内方差最小，类间方差最大的方向。其用到了类别标签信息，为了找到数据中具有判别性的维度，使得原始数据在这些方向投影后，不同类别尽可能区分开。

3. 深度学习

3-1. DNN

3-1-1. 神经网络定义

是一种模拟人脑神经系统的计算模型，由多个神经元（或称为节点）组成的网络。每个神经元接收来自上一层神经元的输入，并通过权重和偏置进行加权求和，并将结果输入到激活函数中进行非线性变换。这个过程在网络的前向传播中进行。反向传播是用于训练神经网络的一种方法，通过计算损失函数对网络参数的偏导数，从输出层向输入层逐层更新参数，以减小预测值和真实值之间的误差。（反向传播：偏导数，链式法则就OK）

3-1-2. Dropout

Dropout是一种正则化技术，用于减少神经网络的过拟合。在训练过程中，Dropout会随机地将一部分神经元的输出置为零，这样可以强制网络在不同的子集上进行训练，从而减少神经元之间的依赖关系。具体来说，Dropout会以一定的概率（通常为0.5）将神经元的输出置为零，然后通过缩放剩余输出，保持总体输出的期望不变。这样可以使得网络更加鲁棒，避免过拟合。

在神经网络前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征。

3-1-3. 梯度消失和梯度膨胀

梯度消失和梯度膨胀是在深度神经网络中经常遇到的问题。梯度消失指的是在反向传播过程中，梯度逐渐变小，导致更新较浅层的网络参数时梯度几乎为零，使得其学习能力变弱。梯度膨胀则是梯度逐渐变大，导致更新深层网络参数时梯度过大，使得网络参数发生剧烈的变化。这些问题的根本原因是深层网络中的链式导数求解过程中的乘法操作，导致梯度在传播过程中指数级地衰减或增长。

为缓解梯度消失的问题，可以使用激活函数的选择，如ReLU激活函数可以有效地缓解梯度消失。另外，批归一化（Batch Normalization）也可以帮助缓解梯度消失的问题，通过对每一层的输入进行归一化，使得激活值落在更合适的范围内。

对于梯度膨胀的问题，可以使用梯度裁剪（Gradient Clipping）方法，限制梯度的大小，防止其变得过大。此外，使用一些特殊的权重初始化方法，如Xavier或He初始化，也可以一定程度上缓解梯度膨胀问题。

注：任何网络都有可能发生梯度弥散或者梯度爆炸，这是深度学习的基本性质决定的，无法避免。

3-1-4. 深浅层网络选择

是否选择浅层神经网络还是深层网络取决于具体的任务和数据。浅层神经网络通常适用于简单的模式识别任务，具有较少的参数和计算量，易于训练和解释。而深层网络在处理复杂的任务和大规模数据集时具有更强的表达能力，可以学习到更高层次的抽象特征。然而，深层网络也面临着更难训练、容易过拟合等挑战，因此需要更多的数据和更复杂的优化技巧。

3-1-5. Sigmoid, ReLU, Tanh

• Sigmoid

$$
f(x) = \frac{1}{1+ exp(-x)} \
f’(x) = f(x)(1-f(x))
$$

$$
\begin{aligned}
f’(z) &= (\frac{1}{1+e^{-z}})’
\
&= \frac{e^{-z}}{(1+e^{-z})^{2}}
\
&= \frac{1+e^{-z}-1}{(1+e^{-z})^{2}}
\
&= \frac{1}{(1+e^{-z})}(1-\frac{1}{(1+e^{-z})})
\
&= f(z)(1-f(z))
\
\end{aligned}
$$

优点：

（1）输出范围在(0, 1)之间，适用于二分类问题的输出层。

（2）可以当作“门”

缺点：

（1）需要计算指数，速度慢

（2）会产生梯度消失问题

• Tanh

$$
f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \

f’(x) = 1 - (f(x))^2
$$

优点：

（1）Tanh激活函数的优点是输出范围在(-1, 1)之间，相对于Sigmoid函数具有更大的梯度。

缺点：

（1）需要计算指数，速度慢

（2）会产生梯度消失问题

• Relu

$$
f(x) = max(x,0) \
\begin{equation}
f’(x)=\left{
\begin{aligned}
1,x>0 \
0,x\leq0 \
\end{aligned}
\right.
\end{equation}
$$

优点：

（1）从计算的角度上，sigmoid和tanh都需要计算指数，复杂度高，而ReLU只需要一个阈值就可以得到激活值

（2）ReLU的非饱和性可以有效解决梯度消失的问题，提供相对宽的激活边界

（3）ReLU的单侧抑制提供了网络的稀疏表达能力（防止过拟合）

缺点：

（1）训练过程中会导致神经元死亡的问题。神经元死亡介绍

Leaky ReLU
$$
\begin{equation}
f(x)=\left{
\begin{aligned}
x,x>0 \
ax,x\leq0 \
\end{aligned}
\right.
\end{equation}
\

f’(x)=\left{
\begin{aligned}
1,x>0 \
a,x\leq0 \
\end{aligned}
\right.
$$
优点：实现单侧抑制，又保留了部分附体度信息以致不完全消失

缺点：a值需要人工选择

3-1-6. 常用激活函数

• 常用激活函数的导数如下：

  • Sigmoid函数的导数：σ’(x) = σ(x) * (1 - σ(x))

  • ReLU函数的导数：ReLU’(x) = 1，当输入大于等于零；ReLU’(x) = 0，当输入小于零

  • Tanh函数的导数：tanh’(x) = 1 - tanh^2(x)

3-1-7. 网络参数全部初始化为0?

不应将网络参数全部初始化为0。如果所有参数都相同，则在反向传播过程中，所有参数将以相同的方式更新，导致所有隐藏单元对输入的响应也是相同的，无法发挥神经网络的表达能力。因此，应该使用一些合适的初始化方法来打破对称性，如随机初始化或者Xavier初始化。

3-1-8. Batchsize大小

Batchsize大小会影响收敛速度。较大的Batchsize可以提高训练过程的稳定性，减小每个样本的噪声影响，从而使训练过程更加平滑。然而，较大的Batchsize也意味着每个参数更新的计算量增加，可能导致训练速度变慢。另外，较小的Batchsize可以提供更多的随机性，有助于跳出局部最优解，但也容易受到噪声的干扰。因此，选择合适的Batchsize需要综合考虑计算资源、训练速度和模型性能等因素。

3-2. CNN

3-2-1. 工作原理

卷积神经网络（Convolutional Neural Network，CNN）是一种深度学习模型，主要用于处理具有网格结构数据（如图像）的任务。CNN的工作原理可以简述如下：

1. 输入层：接收原始图像作为输入。
2. 卷积层：使用多个卷积核对输入图像进行卷积操作。每个卷积核会在输入图像上滑动，通过计算滑动窗口内的元素与卷积核的乘积之和，生成新的特征图。
3. 激活函数层：对卷积层的输出进行非线性映射，常用的激活函数包括ReLU（Rectified Linear Unit）。
4. 池化层：对特征图进行下采样操作，减少特征图的尺寸并保留重要的特征。常用的池化操作有最大池化（Max Pooling）和平均池化（Average Pooling）。
5. 全连接层：将池化层的输出展平成一维向量，然后通过全连接层进行分类或回归等任务。
6. 输出层：根据具体任务选择适当的输出层，如Softmax层进行分类问题的概率输出。

3-2-2. 卷积核

• 卷积核是CNN中的重要组件，它是一个小的矩阵（通常是正方形），用于提取图像中的特征。选择大卷积核和小卷积核会对CNN的性能和特征提取能力产生影响。

• 大卷积核具有较大的感受野（receptive field），可以捕捉更大范围的特征信息。它适用于处理较大尺寸的目标或图像中的全局特征。然而，使用大卷积核会导致模型参数增加和计算量增加，可能需要更多的存储和计算资源。小卷积核具有较小的感受野，适用于捕捉局部细节和纹理特征。使用小卷积核可以减少模型参数和计算量，但可能会丢失一些全局信息。

• 根据任务和数据集的特点，可以根据需要选择合适的卷积核大小。通常，在网络的早期层使用较小的卷积核进行局部特征提取，而在后续层使用较大的卷积核进行全局特征提取。

3-2-3. 设计卷积核

• 卷积核设计通常需要根据任务和数据集的特点进行调试和优化。以下是一些常见的设计方法：

  • 手动设计：根据经验和先验知识，设计卷积核的形状和参数。例如，可以设计边缘检测器、纹理过滤器等特定的卷积核来提取相应的特征。
  • 自动化搜索：使用自动化方法，如遗传算法或强化学习，来搜索最优的卷积核。这种方法可以通过在训练过程中对卷积核进行优化来提高模型性能。
  • 迁移学习：使用预训练的卷积核，如在大规模图像数据集上训练的卷积核（如ImageNet），然后根据具体任务微调这些卷积核。这种方法可以利用预训练模型的特征提取能力来加速训练和提高性能。

• 设计卷积核是一个复杂的任务，需要结合具体问题和数据集进行实验和调试，以获得最佳的性能。

3-2-4. 平移不变性

• CNN具有平移不变性，这是由于卷积操作的特性。在CNN中，卷积核在输入图像上滑动进行特征提取。由于卷积核的权重是共享的，它对输入图像的不同位置具有相同的响应模式。具体而言，当卷积核检测到某种特征时，不论这个特征在输入图像的哪个位置出现，卷积核都会生成相应的响应。这种共享权重的特性使得CNN对输入图像的平移具有不变性。换句话说，如果输入图像中的某个特征在不同位置出现，CNN会对这些位置产生相似的响应。

• 平移不变性使得CNN在处理图像时能够更好地捕捉到图像中的局部特征，而不受其具体位置的影响。这对于许多计算机视觉任务（如目标检测和图像分类）是非常有用的。

3-2-5. 池化

• 池化操作是CNN中常用的一种操作，用于减小特征图的尺寸并提取重要的特征。池化操作的作用包括：

  • 下采样：通过减小特征图的尺寸，降低了后续层的计算复杂度。同时，它可以保留重要的特征信息，减少冗余和噪声。
  • 平移不变性：池化操作可以使特征图对平移具有一定程度的不变性，类似于卷积操作。它可以帮助模型更好地处理输入图像中的局部特征，而不受其具体位置的影响。

• 常用的池化操作包括最大池化（Max Pooling）和平均池化（Average Pooling）。最大池化从每个池化窗口中选择最大值作为池化后的值，而平均池化计算每个窗口中的平均值。这些操作在保留重要特征的同时，减小了特征图的尺寸，提高了计算效率。

将Pooling核覆盖区域中所有值的平均值（最大值）作为汇合结果。average-pooling，Max-polling，stochastic-polling（对输入数据中的元素按照一定概率大小随机选择，元素值大的activattion被选中的概率大）Pooling操作后的结果相比起输入减小了，是一种降采样操作。pooling层的作用

1. 特征不变性（feature invariant）。pooling操作使模型更关注是否存在某些特征而不是特征具体的位置。

2. 数据降维。降采样的操作使模型可以抽取更广范围的特征，同时减小了下一层输入大小，进而减少计算量和参数个数。

3-2-6. 为什么需要Pooling

CNN需要池化操作的原因主要有两个方面：

1. 特征降维：通过池化操作可以减小特征图的尺寸，从而减少后续层的计算复杂度。这对于深层网络而言尤为重要，因为随着网络层数的增加，特征图的尺寸会逐渐增大，导致计算和存储资源需求增加。
2. 平移不变性：池化操作可以使特征图对平移具有一定程度的不变性，类似于卷积操作。这对于处理图像中的局部特征是有益的，因为它可以使模型更好地捕捉到这些特征，而不受其具体位置的影响。

需要注意的是，随着深度学习的发展，一些最新的网络结构和任务中已经较少使用池化操作，而是通过卷积操作和其他技术来实现特征降维和平移不变性。

3-2-7. Batch Normalization

• Batch Normalization（批归一化）是一种常用的深度学习技术，用于加速模型的训练过程并提高模型的鲁棒性。它通过对网络的每一层的输入进行归一化，使得输入具有零均值和单位方差的分布。Batch Normalization的原理如下：

  1. 归一化：对于每个小批量样本的输入，计算其均值和方差。然后，使用批量的均值和方差对输入进行归一化，使其具有零均值和单位方差。
  2. 重缩放和平移：将归一化后的输入进行线性变换，通过乘以一个可学习的缩放因子（scale）和加上一个可学习的平移因子（shift）来恢复数据的表示能力。

• Batch Normalization的使用通常在卷积神经网络（CNN）中，在卷积层或全连接层的输出之后、激活函数之前进行。它可以作为网络的一部分，在训练过程中以端到端的方式进行优化。Batch Normalization的优点和作用包括：

  • 加速训练：通过归一化输入，Batch Normalization可以降低网络训练的收敛时间。它可以减少梯度消失和梯度爆炸问题，使得网络更容易学习。
  • 提高模型的鲁棒性：Batch Normalization对输入的小扰动具有一定的鲁棒性。这可以提高模型在测试数据上的泛化能力，减少过拟合的风险。
  • 允许使用更高的学习率：由于归一化的作用，Batch Normalization可以允许使用更高的学习率，加快模型的收敛速度。
  • 减少对参数初始化的依赖：Batch Normalization对网络的参数初始化相对不敏感，可以减少手动调整参数初始化的工作量。
  • 正则化效果：Batch Normalization在一定程度上具有正则化的效果，可以抑制模型的过拟合。

• 需要注意的是，Batch Normalization在训练过程和推理过程中的行为是不同的。在训练过程中，Batch Normalization使用每个小批量样本的均值和方差进行归一化。而在推理过程中，通常使用整个训练集的均值和方差进行归一化，或者使用移动平均的方式来估计均值和方差。

3-2-8. 卷积操作的本质

• 卷积操作的本质特性包括稀疏交互和参数共享。

  • 稀疏交互（Sparse Interaction）：在卷积操作中，卷积核的大小相对于输入图像来说很小。这意味着每个卷积核只与输入图像的一小部分区域进行交互。这种局部连接的方式可以减少模型的参数数量和计算量，提高模型的效率。
  • 参数共享（Parameter Sharing）：在CNN中，每个卷积核的权重被共享到整个输入图像的不同位置。这意味着卷积核学习到的特征在输入图像的不同位置具有相同的响应模式。通过参数共享，CNN可以更好地捕捉输入图像中的局部特征，并且可以在不同位置共享相同的特征提取能力。

• 稀疏交互和参数共享使得CNN能够有效地处理具有网格结构的数据，如图像。它们减少了模型的复杂性，并且可以提高模型的泛化能力。稀疏交互和参数共享利用了图像中的局部相关性和平移不变性，使得CNN能够自动学习到图像的特征，并且在不同位置和尺度上具有良好的泛化能力。

3-2-9. Fine-tuning（微调）

​ Fine-tuning是指在已经训练好的模型基础上，针对特定任务或数据集进行进一步的训练。一般情况下，已经训练好的模型是在大规模数据集上进行训练得到的，而微调则是为了适应一个特定的、相关的任务或数据集。

• 微调的一般步骤如下：

  1. 基础模型选择：选择一个在相关任务或数据集上表现良好的预训练模型作为基础模型。这个预训练模型可以是在大规模数据集上训练得到的，如ImageNet上的预训练模型。
  2. 冻结参数：将基础模型的参数固定住，不进行更新。这样可以保持基础模型已经学到的特征表示不变。
  3. 替换或添加新的输出层：根据特定的任务或数据集需求，替换或添加新的输出层。新的输出层的结构要与任务相匹配，通常包括最后的分类层。
  4. 解冻部分参数：为了适应特定任务或数据集，可以选择解冻部分参数，使其可以在微调过程中进行更新。一般来说，解冻的参数主要是与新的输出层相连的部分，以便让模型能够在新任务上进行更好的学习。
  5. 微调训练：使用特定任务或数据集的训练集对模型进行微调训练。在微调过程中，一般会使用较小的学习率，以避免破坏基础模型已经学到的特征表示。

• 微调的一些常用技巧包括：

  • 选择合适的基础模型：基础模型应该在相关任务或数据集上表现良好，具有较好的泛化能力。

  • 适当的参数解冻：解冻的参数应该与特定任务相关，以便模型可以在新任务上进行有效的学习。

  • 适当调整学习率：微调过程中，可以使用较小的学习率，以避免过大的参数更新对已学到的特征造成破坏。

  • 数据增强：在微调过程中，可以使用数据增强技术来扩充训练集，增加模型的泛化能力。

  • 提前停止：在微调过程中，可以根据验证集的性能来确定停止训练的时机，以避免过拟合。

总之，微调是一种利用已经训练好的模型来适应特定任务或数据集的技术。通过合理选择基础模型、适当调整参数和训练策略，微调可以在特定任务上取得更好的性能。

3-2-10. CNN每个神经元学到了什么

观察CNN每个神经元学到的特征是一项重要的任务，可以帮助我们理解CNN的工作原理、验证网络的有效性以及进行模型的解释性分析。以下是几种常见的方法来观察CNN每个神经元学到的特征：

1. 可视化滤波器：CNN的卷积层中的每个神经元通常对应一个滤波器，可以通过可视化滤波器的权重来观察神经元学到的特征。将滤波器权重以图像的形式展示出来，可以看到神经元所感受的输入模式。例如，在图像分类任务中，可以可视化第一层卷积层的滤波器，观察它们是否学到了边缘、纹理等低级特征。
2. 可视化激活图：通过可视化卷积层输出的激活图，可以观察到每个神经元在输入上的响应模式。选择感兴趣的神经元，将其激活图可视化为热力图或者灰度图，可以看到神经元对输入图像的感兴趣的区域。这可以帮助我们理解神经元在图像中学到的具体特征，比如边缘、纹理、形状等。
3. 特征重要性分析：可以通过特征重要性分析的方法来判断每个神经元对于模型的预测结果的贡献程度。常见的方法包括梯度类方法（如梯度类激活图和梯度类权重）和基于掩码的方法（如LIME和SHAP）。这些方法可以帮助我们确定哪些输入特征对于模型的决策是重要的，从而间接了解每个神经元所学到的特征。
4. 可视化输入重建：通过优化输入图像，使得该图像能够最大程度地激活目标神经元。这种方法称为输入重建或反卷积，通过反向传播梯度来调整输入图像，使得最终的激活最大化。这样可以生成一个与目标神经元高度关联的输入图像，进而理解该神经元所学到的特定特征。

需要注意的是，CNN是一种高度非线性的模型，神经元的响应很难直接解释。因此，以上方法只能提供一些关于神经元学习特征的直观理解，而无法完全揭示网络的内部工作原理。此外，观察单个神经元的学习特征可能只是整个网络的一小部分，深度学习模型的工作是通过整个网络的组合和协同来实现的。因此，理解CNN的学习和决策过程仍然是一个开放性的研究问题。

3-3. RNN

3-3-1. RNN模型原理

RNN（循环神经网络）模型原理是一种能够处理序列数据的神经网络模型。它通过引入时间维度的循环连接，使得网络可以在处理当前输入时保留之前的信息状态。RNN适合解决需要考虑上下文关系和历史信息的问题，例如自然语言处理中的语言建模、机器翻译、语音识别等任务。RNN的循环结构使其能够捕捉序列中的时间依赖关系。

3-3-2. RNN v.s. DNN

RNN（循环神经网络）和DNN（深度神经网络）的主要区别在于网络结构。RNN具有循环连接，允许信息在网络内部进行传递和共享，以处理序列数据。DNN则是一种前向传播的结构，每一层的输入只依赖于前一层的输出。RNN适用于处理序列数据，而DNN更适用于处理独立和无序的数据。

3-3-3. 记忆功能？

RNN有记忆功能的原因在于其循环结构。RNN的隐藏状态可以捕捉到之前时间步的输入信息，随着时间的推移，可以将过去的信息传递到当前时间步，实现了记忆功能。这使得RNN可以处理具有时间依赖性的任务，同时也是其在序列数据建模中的关键。

3-3-4. 长短期记忆网络

长短期记忆网络（LSTM）通过引入门控机制来实现长短期记忆功能。LSTM包含三个主要的门：输入门（input gate）、遗忘门（forget gate）和输出门（output gate）。输入门控制新的输入信息的流入，遗忘门控制之前的记忆是否被遗忘，输出门控制输出的记忆。通过这些门的控制，LSTM可以在长序列中选择性地保留和遗忘信息，从而实现对长期依赖性的建模。

LSTM可以对有价值的信息进行长期记忆，与RNN不同的是，LSTM记忆单元c的转移不一定完全取决于激活函数计算得到的状态，还由输入门和遗忘门共同控制。在一个训练好的LSTM模型中，当输入序列中没有重要信息时，遗忘门的值接近于1，输入门的值接近于0，表示过去的记忆被完整保存，而输入信息被放弃，从而实现长期记忆功能。

当输入序列中存在重要信息时，LSTM应把他存入记忆中，此时输入门接近于1。当输入序列中存在重要信息且该信息意味着之前的记忆不再重要时，输入门的值接近1，遗忘门的值接近0。

3-3-5. LSTM激活函数

长短期记忆网络（LSTM）的各模块通常使用sigmoid激活函数来控制门的开关，以及tanh激活函数来调节记忆单元的状态。这是经典的LSTM结构所使用的激活函数组合。但理论上，也可以尝试其他激活函数，根据任务需求进行调整。

百面p245。输入门、输出门、遗忘门使用sigmoid函数作为激活函数；在生成候选记忆时，使用双曲正切函数Tanh作为激活函数。首先这两个激活函数都是饱和的，如果使用非饱和函数如ReLU，将难以实现门控的效果。

sigmoid作为门控信号的原因：sigmoid函数的输出在01之间，符合门控的物理定义。并且是饱和的，当输入较大或者较小时，其输出会非常接近1或0，从而保证该门的开或关。Tanh用于生成候选记忆的原因：输出在 -11之间，这与大多数场景下特征分布式以0为中心相吻合；并且Tanh函数在输入为0附近相比sigmoid有更大的梯度，通常使模型收敛更快。

3-3-6. GRU v.s. LSTM

GRU（门控循环单元）和LSTM（长短期记忆网络）是两种常用的循环神经网络模型，它们在解决长期依赖问题上有一些异同。相比于LSTM，GRU的结构更为简单，只包含了两个门：更新门（update gate）和重置门（reset gate）。GRU通过这两个门的控制，实现了对过去信息的记忆和遗忘，同时降低了参数的复杂性。LSTM相比之下具有更多的门控单元，因此在某些复杂任务上可能表现更优，但在参数量和计算复杂度上也更高。

• 相同点

  • 都会有门操作，决定是否保留上时刻的状态，和是否接收此时刻的外部输入，LSTM 是用遗忘门（forget gate $f_t$）和输入门（input gate $i_t$）来做到的，GRU 则是只用了一个更新门（update gate $z_t$ ）
  • 遗忘门或者更新门选择不重写（overwritten）内部的 memory，那么网络就会一直记住之前的重要特征，那么会对当前或者未来继续产生影响。缓解梯度消失。

• 不同点

  • 首先就是 LSTM 有一个输出门来控制 memory content 的曝光程度（exposure），而 GRU 则是直接输出。
  • 另一点是要更新的 new memory content 的来源也不同。$\tilde{h}{t}$会通过重置门（reset gate） 控制从$h{t-1}$ 中得到信息的力度，而 $\tilde{c}{t}$ 则没有，而是直接输入$h{t-1}$。
  • 相同个数参数的情况下，GRU 会比 LSTM 稍好一些

3-3-7. Seq2Seq模型

Seq2Seq模型是指序列到序列（Sequence-to-Sequence）模型，也称为编码器-解码器（Encoder-Decoder）模型。它适用于将一个序列作为输入，经过编码器进行特征提取和表示，然后通过解码器生成另一个序列作为输出。Seq2Seq模型能够处理机器翻译、文本摘要、对话生成等问题，其中输入和输出序列的长度可以不同。在经典的实现中，编码器和解码器各由一个循环神经网络构成，两个循环神经网络是共同训练的。解决问题：机器翻译、语音识别、自动对话。

3-3-8. 注意力机制

• 注意力机制是一种用于增强序列到序列（Sequence-to-Sequence）模型性能的技术。它的主要目的是在解码器生成输出序列时，对输入序列中不同位置的信息赋予不同的权重或注意力。通过引入注意力机制，Seq2Seq模型可以更加准确地对输入序列进行建模，并在生成输出序列时更好地关注相关的输入部分。注意力机制的引入主要解决了输入和输出序列之间的对齐问题，以及处理长序列时的信息衰减问题。

• 编码-解码架构的主要缺点：编码器RNN输出的上下文C的维度太小，难以恰当的概括一个长的输入序列的完整信息。注意力机制主要解决问题：

  • 随着输入序列增长，模型性能发生显著下降。因为编码时输入序列的全部信息压缩到了一个定长向量表示中。随着序列增长，句子越前面的词的信息丢失就越严重。
  • seq2seq输出序列中，常常会损失部分输入序列的信息。这是因为在解码时，当前词及对应的源语言词的上下文信息和位置信息在编解码过程中丢失了。

attention 本身可以理解为一种对齐关系，给出了模型输入、输出之间的对齐关系，解释了模型到底学到了什么知识。

• Attention分类

  • global attention vs local attention

    上述的 attention 机制中为了计算上下文向量 $\overrightarrow{\mathbf{c}}{i}$， 需要考虑 encoder 的所有隐向量（global attention）。当输入序列较长时（如一段话或一篇文章），计算效率较低。local attention 在计算上下文向量 $\overrightarrow{\mathbf{c}}{i}$ 时只需要考虑 encoder 的部分隐向量：首选预测encoder 端对齐的位置 $p_{i}$，然后基于位置 $p_{i}$ 选择一个窗口来计算上下文向量 $\overrightarrow{\mathbf{c}}_{i}$ 。

  • self attention

    传统的 attention 是基于encoder 端和 decoder 端的隐向量来计算 attention的，得到的是输入序列的每个 input 和输出序列的每个 output 之间的依赖关系。self attention 计算三种 attention：

    • 在encoder 端计算自身的 attention，捕捉input 之间的依赖关系。
    • 在 decoder 端计算自身的 attention，捕捉output 之间的依赖关系。
    • 将 encoder 端得到的 self attention 加入到 decoder 端得到的 attention中，捕捉输入序列的每个 input 和输出序列的每个 output 之间的依赖关系。

3-3-9. RNN的长期依赖问题

• RNN的长期依赖（Long-Term Dependencies）问题是指在处理长序列数据时，网络难以有效地记住过去的信息，导致难以捕捉到远距离的依赖关系。这是因为RNN的梯度在反向传播过程中会不断地乘以一个权重，导致梯度指数级地增大或减小，从而产生梯度消失或梯度爆炸的问题。解决方法：
  • LSTM、GRU等模型加入门控机制，捕捉长期记忆，很大程度上弥补了梯度消失
  • 残差结构
  • 设计多个时间尺度的模型：在细粒度的时间尺度上处理近期信息、在粗粒度时间尺度上处理远期的信息。得到粗粒度时间尺度方法1跳跃链接：增加从远期的隐变量到当前隐变量的直接连接；2. 是删除连接：主动删除时间跨度为 1 的连接，并用更长的连接替换。

3-3-10. RNN梯度爆炸/消失问题

主要由于权重矩阵 $W$ 在不同时间步被重复使用，导致形成 $W$ 的幂乘

1. 长期依赖的问题是深度学习中的一个主要挑战，其产生的根本问题是：经过许多阶段传播之后，梯度趋向于消失或者爆炸。

   • 长期依赖的问题中，梯度消失占大部分情况，而梯度爆炸占少数情况。但是梯度爆炸一旦发生，就优化过程影响巨大。
   • RNN 涉及到许多相同函数的多次复合作用，每个时间步一次。这种复合作用可以导致极端的非线性行为。因此在RNN 中，长期依赖问题表现得尤为突出。

2. 考虑一个没有非线性、没有偏置非常简单的循环结构： $\overrightarrow{\mathbf{h}}^{(t)}=\mathbf{W} \overrightarrow{\mathbf{h}}^{(t-1)}$。则有：

   

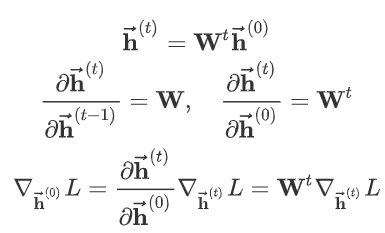
   设$\mathbf{N}$ 可以正交分解时： $\mathbf{W}=\mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{T}$ 。其中 0 为正交矩阵，$\mathbf{\Lambda}$ 为特征值组成的三角阵。则：
   $$
   \begin{array}{c}{\overrightarrow{\mathbf{h}}^{(t)}=\mathbf{Q} \mathbf{\Lambda}^{t} \mathbf{Q}^{T} \overrightarrow{\mathbf{h}}^{(0)}} \ {\nabla_{\overrightarrow{\mathbf{h}}^{(0)}} L=\frac{\partial \overrightarrow{\mathbf{h}}^{(t)}}{\partial \overrightarrow{\mathbf{h}}^{(0)}} \nabla_{\overrightarrow{\mathbf{h}}^{(t)}} L=\mathbf{Q} \mathbf{\Lambda}^{t} \mathbf{Q}^{T} \nabla_{\overrightarrow{\mathbf{h}}^{(t)}} L}\end{array}
   $$

   • 前向传播：

     • 对于特征值的幅度不到 1 的特征值对应的 $\overrightarrow{\mathbf{h}}^{(0)}$ 的部分将随着 $t$ 衰减到 0 。
     • 对于特征值的幅度大于 1 的特征值对应的$\overrightarrow{\mathbf{h}}^{(0)}$ 的部分将随着$t$ 指数级增长。

   • 反向传播：

     • 对于特征值幅度不到1的梯度的部分将随着$t$ 衰减到 0 。

     • 对于特征值幅度大于1的梯度的部分将随着 $t$ 指数级增长 。

3. 若考虑非线性和偏置，即： $\overrightarrow{\mathbf{h}}^{(t+1)}=\tanh \left(\overrightarrow{\mathbf{b}}+\mathbf{W} \overrightarrow{\mathbf{h}}^{(t)}+\mathbf{U} \overrightarrow{\mathbf{x}}^{(t+1)}\right)$，有：
   $$
   \frac{\partial \overrightarrow{\mathbf{h}}^{(t+1)}}{\partial \overrightarrow{\mathbf{h}}^{(t)}}=\operatorname{diag}\left(1-\left(\overrightarrow{\mathbf{h}}^{(t+1)}\right)^{2}\right) \mathbf{w}
   $$

   • 前向传播：

     由于每一级的 $\overrightarrow{\mathbf{h}}$ 的幅度被 $\tanh (\cdot)$ 函数限制在 (-1,1) 之间，因此前向传播并不会指数级增长。

     这也是为什么 RNN 使用 tanh 激活函数，而不使用 relu的原因。

   • 反向传播：

     由于隐状态的幅度被$\tanh (\cdot)$ 函数限制在 (-1,1) 之间，因此 $\operatorname{diag}\left(1-\left(\overrightarrow{\mathbf{h}}^{(t+1)}\right)^{2}\right) \mathbf{W}$ 对 $\mathbf{W}$进行了一定程度上的缩小。$\overrightarrow{\mathbf{h}}^{(t+1)}$ 越大，结果越小。

     • 如果 $\mathbf{W}$ 的特征值经过这样的缩小之后，在每个时刻都远小于1（因为每个时刻缩小的比例会变化），则该梯度部分将衰减到 0 。
     • 如果 $\mathbf{W}$ 的特征值经过这样的缩小之后，在每个时刻都远大于1，则该梯度部分将指数级增长。
     • 如果 $\mathbf{W}$ 的特征值经过这样的缩小之后，在不同的时刻有时候小于1有时候大于1（因为每个时刻缩小的比例会变化），则该梯度部分将比较平稳。

3-3-11. 梯度爆炸问题解决

为了解决RNN中的梯度爆炸问题，可以采用梯度截断（Gradient Clipping）的方法。梯度截断通过设置一个阈值，当梯度的范数超过该阈值时，将梯度缩放至阈值以内。这样可以避免梯度爆炸问题，并保持梯度的方向不变。

3-3-12. 梯度消失问题解决

RNN中的梯度消失问题可以通过使用门控循环单元（GRU）或长短期记忆网络（LSTM）等结构来缓解。这些结构引入了门控机制，可以选择性地更新和保留信息。通过控制门的开关，网络可以更好地捕捉长期依赖关系，从而解决了梯度消失问题。

3-3-13. LSTM结构

经典的LSTM中第t步计算公式为
$$
\begin{array}{l}{i_{t}=\sigma\left(W_{i} x_{t}+U_{i} h_{t-1}+b_{i}\right)} \ {f_{t}=\sigma\left(W_{f} x_{t}+U_{j} h_{t-1}+b_{f}\right)} \ {o_{t}=\sigma\left(W_{\sigma} x_{t}+U_{o} h_{t-1}+b_{o}\right)} \ {\tilde{c}{t}=\operatorname{Tanh}\left(W{c} x_{t}+U_{c} h_{t-1}\right)} \ {c_{t}=f_{t} \odot c_{t-1}+i_{t} \odot \tilde{c}{t}} \ {h{t}=o_{t} \odot \tanh \left(c_{t}\right)}\end{array}
$$

3-3-14. LSTM变种有哪些

“peephole connection”：让 门控层 也会接受细胞状态的输入。

coupled forget and input gates：将输入门和遗忘们耦合在一起，输入和遗忘是同步的。

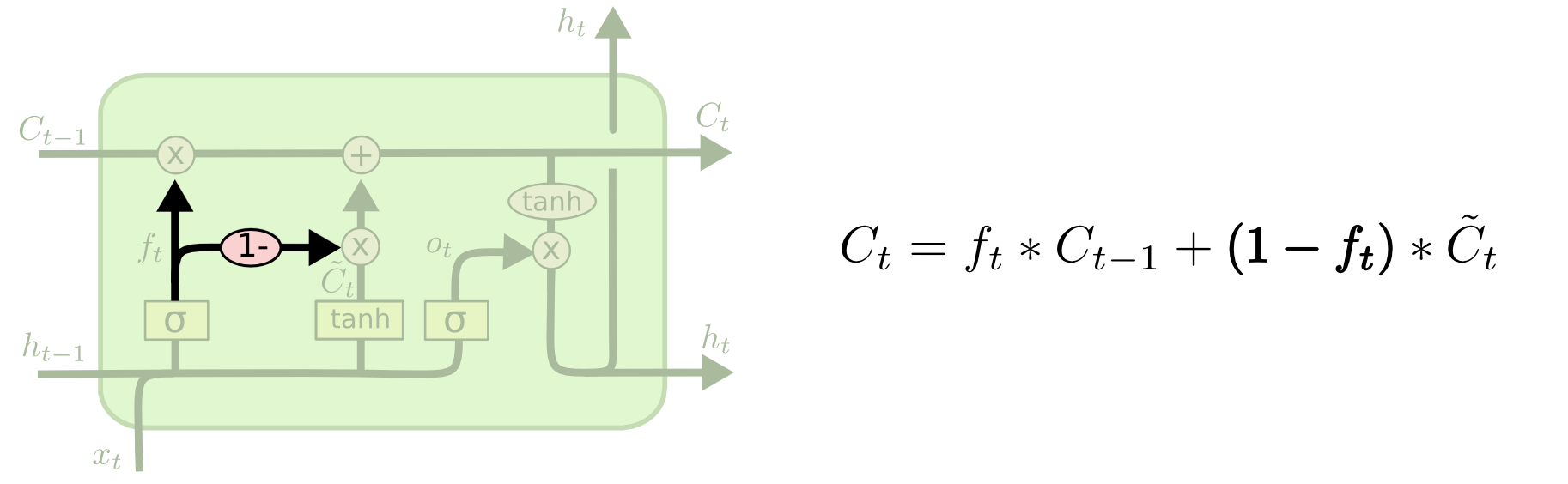
3-3-15. LSTM解决梯度消失

将连乘关系转换为相加的线性关系

在LSTM中 $c_{t}=f_{t} \odot c_{t-1}+i_{t} \odot \tilde{c}{t}$ ，其中 $c{t-1}$是此前的信息， $\tilde{\mathbf{c}}{t}$是当前即刻的新信息， $c_t$ 是最终的信息。可以看到 $c_t$和 $c{t-1}$此时是线性关系，不再是RNN中的连乘关系，梯度以线性在中间节点流动，因此可以保证很长时间的记忆。

进一步地，如果门控信号考虑bias，同时忽略输入变量 $h_{j-1}$的作用，隐含层关系表示为：
$$
c_{j}=\sigma\left(W^{f} X_{j}+b^{f}\right) c_{j-1}+\sigma\left(W^{i} X_{j}+b^{i}\right) \sigma\left(W X_{j}+b\right)
$$
于是，需要连乘的项表示为：
$$
\frac{\partial c_{j}}{\partial c_{j-1}}=\sigma\left(W^{f} X_{j}+b\right)
$$
该值范围在0~1之间。但是在实际参数更新中，可以通过控制bias比较大，使得该值接近于1；在这种情况下，即使通过很多次连乘的操作，梯度也不会消失，仍然可以保持“长距”连乘项的存在。即总可以通过选择合适的参数，在不发生梯度爆炸的情况下，找到合理的梯度方向来更新参数，而且这个方向可以充分地考虑远距离的隐含层信息的传播影响。

References

1. Machine Learning Interview Repo
2. 小萌讲的嘎嘎好
3. KnowingAI知智也讲的嘎嘎好