D2L-12-Optimization Algorithms
本文最后更新于:7 个月前
对于深度学习问题,我们通常会先定义损失函数。一旦我们有了损失函数,我们就可以使用优化算法来尝试最小化损失。在优化中,损失函数通常被称为优化问题的目标函数。按照传统惯例,大多数优化算法都关注的是最小化。如果我们需要最大化目标,那么有一个简单的解决方案:在目标函数前加负号即可。
优化和深度学习
优化的目标
- 本质上,优化和深度学习的目标是根本不同的。前者主要关注的是最小化目标,后者则关注在给定有限数据量的情况下寻找合适的模型。
- 训练误差和泛化误差通常不同:由于优化算法的目标函数通常是基于训练数据集的损失函数,因此优化的目标是减少训练误差。但是,深度学习(或更广义地说,统计推断)的目标是减少泛化误差。为了实现后者,除了使用优化算法来减少训练误差之外,我们还需要注意过拟合。
深度学习中的优化挑战
- 在深度学习中,大多数目标函数都很复杂,没有解析解。相反,我们必须使用数值优化算法。本章中的优化算法都属于此类别。深度学习优化存在许多挑战。其中最令人烦恼的是局部最小值、鞍点和梯度消失。
局部最小值
- 对于任何目标函数$f(x)$,如果在x处对应的$f(x)$值小于在x附近任意其他点的$f(x)$值,那么$f(x)$可能是局部最小值。如果$f(x)$在x处的值是整个域中目标函数的最小值,那么$f(x)$是全局最小值。
深度学习模型的目标函数通常有许多局部最优解。当优化问题的数值解接近局部最优值时,随着目标函数解的梯度接近或变为零,通过最终迭代获得的数值解可能仅使目标函数局部最优,而不是全局最优。只有一定程度的噪声可能会使参数跳出局部最小值。事实上,这是小批量随机梯度下降的有利特性之一。在这种情况下,小批量上梯度的自然变化能够将参数从局部极小值中跳出。
- 通常情况下,都是局部最小值!
看看凸函数的性质第一条:凸函数的局部极小值是全局极小值。
- 我们学过的函数:
- 只有线性回归和Softmax是凸函数
- 其他的都是非凸函数
适用场景十分有限!!!
鞍点
- 除了局部最小值之外,鞍点是梯度消失的另一个原因。鞍点(saddle point)是指函数的所有梯度都消失但既不是全局最小值也不是局部最小值的任何位置。
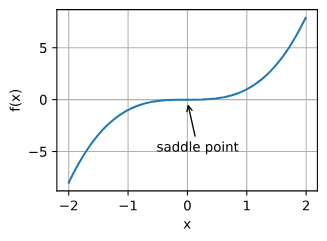
较高维度的鞍点甚至更加隐蔽。
梯度消失
- 可能遇到的最隐蔽问题是梯度消失。在我们取得进展之前,优化将会停滞很长一段时间。事实证明,这是在引入ReLU激活函数之前训练深度学习模型相当棘手的原因之一。
正如我们所看到的那样,深度学习的优化充满挑战。幸运的是,有一系列强大的算法表现良好,即使对于初学者也很容易使用。此外,没有必要找到最优解。局部最优解或其近似解仍然非常有用。
凸性
- 凸性(convexity)在优化算法的设计中起到至关重要的作用, 这主要是由于在这种情况下对算法进行分析和测试要容易。 换言之,如果算法在凸性条件设定下的效果很差, 那通常我们很难在其他条件下看到好的结果。 此外,即使深度学习中的优化问题通常是非凸的, 它们也经常在局部极小值附近表现出一些凸性。 这可能会产生一些像 (Izmailov et al., 2018)这样比较有意思的新优化变体。
定义
我们需要定义凸集(convex sets)和凸函数(convex functions)。
凸集
- 凸集(convex set)是凸性的基础。 简单地说,如果对于任何$a, b \in \mathcal{X}$,连接a和b的线段也位于$\mathcal{X}$中,则向量空间中的一个集合$\mathcal{X}$是凸(convex)的。在数学术语上,这意味着对于所有$\lambda \in [0, 1]$,我们得到
$$
\lambda a + (1-\lambda) b \in \mathcal{X} \text{ 当 } a, b \in \mathcal{X}.
$$
第一组是非凸的,另外两组是凸的。
- 假设$\mathcal{X}$和$\mathcal{Y}$是凸集,那么$\mathcal {X} \cap \mathcal{Y}$也是凸的。
- 假设$\mathcal{X}$和$\mathcal{Y}$是凸集,那么$\mathcal{X} \cup \mathcal{Y}$不一定是凸的,即非凸(nonconvex)的。
凸函数
- 现在我们有了凸集,我们可以引入凸函数(convex function)f。 给定一个凸集X,如果对于所有$x, x’ \in \mathcal{X}$和所有$\lambda \in [0, 1]$,函数$f: \mathcal{X} \to \mathbb{R}$是凸的,我们可以得到:
$$
\lambda f(x) + (1-\lambda) f(x’) \geq f(\lambda x + (1-\lambda) x’).
$$
余弦函数为非凸的,而抛物线函数和指数函数为凸的。
性质
局部极小值是全局极小值
- 首先凸函数的局部极小值也是全局极小值。 -> 反证法可以证明:反证法证明局部极小值是全局极小值
凸函数的下水平集是凸的
- 我们可以方便地通过凸函数的下水平集(below sets)定义凸集。 具体来说,给定一个定义在凸集X上的凸函数f,其任意一个下水平集是凸的。 -> 可以简单证明:证明下水平集是凸的
$$
\mathcal{S}_b := {x | x \in \mathcal{X} \text{ and } f(x) \leq b}
$$
凸性和二阶导数
当一个函数的二阶导数$f: \mathbb{R}^n \rightarrow \mathbb{R}$存在时,我们很容易检查这个函数的凸性。 我们需要做的就是检查$\nabla^2f \succeq 0$, 即对于所有$\mathbf{x} \in \mathbb{R}^n$,$\mathbf{x}^\top \mathbf{H} \mathbf{x} \geq 0$. 例如,函数$f(\mathbf{x}) = \frac{1}{2} |\mathbf{x}|^2$是凸的,因为$\nabla^2 f = \mathbf{1}$,即其导数是单位矩阵。 -> 证明函数的凸性是容易检查的
利用上面的引理和一维情况的结果,我们可以证明多维情况: 多维函数$f:\mathbb{R}^n\rightarrow\mathbb{R}$是凸函数,当且仅当$g(z) \stackrel{\mathrm{def}}{=} f(z \mathbf{x} + (1-z) \mathbf{y})$是凸的,这里$z \in [0,1]$,$\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$。 根据一维情况, 此条成立的条件为,当且仅当对于所有$\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$, $g’’ = (\mathbf{x} - \mathbf{y})^\top \mathbf{H}(\mathbf{x} - \mathbf{y}) \geq 0\ \ \ \ (\mathbf{H} \stackrel{\mathrm{def}}{=} \nabla^2f)$。 这相当于根据半正定矩阵的定义,$\mathbf{H} \succeq 0$。
约束
- 凸优化的一个很好的特性是能够让我们有效地处理约束(constraints)。 即它使我们能够解决以下形式的约束优化(constrained optimization)问题:
$$
\begin{split}\begin{aligned} \mathop{\mathrm{minimize~}}_{\mathbf{x}} & f(\mathbf{x}) \
\text{ subject to } & c_i(\mathbf{x}) \leq 0 \text{ for all } i \in {1, \ldots, N}.
\end{aligned}\end{split}
$$
这里$f$是目标函数,$c_i$是约束函数。
拉格朗日函数
求解一个有约束的优化问题是困难的,解决这个问题的一种方法来自物理中相当简单的直觉。 想象一个球在一个盒子里,球会滚到最低的地方,重力将与盒子两侧对球施加的力平衡。 简而言之,目标函数(即重力)的梯度将被约束函数的梯度所抵消(由于墙壁的“推回”作用,需要保持在盒子内)。 请注意,任何不起作用的约束(即球不接触壁)都将无法对球施加任何力。
这里我们简略拉格朗日函数$L$的推导,上述推理可以通过以下鞍点优化问题来表示:
$$
L(\mathbf{x}, \alpha_1, \ldots, \alpha_n) = f(\mathbf{x}) + \sum_{i=1}^n \alpha_i c_i(\mathbf{x}) \text{ where } \alpha_i \geq 0.
$$
这里的变量$\alpha_i(i=1,\ldots,n)$是所谓的拉格朗日乘数(Lagrange multipliers),它确保约束被正确地执行。 选择它们的大小足以确保所有i的$c_i(\mathbf{x}) \leq 0$。 例如,对于$c_i(\mathbf{x}) < 0$中任意x,我们最终会选择$\alpha_i = 0$。 此外,这是一个鞍点(saddlepoint)优化问题。 在这个问题中,我们想要使$L$相对于$\alpha_i$最大化(maximize),同时使它相对于$x$最小化(minimize)。 有大量的文献解释如何得出函数$L(\mathbf{x}, \alpha_1, \ldots, \alpha_n)$。 我们这里只需要知道$L$的鞍点是原始约束优化问题的最优解就足够了。
惩罚
- 一种至少近似地满足约束优化问题的方法是采用拉格朗日函数$L$。除了满足$c_i(\mathbf{x}) \leq 0$之外,我们只需将$\alpha_i c_i(\mathbf{x})$添加到目标函数$f(x)$。 这样可以确保不会严重违反约束。
- 事实上,我们一直在使用这个技巧。 比如权重衰减 4.5节,在目标函数中加入$\frac{\lambda}{2} |\mathbf{w}|^2$,以确保$\mathbf{w}$不会增长太大。 使用约束优化的观点,我们可以看到,对于若干半径$r$,这将确保$|\mathbf{w}|^2 - r^2 \leq 0$。 通过调整$\lambda$的值,我们可以改变$\mathbf{w}$的大小。
- 通常,添加惩罚是确保近似满足约束的一种好方法。 在实践中,这被证明比精确的满意度更可靠。 此外,对于非凸问题,许多使精确方法在凸情况下的性质(例如,可求最优解)不再成立。
投影
- 满足约束条件的另一种策略是投影(projections)。 同样,我们之前也遇到过,例如在 8.5节中处理梯度截断时,我们通过
$$
\mathbf{g} \leftarrow \mathbf{g} \cdot \mathrm{min}(1, \theta/|\mathbf{g}|),
$$
确保梯度的长度以$\theta$为界限。
- 这就是g在半径为$\theta$的球上的投影(projection)。 更泛化地说,在凸集$\mathcal{X}$上的投影被定义为
$$
\mathrm{Proj}\mathcal{X}(\mathbf{x}) = \mathop{\mathrm{argmin}}{\mathbf{x}’ \in \mathcal{X}} |\mathbf{x} - \mathbf{x}’|.
$$
它是$\mathcal{X}$中离$\mathbf{X}$最近的点。
Convex Projections
梯度下降
- 尽管梯度下降(gradient descent)很少直接用于深度学习, 但了解它是理解下一节随机梯度下降算法的关键。 例如,由于学习率过大,优化问题可能会发散,这种现象早已在梯度下降中出现。 同样地,预处理(preconditioning)是梯度下降中的一种常用技术, 还被沿用到更高级的算法中。
- 最简单的迭代求解方法
- 所有样本一起做梯度下降
一维梯度下降
- 一维中的梯度下降给我们很好的启发。 考虑一类连续可微实值函数$f: \mathbb{R} \rightarrow \mathbb{R}$, 利用泰勒展开,我们可以得到
$$
f(x + \epsilon) = f(x) + \epsilon f’(x) + \mathcal{O}(\epsilon^2).
$$
- 即在一阶近似中,$f(x+\epsilon)$可通过x处的函数值$f(x)$和一阶导数$f’(x)$得出。 我们可以假设在负梯度方向上移动的$\epsilon$会减少$f$。 为了简单起见,我们选择固定步长$\eta > 0$,然后取$\epsilon = -\eta f’(x)$。 将其代入泰勒展开式我们可以得到
$$
f(x - \eta f’(x)) = f(x) - \eta f’^2(x) + \mathcal{O}(\eta^2 f’^2(x)).
$$
- 如果其导数$f’(x) \neq 0$没有消失,我们就能继续展开,这是因为$\eta f’^2(x)>0$。 此外,我们总是可以令$\eta$小到足以使高阶项变得不相关。 因此,有:
$$
f(x - \eta f’(x)) \lessapprox f(x).
$$
- 这意味着,如果我们使用
$$
x \leftarrow x - \eta f’(x)
$$
来迭代x,函数$f(x)$的值可能会下降。 因此,在梯度下降中,我们首先选择初始值$x$和常数$\eta > 0$, 然后使用它们连续迭代x,直到停止条件达成。 例如,当梯度$|f’(x)|$的幅度足够小或迭代次数达到某个值时。
- 本质就是往梯度的反方向走了一步
学习率
学习率(learning rate)决定目标函数能否收敛到局部最小值,以及何时收敛到最小值。 学习率$\eta$可由算法设计者设置。 请注意,如果我们使用的学习率太小,将导致x的更新非常缓慢,需要更多的迭代。
相反,如果我们使用过高的学习率,$\left|\eta f’(x)\right|$对于一阶泰勒展开式可能太大。 也就是说, (11.3.1)中的$\mathcal{O}(\eta^2 f’^2(x))$可能变得显著了。 在这种情况下,x的迭代不能保证降低$f(x)$的值。
局部最小值
- 为了演示非凸函数的梯度下降,考虑函数$f(x) = x \cdot \cos(cx)$,其中c为某常数。 这个函数有无穷多个局部最小值。 根据我们选择的学习率,我们最终可能只会得到许多解的一个。 下面的例子说明了(不切实际的)高学习率如何导致较差的局部最小值。
多元梯度下降
- 现在我们对单变量的情况有了更好的理解,让我们考虑一下$\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top$的情况。 即目标函数$f: \mathbb{R}^d \to \mathbb{R}$将向量映射成标量。 相应地,它的梯度也是多元的,它是一个由d个偏导数组成的向量:
$$
\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top.
$$
- 梯度中的每个偏导数元素$\partial f(\mathbf{x})/\partial x_i$代表了当输入$x_i$时f在x处的变化率。 和先前单变量的情况一样,我们可以对多变量函数使用相应的泰勒近似来思考。 具体来说,
$$
f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \mathbf{\boldsymbol{\epsilon}}^\top \nabla f(\mathbf{x}) + \mathcal{O}(|\boldsymbol{\epsilon}|^2).
$$
- 换句话说,在$\boldsymbol{\epsilon}$的二阶项中, 最陡下降的方向由负梯度$-\nabla f(\mathbf{x})$得出。 选择合适的学习率$\eta > 0$来生成典型的梯度下降算法:
$$
\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x}).
$$
自适应方法
- 选择“恰到好处”的学习率$\eta$是很棘手的。 如果我们把它选得太小,就没有什么进展;如果太大,得到的解就会振荡,甚至可能发散。 如果我们可以自动确定$\eta$,或者完全不必选择学习率,会怎么样? 除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法可以帮我们解决这个问题。 虽然由于计算代价的原因,这些方法不能直接应用于深度学习,但它们为如何设计高级优化算法提供了有用的思维直觉,这些算法可以模拟下面概述的算法的许多理想特性。
牛顿法
- 回顾一些函数$f: \mathbb{R}^d \rightarrow \mathbb{R}$的泰勒展开式,事实上我们可以把它写成
$$
f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \boldsymbol{\epsilon}^\top \nabla f(\mathbf{x}) + \frac{1}{2} \boldsymbol{\epsilon}^\top \nabla^2 f(\mathbf{x}) \boldsymbol{\epsilon} + \mathcal{O}(|\boldsymbol{\epsilon}|^3).
$$
为了避免繁琐的符号,我们将$\mathbf{H} \stackrel{\mathrm{def}}{=} \nabla^2 f(\mathbf{x})$定义为f的Hessian,是d×d矩阵。 当d的值很小且问题很简单时,$\mathbf{H}$很容易计算。 但是对于深度神经网络而言,考虑到$\mathbf{H}$可能非常大,$\mathcal{O}(d^2)$个条目的存储代价会很高, 此外通过反向传播进行计算可能雪上加霜。 然而,我们姑且先忽略这些考量,看看会得到什么算法。
$$
\nabla f(\mathbf{x}) + \mathbf{H} \boldsymbol{\epsilon} = 0 \text{ and hence }
\boldsymbol{\epsilon} = -\mathbf{H}^{-1} \nabla f(\mathbf{x}).
$$
也就是说,作为优化问题的一部分,我们需要将Hessian矩阵$\mathbf{H}$求逆。 -> 牛顿法
收敛性分析
- 以部分目标凸函数f为例,分析它们的牛顿法收敛速度。 这些目标凸函数三次可微,而且二阶导数不为零,即$f’’ > 0$。 由于多变量情况下的证明是对以下一维参数情况证明的直接拓展,对我们理解这个问题不能提供更多帮助,因此我们省略了多变量情况的证明。
- 优化研究人员称之为“线性”收敛,而将$\left|e^{(k+1)}\right| \leq \alpha \left|e^{(k)}\right|$这样的条件称为“恒定”收敛速度。 请注意,我们无法估计整体收敛的速度,但是一旦我们接近极小值,收敛将变得非常快。 另外,这种分析要求f在高阶导数上表现良好,即确保f在如何变化它的值方面没有任何“超常”的特性。
预处理
- 计算和存储完整的Hessian非常昂贵,而改善这个问题的一种方法是“预处理”。 它回避了计算整个Hessian,而只计算“对角线”项,即如下的算法更新:
$$
\mathbf{x} \leftarrow \mathbf{x} - \eta \mathrm{diag}(\mathbf{H})^{-1} \nabla f(\mathbf{x}).
$$
虽然这不如完整的牛顿法精确,但它仍然比不使用要好得多。 为什么预处理有效呢? 假设一个变量以毫米表示高度,另一个变量以公里表示高度的情况。 假设这两种自然尺度都以米为单位,那么我们的参数化就出现了严重的不匹配。 幸运的是,使用预处理可以消除这种情况。 梯度下降的有效预处理相当于为每个变量选择不同的学习率(矢量�的坐标)。 我们将在后面一节看到,预处理推动了随机梯度下降优化算法的一些创新。
梯度下降和线搜索
- 梯度下降的一个关键问题是我们可能会超过目标或进展不足, 解决这一问题的简单方法是结合使用线搜索和梯度下降。 也就是说,我们使用$\nabla f(\mathbf{x})$给出的方向, 然后进行二分搜索,以确定哪个学习率$\eta$使$f(\mathbf{x} - \eta \nabla f(\mathbf{x}))$取最小值。
- 有关分析和证明,此算法收敛迅速(请参见 (Boyd and Vandenberghe, 2004))。 然而,对深度学习而言,这不太可行。 因为线搜索的每一步都需要评估整个数据集上的目标函数,实现它的方式太昂贵了。
随机梯度下降
- 随机一次选择n个样本,算平均再下降就很慢!!!
- SGD就是,从这些样本中抽取一个,作为整个batch的均值,进行梯度下降!!!(数学上是合理的,因为随机取的话,期望不变的昂!!!无偏估计?)
随机梯度更新
- 在深度学习中,目标函数通常是训练数据集中每个样本的损失函数的平均值。给定n个样本的训练数据集,我们假设$f_i(\mathbf{x})$是关于索引i的训练样本的损失函数,其中$\mathbf{x}$是参数向量。然后我们得到目标函数
$$
f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{x}).
$$
- x的目标函数的梯度计算为
$$
\nabla f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}).
$$
如果使用梯度下降法,则每个自变量迭代的计算代价为$\mathcal{O}(n)$,它随n线性增长。因此,当训练数据集较大时,每次迭代的梯度下降计算代价将较高。
- 随机梯度下降(SGD)可降低每次迭代时的计算代价。在随机梯度下降的每次迭代中,我们对数据样本随机均匀采样一个索引i,其中$i\in{1,\ldots, n}$,并计算梯度$\nabla f_i(\mathbf{x})$以更新x:
$$
\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f_i(\mathbf{x}),
$$
- 其中$\eta$是学习率。我们可以看到,每次迭代的计算代价从梯度下降的$\mathcal{O}(n)$降至常数$\mathcal{O}(1)$。此外,我们要强调,随机梯度$\nabla f_i(\mathbf{x})$是对完整梯度$\nabla f(\mathbf{x})$的无偏估计,因为:
$$
\mathbb{E}i \nabla f_i(\mathbf{x}) = \frac{1}{n} \sum{i = 1}^n \nabla f_i(\mathbf{x}) = \nabla f(\mathbf{x}).
$$
这意味着,平均而言,随机梯度是对梯度的良好估计。
- 正如我们所看到的,随机梯度下降中变量的轨迹比我们在 11.3节中观察到的梯度下降中观察到的轨迹嘈杂得多。这是由于梯度的随机性质。也就是说,即使我们接近最小值,我们仍然受到通过$\eta \nabla f_i(\mathbf{x})$的瞬间梯度所注入的不确定性的影响。即使经过50次迭代,质量仍然不那么好。更糟糕的是,经过额外的步骤,它不会得到改善。这给我们留下了唯一的选择:改变学习率$\eta$。但是,如果我们选择的学习率太小,我们一开始就不会取得任何有意义的进展。另一方面,如果我们选择的学习率太大,我们将无法获得一个好的解决方案,如上所示。解决这些相互冲突的目标的唯一方法是在优化过程中动态降低学习率。
- 这也是在
sgd步长函数中添加学习率函数lr的原因。在上面的示例中,学习率调度的任何功能都处于休眠状态,因为我们将相关的lr函数设置为常量。
动态学习率
- 用与时间相关的学习率$\eta(t)$取代$\eta$增加了控制优化算法收敛的复杂性。特别是,我们需要弄清$\eta$的衰减速度。如果太快,我们将过早停止优化。如果减少的太慢,我们会在优化上浪费太多时间。以下是随着时间推移调整$\eta$时使用的一些基本策略(稍后我们将讨论更高级的策略):
$$
\begin{split}\begin{aligned}
\eta(t) & = \eta_i \text{ if } t_i \leq t \leq t_{i+1} && \text{分段常数} \
\eta(t) & = \eta_0 \cdot e^{-\lambda t} && \text{指数衰减} \
\eta(t) & = \eta_0 \cdot (\beta t + 1)^{-\alpha} && \text{多项式衰减}
\end{aligned}\end{split}
$$
分段常数*(piecewise constant)场景中,我们会降低学习率,例如,每当优化进度停顿时。这是训练深度网络的常见策略。
或者,我们可以通过指数衰减(exponential decay)来更积极地减低它。不幸的是,这往往会导致算法收敛之前过早停止。一个受欢迎的选择是$\alpha = 0.5$的多项式衰减(polynomial decay)。在凸优化的情况下,有许多证据表明这种速率表现良好。
指数衰减在实践中是什么样子:
正如预期的那样,参数的方差大大减少。但是,这是以未能收敛到最优解$\mathbf{x} = (0, 0)$为代价的。即使经过1000个迭代步骤,我们仍然离最优解很远。事实上,该算法根本无法收敛。另一方面,如果我们使用多项式衰减,其中学习率随迭代次数的平方根倒数衰减,那么仅在50次迭代之后,收敛就会更好。
关于如何设置学习率,还有更多的选择。例如,我们可以从较小的学习率开始,然后使其迅速上涨,再让它降低,尽管这会更慢。我们甚至可以在较小和较大的学习率之间切换。现在,让我们专注于可以进行全面理论分析的学习率计划,即凸环境下的学习率。对一般的非凸问题,很难获得有意义的收敛保证,因为总的来说,最大限度地减少非线性非凸问题是NP困难的。有关的研究调查,请参阅例如2015年Tibshirani的优秀讲义笔记。
凸目标的收敛性分析
参考收敛性分析
随机梯度和有限样本
- 我们有替换地从离散分布中采样n个观测值。随机选择一个元素i的概率是1/n,因此选择它至少一次就是:
$$
P(\mathrm{choose} i) = 1 - P(\mathrm{omit} i) = 1 - (1-1/n)^n \approx 1-e^{-1} \approx 0.63.
$$
- 类似的推理表明,挑选一些样本(即训练示例)恰好一次的概率是
$$
{n \choose 1} \frac{1}{n} \left(1-\frac{1}{n}\right)^{n-1} = \frac{n}{n-1} \left(1-\frac{1}{n}\right)^{n} \approx e^{-1} \approx 0.37.
$$
这导致与无替换采样相比,方差增加并且数据效率降低。因此,在实践中我们执行后者(这是本书中的默认选择)。最后一点注意,重复采用训练数据集的时候,会以不同的随机顺序遍历它。
小批量随机梯度下降
11.3节中使用完整数据集来计算梯度并更新参数, 11.4节中一次处理一个训练样本来取得进展。 二者各有利弊:每当数据非常相似时,梯度下降并不是非常“数据高效”。 而由于CPU和GPU无法充分利用向量化,随机梯度下降并不特别“计算高效”。 这暗示了两者之间可能有折中方案,这便涉及到小批量随机梯度下降(minibatch gradient descent)。
- 计算单样本的梯度很难完全利用硬件资源!
- 随机采样一个批量大小为n的样本子集,算梯度,对于这个batch都算,然后均一下。充分利用资源!
- 无偏的近似,没有问题。但是降低了方差!(减少了抖动性)
向量化和缓存
- 参考向量化和缓存
小批量
- 处理单个观测值需要我们执行许多单一矩阵-矢量(甚至矢量-矢量)乘法,这耗费相当大,而且对应深度学习框架也要巨大的开销。 这既适用于计算梯度以更新参数时,也适用于用神经网络预测。 也就是说,每当我们执行$\mathbf{w} \leftarrow \mathbf{w} - \eta_t \mathbf{g}_t$时,消耗巨大。其中
$$
\mathbf{g}t = \partial{\mathbf{w}} f(\mathbf{x}_{t}, \mathbf{w}).
$$
- 我们可以通过将其应用于一个小批量观测值来提高此操作的计算效率。 也就是说,我们将梯度$\mathbf{g}_t$替换为一个小批量而不是单个观测值
$$
\mathbf{g}t = \partial{\mathbf{w}} \frac{1}{|\mathcal{B}t|} \sum{i \in \mathcal{B}t} f(\mathbf{x}{i}, \mathbf{w}).
$$
我们看看这对$g_t$的统计属性有什么影响:由于$x_t$和小批量$B_t$的所有元素都是从训练集中随机抽出的,因此梯度的期望保持不变。 另一方面,方差显著降低。 由于小批量梯度由正在被平均计算的$b := |\mathcal{B}_t|$个独立梯度组成,其标准差降低了$b^{-\frac{1}{2}}$。 这本身就是一件好事,因为这意味着更新与完整的梯度更接近了。
- 直观来说,这表明选择大型的小批量$B_t$将是普遍可行的。 然而,经过一段时间后,与计算代价的线性增长相比,标准差的额外减少是微乎其微的。 在实践中我们选择一个足够大的小批量,它可以提供良好的计算效率同时仍适合GPU的内存。
代码实现
- 请参考diy小批量随机梯度下降
动量法(Momentum)
- 使用平滑过的梯度进行更新,使得梯度更新的时候,抖动不要太大!(维护一个惯性,让方向不要改变的过快!)
基本所有的SGD实现都实现了,使用的时候,指定Momentum这个参数的值就可以!!!
Adam算法
- 非常非常非常平滑的SGD,对于学习率没有那么敏感!
其他
- 中间还有AdaGrad算法,RMSProp算法,Adadelta和学习率调节器,可以看看chapter optimization d2l














