sklearn相关算法学习

本文最后更新于：3 年前

这一部分是机器学习初识，里面挺多的内容如缺失值处理，PCA处理之类的技巧，对于美赛很有帮助，有兴趣的小伙伴儿可以看看，相应的教程为bilibili中菜菜的sklearn课堂

机器学习sklearn包

决策树

  1. 如何找出最佳结点和最佳分支
  2. 如何使得决策树停止生长，防止过拟合

分类：

  • 分类树
  • 回归树
  • 画圈专用
  • 高随机版本的分类树
  • 高随机版本的回归树

使用流程：

  1. 实例化，建立评估模型对象
  2. 通过模型接口训练模型
  3. 通过模型接口提取所需要的信息

DecisionTreeClassifier:

  1. 不纯度：选出最佳结点和最佳分枝的方法，叫做不纯度，通常来说，不纯度越低，对于训练集的拟合效果越好，算法就是集中在某个与不纯度相关指标的最优化上。叶子结点的不纯度一定是最低的。
  2. Criterion这个参数就是用来觉得不纯度的计算方法，提供了两种方法，Entropy是信息熵，gini是基尼系数。Criterion对于不纯度更加敏感，对于不纯度惩罚最强，但是使用基本和gini是相同的，信息熵会算的更慢一点。总共就着两种可选嗷。
  3. 决策树的流程：
    1. 计算全部特征的不纯度指标
    2. 选取不纯度最优的特征来分支
    3. 在第一个特征下，再去机选全部特征的不纯度
    4. 循环…
    5. 没有特征可用或者不纯度指标最优，就会停止生长。
  4. 重要参数：
    1. criterion
    2. random_state - 本质为设置随机种子，调参常用
    3. splitter - 选取特征方式不一样，只有best和random两种，详情看代码嗷！！！

剪枝：

  • 过拟合，训练集表现很好，测试集上表现糟糕

  • 如果两者都好，就说明模型以及很棒了。

  • 剪枝对于决策树的影响巨大，正确的剪枝策略是优化决策树算法的核心，sklearn为我们提供了不同的剪枝策略：

    • max_depth 超过设定深度的数值全部剪掉，决策树多一层，对于样本的要求就会多一倍，限制树的深度可以有效限制过拟合，在集成算法使用。实际应用建议从3开始，看看效果如何。这个最最最常用嗷！！！
    • min_samples_leaf和min_samples_split，

    min_samples_leaf保证，每个结点包含的样本个数都最少为min_samples_leaf，一般从五开始使用

    min_samples_split保证，每个结点必须包含至少min_samples_split个样本，这个样本才允许被分支

    • max_features和min_impurity_decrease

    max_features限制分枝时考虑的特征个数，限制过拟合

    min_impurity_decrease限制信息增益大小。本质为父节点的信息熵减去子节点的信息熵，越大表示越有效。

    • 一般使用：最大深度加上后两个中的其中一个。

  • 确定最优的剪枝参数：

    • 超参数的曲线：本质一超参数的取值为横坐标，模型的度量指标为纵坐标的曲线，是用来衡量不同超参数取值下的模型的表现的线。画图永远的神！！！通过score接口来对于学习率和参数的关系，借助于for循环搞出来然后画图嗷！！！

  • 目标权重参数（自己去看）

  • 重要的属性和接口：

    • apply返回每个测试样本所在叶子结点的索引
    • predict返回每个测试样本的回归结果

随机森林

概念：

集成学习，不是单独的机器学习算法，是通过在数据上构建多个模型，集成所有模型的结果。

目标:

考虑多个评估器的建模结果，汇总之后得到了一个综合的结果，以此来获得比单个模型更好的回归或者分类表现。

  • 多个模型集成成为的模型叫做集成评估器，有三类集成算法：袋装法(bagging)，提升法(boosting)和stacking。随机森林是bagging

思想：

构建多个相互独立的评估器。取样，建模，取样，建模反复进行。然后对于预测进行平均或者多数表决原则来决定集成评估器的结果，装袋法的基本模型就是随机森林。随机森林的基分类器就是决策树。

boosting中，则是基选择器是相互关联的，通过不同选择器之间的联系来构建模型。通过结合弱评估器的力量一次次对于难以评估的样本进行云测，从而构成强评估器。代表算法为Adaboost和梯度提升树。

  • sklearn中集成算法模块: ensemble ， 里面有好多好多好多集成算法。很多都是以决策树为核心的集成模型。
  • 分类树的不纯度用基尼系数或者信息熵来衡量，回归树的不纯度用MSE均方差来衡量。
  • score是用来衡量accuracy的接口，几乎每个模型都会用上。

基本建模流程：

image-20210122195945252

随机森林参数：

和决策树相同的参数都是一样的嗷，只是作用域是随机森林中的所有树。

  • max_features：限制分枝时考虑的特征个数，超过个数的特征都会被抛弃，默认值为个数开平方取整。
  • 单个决策树的准确率越高，随机森林的准确率就越高
  • n_estimators：决策树的数量，即基评估器的数量。它越大效果往往越好！！！这个是调参重点，需要找到一个平衡。

重要属性及接口：

  • .feature_importances_返回各个特征重要性
  • .estimators_返回森林的列表
  • .oob_score_袋外得分（有放回随机抽样），会有数据从来没有被抽到，oob为(out of bag)，这些数据也可以不被浪费哦，单独拿来被使用嗷！这个属性可以用袋外数据来测试模型，测试的结果由这个来导出，也能导出模型的精确度。
  • predict_proba，可以返回每个样本对应的分到每一类标签的概率。
  • Random Forest中使用平均每个样本对应的predict_proba返回的概率，求得一个平均的概率，从而决定测试样本的分类

调参

基本思想：

  1. 找目标：

    提升模型的某个评估指标（例如准确率）

    衡量模型在未知数据上的准确率的指标，叫做泛化误差(Genelization error)。当数据在未知数据上表现很糟糕的时候，我们就说模型的泛化程度不够。本质就是测试集表现很烂，和模型的结构有关。

    image-20210123193839922

    目标就是找到最佳模型复杂度。

    对于树来说，最大深度就和复杂度有关呀，树层数越多，就越位于右边。树模型是天生位于图的右上方的模型，天生很容易过拟合。

    参数应该在于减少模型的复杂度

    调参不是一定的，我们应该先判断，模型位于最佳复杂度的哪一边。原理很复杂方差 vs 偏差

    总结四个大点：

    1. 太复杂，太简单，都会使得泛化误差高，我们追求中间的平衡点
    2. 太复杂过拟合，太简单欠拟合
    3. 对于树模型或者树的集成模型，深度越深，枝叶越多，模型越复杂
    4. 对于树或者树的集成模型的目标，很大程度上都是减少模型的复杂度，把模型往图像的左边移动。

    image-20210123201201362

  • 如果模型处于左边如何往右调？只有一个参数也就是max_features可以使得模型往右推
  • 同理也有：如果尝试模型往左推或者往右推都下降，说明模型已经到最低点了。

网格搜索和参数书写：

  • 有一些参数没有参照，很难说清范围，这个时候我们使用学习曲线，逐渐缩小区间再跑曲线

    ![image-20210124100007901](C:\Users\Alexander Liu\AppData\Roaming\Typora\typora-user-images\image-20210124100007901.png)

  • 有一些参数知道取值，或者随着取值变化，整体准确率会如何变化，这个时候可以直接跑网格索搜（本质就是一个一个试嘛哈哈哈哈，只是这个东西有一些约束条件已知。）

    image-20210124100232077

一些技巧：

  • 调参的时候都是从影响最大的开始，往影响最小的开始调。
    1. n_estimators，无论如何先走这一步
    2. max_depth，通过max_depth判断位于模型的哪一边
    3. 然后再对于其他参数进行调整

数据预处理和特征工程

以下的操作全都是再处理数据，别晕了，处理完之后，再挑出来标签类，然后进行类似的处理。

五大流程：

  1. 获取数据
  2. 数据预处理
  3. 特征工程
  4. 建模
  5. 上线

常用的库：

  • preprocessing: 几乎包含所有预处理的内容
  • impute: 填补缺失值专用
  • feature_selection: 包含特征选择的各种方法的实践
  • decompositon: 降维算法

数据预处理：

  • 数据归一化:

$$
X^* = \frac{X - X_{min}}{X_{max}-X_{min}}
$$

​ 归一化是normalization ， 不是正则化，归一化是预处理，正则化不是。

  • 数据标准化： 就是离散中学习的，将数据变成标准正态分布
  • 两者使用范围：
    • 大多选择标准化，因为归一化对于异常值异常敏感。
    • MinMaxScaler在不涉及距离度量，梯度和协方差计算以及数据要被压缩到特定区间时，使用广泛。
    • 建议先试试标准化，不好用换归一化
  • 无量纲化的过程还有好多对应的类，菜菜的pdf中由详细解释嗷。

缺失值处理：

  • 主要用pandas

  • pd.readcsv()

  • 里面有个index_col，如果数据里有索引的话，要记得用这个哦，否则会把索引当作数据读出来。

  • 缺失值的填充：

    • impute.SimpleImputer()
    • missing_value: 默认为np.nan
    • strategy: mean , median , most-frequent , constant
    • fill_value , 当strategy为constant时使用
    • copy: 默认为True，会创建特征矩阵的副本

  • data.info()查看数据基本情况

  • ```python

    填补年龄

    Age = data.loc[:,”Age”].values.reshape(-1,1)

    特征矩阵必须二维，通过reshape转换为二维

    Age[:20] #查看前20行

    from sklearn.impute import SimpleImputer
    imp_mean = SimpleInputer()
    imp_median = SimpleInputer(stategy=”median”)
    imp_0 = SimpleInputer(strategy=”constant”,fill_value=0)

    imp_mean = imp_mean.fit_transform(Age)
    imp_median = imp_median.fit_transform(Age)
    imp_0 = imp_0.fit_transform(Age)

    data.loc[:,”Age”] = imp_median

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28

    - 非常重要的，pandas导出的数据有.loc方法，可以用来提取和锁定特定的数据

    - 编码和哑向量：

      - 因为不能为文字，机器学习处理的只能为数字，以此要对于文字信息进行编码处理，将文字类型转换为数值型

      - ```python
        from sklearn.preprocessing import LabelEncoder
        
        y = data.iloc[:,-1] #特殊矩阵必须二维，而标签允许一维
        
        le = LabelEncoder()
        le = le.fit(y)
        label = le.transform(y)
        # 这里将label成功转换为了0,1,2数值型
        le.classes_ #这个属性只有在fit之后才能看到哦
        
        # 可以一步完成，但是这样是看不到属性的
        label = le.fit_transform(y)
        
        le.inverse_transform(label)#使用inverse_transform也可以逆转
        
        data.iloc[:,-1] = label #让标签等于我们处理后的结果
        
        
        极简写法：
        data.iloc[:,-1] = LabelEncoder().fit_transform(data.iloc[:,-1])

    上面是标签专用型

    • 下面是特征专用型
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    from sklearn.preprocessing import OrdinaryEncoder

    data_ = data.copy()

    OrdinalEncoder().fit(data_.iloc[:,1:-1]).categories_

    data_.iloc[:,1:-1] = OrdinalEncoder().fit_transform(data_.iloc[:,1:-1])

    data_.head()

    • sklearn只接受数值型！！！

独热编码，创建哑向量：

  • 将特征转换为向量的时候，忽略了特征之间的属性。必须告诉算法，这两者完全不同，无法计算，这时用到了哑变量

  • from sklearn.preprocessing import OneHotEncoder

X = data.iloc[:,1:-1]
enc = OneHotEncoder(categories='auto').fit(X)
result = enc.transform(X).toaaray()

极致奢华
OneHotEncoder(categories='auto').fit_transform(X).toarray()

enc.inverse_transform(result)#这个也可以还原嗷
enc.get_feature_names()#这个很重要嗷！！！特别是变量非常多的时候

# 为了添加哑变量
newdata = pd.concat([data,pd.DataFrame(result)],axis=1)#将两个表连起来

newdata.drop(["Sex","Embarked"],axis=1,inplace=True)

newdata.columns = ["Age","Survived","Female","Male","Embarked_C","Embarked_Q","Embarked_S"]
#更改列索引

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13

    - pandas.head()方法默认size=5，返回五行的数据

    ### 处理连续型特征，二值化分段：

    ```python
    data_2 = data.copy()

    from sklearn.preprocessing import Binarizer
    X = data_2.iloc[:0].values.reshape(-1,1) #特征最少为二维，因此无论如何处理时转换为二维

    transformer = Binarizer(threshold=30).fit_transform(X)
    data_2.iloc[:0].values = transformer

  • 将连续型变量划分为分类变量的类: KBinsDiscretizer

  • 重要参数：

    • n_bins ， 分箱的个数，默认为5。以此会被运用到导入的所有特征。如果有不同的分箱需求，需要多次导入。
    • encode , 编码方式，默认为”onehot”

    共有”onehot” , “ordinal” , “onehot-dense”三种

    onehot: 返回一个稀疏矩阵，每一列是一个特征中一个类别。

    ordinal: 每个特征的每个箱子都被编码为一个整数，一列是一个特征

    onehot-dense: 哑变量，返回一个密集数组

    • strategy

  • ```python
    from sklearn.preprocessing import KBinsDiscretizer

    X=data.iloc[:,0].values.reshape(-1,1)

    est = KBinsDiscretizer(n_bins=3,encode=”ordinal”,strategy=”uniform”)
    est.fit_transform(X)

    set(est.fit_transform(X).ravel())
    est = KBinsDiscretizer(n_bins=3,encode=”onehot”,strategy=”uniform”)
    est.fit_transform(X).toarray()

    1
    2
    3
    4
    5
    6
    7

      按照排序和你要的方式，来把数据分箱

    ## 逻辑回归

    ### Sigmoid函数：

回归本质也是线性分类器，本质时线性方法
Sigmoid函数本质为所有S型函数

```

$ \frac{1}{1+e^{-z}} $这个东西很有意思，将任意连续型函数压缩到[0,1]之间，Sigmoid函数只是无限趋近于0，1。
$$
g(z) = f(x) = \frac{1}{1+e^{-\theta^{T}x}}
$$
z就是逻辑回归的时候，那一组向量，线性回归的结果。

image-20210125153006311

  • 形似几率$\frac{y(x)}{1-y(x)}$, 对于形似几率取对数，就可以看出结果就是回归方程。
  • logistic regression为对数几率回归。
  • 逻辑回归的优点：
    • 线性拟合关系拟合效果好到发狂。
    • 逻辑回归计算快
    • 返回结果不是0，1。可以以小数形式呈现的类概率的数字。
    • 抗噪音能力强！
  • 本质为返回对数几率的，在线性数据上表现优异的分类器
  • 数学目的：求最优化参数$\theta$的值，并且基于$\theta$和特征矩阵计算出逻辑回归的结果
  • 损失函数是用于评估模型训练的参数在训练集上的拟合结果，损失小，说明拟合程度高，说明参数优秀。只有求解参数目的的函数才有损失函数。这个玩意儿，天生欠拟合，就类似于树天生过拟合一样。
  • 对于逻辑回归中过拟合的控制，通过正则化来实现。
  • 正则化有两种：
    • image-20210125163154665
    • C为超参数，n为方程中特征的总数，也为方程中总的参数。$\theta_{0}$为截距，通常不参与正则化。
    • penalty 和 C
    • L1: solver="liblinear"，L2可以用别的，默认为L2哦
    • C越小的话，1/C越大，对于模型的惩罚也就越重
    • L1 与 L2的区别：
      • L1会将参数压缩为0，本质是特征选择，掌握了参数矩阵的稀疏性。数据量大，维度高。
      • L2只会让参数尽量小
      • 两个换着来看

回归本质：

通过模型选择的方式和方法，去使得损失函数最小。

K-Means聚类算法

无监督学习概念：

只需要特征矩阵，不需要标签y，聚类就是典型代表

可以大幅度的压缩数据量

聚类和分类的区别：

分类人为给了类，根据给定的数据和标签进行学习

分类本质是由数据分出不同的组，机器自己探索各组数据是否有联系。

  • 算法输出不一样：

    分类结果是确定的，分类的优劣是客观的，不是根据业务或算法要求决定。

    聚类出来的结果是没有固定结果的，聚类结果不确定，不一定能反应真实分类，更具不同的业务需求，结果可能好，可能坏，没有客观的评价。

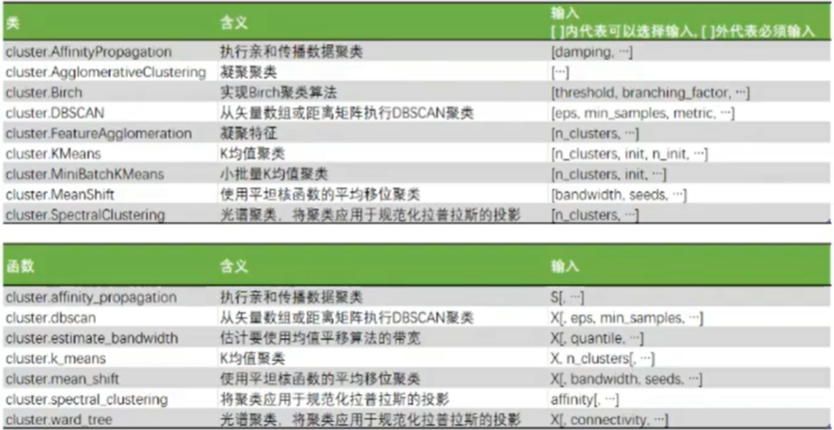
  • image-20210125211814566

K-Means:

  • K-Means算法将一组N个样本的特征矩阵X划分为k个无交集的簇，直观上簇是一组一组聚集在一起的数据，一个簇中就认为是同一类，簇就是结果表示。

![image-20210126105126519](C:\Users\Alexander Liu\AppData\Roaming\Typora\typora-user-images\image-20210126105126519.png)

  • K这个参数是我们用来决定簇的数量
  • 损失函数只有在求解参数的时候才会有的，本质是用来衡量模型的拟合效果的，通过使得损失函数的值最小，求解参数。
  • accuracy用于衡量分类效果的指标准确度，不能最小化accuracy来求解某个模型中需要的信息。因此决策树啊，knn啊，是没有损失函数的
  • ![image-20210126112402394](C:\Users\Alexander Liu\AppData\Roaming\Typora\typora-user-images\image-20210126112402394.png)

评价指标：

  • 想法：

    聚类的目标是确保：簇内差异小，簇外差异大。

  • inertia不适合作为指标，第一，没有大小的明确标准，第二，当数据量比较大的时候，要花很长的时间来进行计算。第三，有交互，圆环之类的效果都很差，只有独立一簇一簇的比较好用。

  • 轮廓系数才是我们用于衡量的指标。

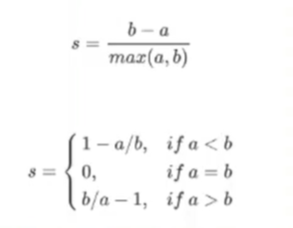
image-20210126153943426

  • 同时比较簇内元素的相似度，和簇之间元素的差异度这两件事儿。范围为(-1,1)
  • 卡林斯基-哈拉巴斯指数，标签未知时的评估指数

SVM支持向量机

  • 找出超平面（比所在空间小一维的空间）

  • 拥有更大的边际的决策变量，泛化误差更小。

损失函数：

  • w的方向垂直于我们的决策边界
  • SVM第一层理解，本质就是损失函数是如何得到的

决策可视化：

见代码

核函数：

用于寻找能把数据完美分割的超平面

kernel = "linear"这个就是线性核函数，适用于线性分割的情况

不同的情况换不同的核

  • 总共有四类：
    • linear , 线性核( 线性 )
    • poly ， 多项式核( 偏线性 )
    • sigmoid , 双曲正切核( 非线性 )
    • rbf , 高斯径向基( 偏非线性 )

小技巧：

升高维度，可以提供一种思想来把数据用超平面来分割开嗷！

image-20210127094342680

  • 这个表还是蛮重要的，一些参数的调整

  • 比如对于rbf的调整，可以通过反复带入不同的参数来进行调整

  • 支持向量机的网格搜索比较友好，好用嗷！！！

  • 这个东西叫软边界，参数C为惩罚项，针对少部分错的数据的调节。

    image-20210127103345932

多元线性回归

参数含义：

image-20210127110749899

  • 线性回归几乎无法调优，内部的计算都已经完成，如果想要调优请参考别的模型，这个不就是概率论里面学的那个鬼东西嘛orz

模型评估指标：

    1. 是否预测了正确的数值，例如 ( RSS，但是这个参数有缺陷，没有明显的衡量指标，就是数据本身的MSE究竟是多少才算拟合效果好呢？其实是没有明确的指标的。）

    我们这儿模型中还有一个比较好的指标叫做均方误差, MSE，这个玩意儿在RSS的基础上除掉了样本数量。

    1. 是否拟合到了足够的信息

  • 调用详情见代码

几个大坑：

  1. 均方误差为负？？？是损失的衡量，凡是带有损失含义的指标，都是负数。真正的均方误差应该为它去掉负号。
  2. 相同的评估指标，不同的结果。分类和回归的算法不同所带来的坑。这里就是输入的，建议查看下模型中的各个参数填的究竟是什么，同一个方法再不同的模型底下参数顺序可能不一样的嗷。
  3. R的平方可以是负的，自己去看原理和逻辑。

朴素贝叶斯

原理：

本质都只是类概率，或者是置信度，不是真正的概率。

置信度和真正的概率有挺大的区别的。朴素贝叶斯是为了用上真正的概率的。

朴素贝叶斯是根正苗红的概率论与数理统计的内容。

贝叶斯是一个不建模的算法（有监督但是不建模）

小技巧与贝叶斯的小特点：

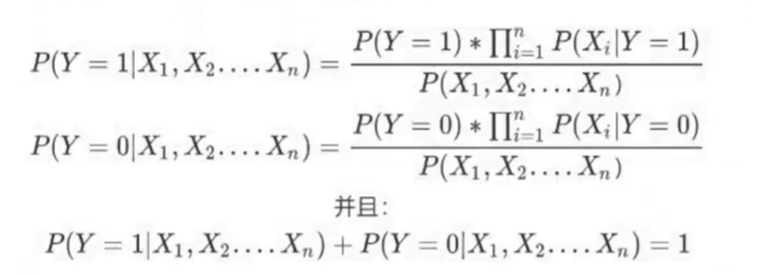
image-20210127215007977

  • 这里取巧了，因为分母的计算量非常大。我们比较分子的大小，哪个大我们就认为最终出现的结果是啥。(MAP)

  • 本质上假设各个特征之间是相互独立的，简化计算过程，就非常的朴素orz，因此叫朴素贝叶斯。也因此，朴素贝叶斯挺不准的orz。

  • 数据数量一般要求比特征数量要多嗷！！！

  • 贝叶斯不好调优

  • 贝叶斯分类

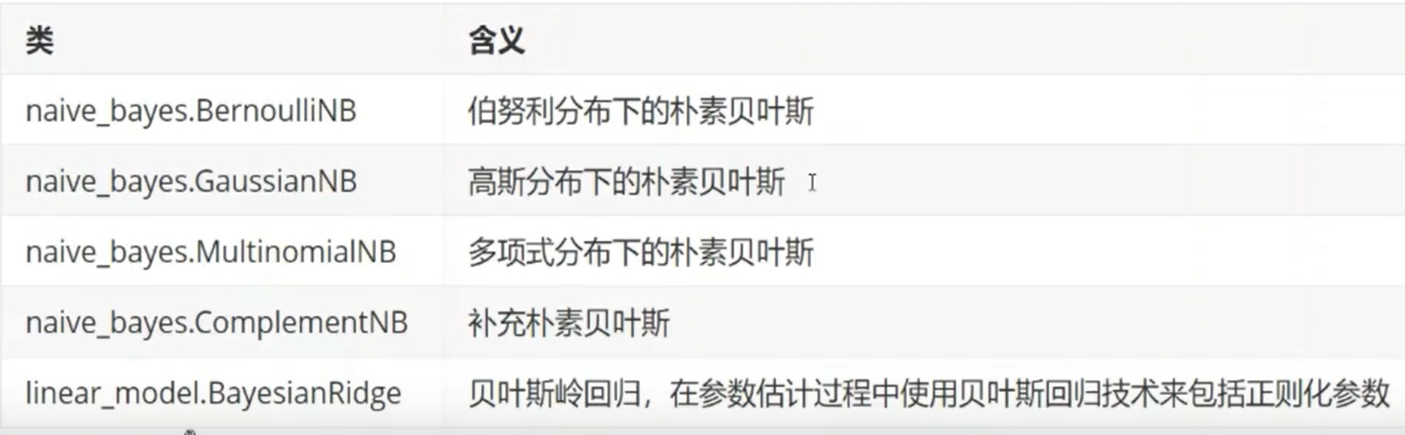
    image-20210130220857876

2021年美赛 > Python
#Python #美赛 #机器学习
sklearn相关算法学习
https://alexanderliu-creator.github.io/2021/02/20/sklearn-zi-xue/
作者
Alexander Liu
发布于
2021年2月20日
许可协议